The 3n+1 Problem
© January 2020, Darrell Cox (A link to "Fermat's Last Theorem and Related Problems"
is at fermat and a link to "Farey Series and the
Riemann Hypothesis" is at riemann. An
article discussing generalized dead limbs is at deadlimb. Other
links are given at the end of this article.)The 3n+1 problem appears to have been first posed
by Collatz in 1937. In this problem, a sequence is generated starting with
an initial natural number n. The rule for generating the next natural number in the sequence is; if
n is even, the next natural number in the sequence is n/2, or if
n is odd, the
next natural number in the sequence is 3n+1. For example, if the
initial value of n is 17, the sequence generated is {17, 52, 26, 13, 40, 20, 10, 5, 16,
8, 4, 2, 1, 4, 2, 1, ...}. If the natural number 4 is
encountered in the sequence, the sequence starts repeating ({4,
2, 1} is generated over and over). There are three possibilities; (1) the
natural number 4 is encountered in the sequence, (2) the sequence starts
repeating, but for a different cycle than {4, 2, 1}, or (3) the sequence
doesn't repeat (in which case the natural numbers generated in the sequence have
to keep getting larger and larger). The 3n+1 conjecture states that only
the first possibility can occur. Let c be an odd integer greater than or
equal to -1 that is not divisible by 3. The next number in the 3n+c
sequence is defined to be 3n+c if n is odd, or n/2 if n
is even (the next number
in the sequence is always a natural number). The sequence
repeats for {4c, 2c, c} if c>-1 or
{2, 1} if c=-1. In
this more general sequence, there are usually cycles other than {4c,
2c,
c}. Although the 3n+1 and 3n-1 sequences have some
unique properties, the 3n+c problem is essentially the same for all c
values.
The 3n+1 problem is difficult and is not likely to be solvable by an
amateur. Although it might seem that the problem should be classified as
"recreational" mathematics, there is a considerable body of mainstream
mathematical literature on the subject. (See Jeffrey C. Lagarias' "The 3x+1
problem: An annotated bibliography (1963-1999)" at
http://arxiv.org/abs/math.NT/0309224
and "The 3x+1 Problem: An Annotated Bibliography, II (2000-2009)"
at http://arxiv.org/abs/math.NT/0608208.
Also, see Lagarias' 1985 article "The 3x+1 problem and its
generalizations" at
http://www.cecm.sfu.ca/organics/papers/lagarias/index.html.) This
article reviews some of the highlights of the 3n+1 problem literature
and presents some original research on the matter (in the form of empirically
derived "results"). The level of the presentation is elementary and empirically
derived propositions are specifically identified when practical.
Sometimes entire sections are mostly empirically derived. In these cases,
a statement to that effect is made at the beginning of the section.
Newcomers to the 3n+1 problem are frequently mystified by how the
sequence increases and decreases in a seemingly random fashion, but always
appears to arrive at 1. The fluctuations of the sequence are of little
interest once the probability of the situation is taken into account (whether
there are cycles other than {4, 2, 1} is far more interesting). See the
section "A probabilistic heuristic" in the Wikipedia article at
http://en.wikipedia.org/wiki/Collatz_conjecture for a brief introduction to
the subject, the section "A heuristic argument" in Lagarias' 1985 article for
more details, and the section "A Random-Walk Argument" in Richard E. Crandall's1
1978 article "On the "3x+1" Problem". The probabilistic argument to be given here avoids the "mixing" assumptions in
other approaches and is amenable to empirical verification. If the 3n+1
sequence is bounded and there are no cycles other than {4, 2, 1}, then the
sequence element 1 must eventually be reached. The argument to be given is
then that the 3n+1 sequence is bounded.
A Probabilistic Argument that the 3n+1 Sequence is Bounded
The probabilistic argument entails a restructuring of the Collatz graph and
an alternate definition of the 3n+1 sequence. The Collatz graph is a tree-like structure that shows how the sequence
element 1 can be arrived at starting from different initial n values.
(See the Wikipedia article for the standard depiction of the Collatz graph.
Of course, the graph can only be constructed if the 3n+1 conjecture is
assumed to be true.) When
n is even and n-1 is divisible by 3, there is a node in the graph where the
previous elements in the sequence are 2n and (n-1)/3. For example, in the Collatz graph, two limbs ending in 32 and 5 converge to form a limb starting at
16. In the restructured Collatz graph, 5 is considered to be a
continuation of the limb segment starting with 16. In general, (n-1)/3 is
considered to be a continuation of the limb segment at such nodes. (That
is, "odd" paths are taken when tracing back through the nodes.) The
limbs in the restructured Collatz graph are then;
{4, 2, 1}
{..., 24, 12, 6, 3, 10, 5, 16, 8}
{..., 72, 36, 18, 9, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20}
{..., 120, 60, 30, 15, 46, 23, 70, 35, 106, 53, 160, 80}
{..., 168, 84, 42, 21, 64, 32}
.
.
.Each limb other than (4, 2, 1) contains exactly one odd
element divisible by 3. Let j denote the odd natural number that is
divisible by 3. The natural numbers to the right of j are not divisible by
3 (since 3 does not divide 3j+1, (3j+1)/2, ...). The natural numbers to
the left of j must be of the form 2ij where i is a natural number
(no natural number can attach to this part of the limb since 3 does not divide
2j-1, 4j-1, 8j-1, ...). (The limbs listed above [starting with the second
limb] contain 3, 9, 15, and 21 respectively. The second limb attaches to
the first limb, the third and fifth limbs attach to the second limb, and the
fourth limb attaches to the third limb.) Note that other than the limb {4,
2, 1}, the next-to-last element in a limb is divisible by 8 and that no natural
number to the right of the odd natural number divisible by 3 and before the
next-to-last natural number is divisible by 8 (this is known as a 1-2 sequence
vector since there are either one or two even sequence elements between
successive odd sequence elements).
The 3n+c sequence can
be defined by the recurrence operation [(3/2)h(n+c)-c]/2→n, 2h
divides n+c, 2h+1 does not divide n+c. Each iteration of the
recurrence operation starting with an odd element will be referred to as a "jump". If n is
odd and 22 does not divide n+c, then the sequence {n, 3n+c,
(3n+c)/2=(3/2)(n+c)-c, ...} is generated where every other element of the
sequence up to (3/2)(n+c)-c is odd. Similarly, if
n is odd and 22
divides n+c, 23 does not divide n+c, then the sequence
{n, 3n+c,
(3n+c)/2, 3[(3n+c)/2]+c, [3[(3n+c)/2]+c]/2=(3/2)2(n+c)-c, ...} is
generated where every other element of the sequence up to (3/2)2(n+c)-c
is odd. In general, if 2h divides n+c, 2h+1 does not
divide n+c, then the first element in the sequence that is divisible by 4 is the
one just before (3/2)h(n+c)-c. If [(3/2)h(n+c)-c]/2
is even, then the first element in the sequence that is divisible by 8 has been
found. Each limb of the restructured Collatz graph other than {4, 2, 1}
consists of a series of jumps, the last jump ending in an even natural number
(which connects the limb to the rest of the tree). The question of whether
the 3n+1 sequence (or the 3n+c sequence) is bounded then reduces to the question
of whether there are any jumps ending in an even natural number. The
distribution of the number of jumps (denoted by i) before an even natural number
is reached for the 1000000 sequences starting with 3, 9, 15, ..., 5999997 is;
i=1, 500002
i=2, 250004
i=3, 124998
i=4, 62498
i=5, 31211
i=6, 15683
i=7, 7782
i=8, 3897
i=9, 2000
i=10, 972
i=11, 497
i=12, 230
i=13, 109
i=14, 58
i=15, 23
i=16, 13
i=17, 15
i=18, 3
i=19, 3
i=20, 0
i=21, 1
i=22, 0
i=23, 0
i=24, 1The probability that i iterations are required is about (1/2)i. Even though the probability that the sequence is unbounded is effectively 0,
it's unlikely that this part of the 3n+1 conjecture is provable.
(The data indicates that the process which forms 3n+1 sequences [having
1-2 sequence vectors] consisting of an arbitrarily large number of jumps is
random. [In the mathematical literature, such processes are usually said
to be "pseudo-random", but in the absence of a rigorous definition of "random",
one could argue that saying the process is random is acceptable.]). The
probability that h=1 is about 1/2, the probability that h=2 is
about 1/4, the probability that h=3 is about 1/8, etc. These are
the expected probabilities. Even if such a limb (one having a 1-2 sequence
vector starting with an odd natural number divisible by 3) attaches to another
such limb, and that limb attaches to another such limb, etc., there is no
guarantee that the trunk of (4, 2, 1) would be reached. The 3n+1
sequence may then be unbounded in this way. About 90% of the time, the odd
natural number divisible by 3 in a limb that attaches to another limb is larger
than the odd natural number divisible by 3 in that limb. (The proportions
for the first 10, 100, 1000, 10000, 100000, 10000000, and 10000000 odd natural
numbers divisible by 3 are 0.9, 0.91, 0.905, 0.9022, 0.90333, 0.903506, and
0.903254 respectively. The limb (..., 24, 12, 6, 3, 10, 5, 16, 8) doesn't
attach to another limb containing an odd natural number divisible by 3, but this
is still counted as if 3 were greater than an odd natural number divisible by 3
in another limb.) There is then a strong tendency for the limbs to
eventually be attached to the trunk.
If c=1 and negative n values are allowed, the absolute value of
the integer divisible by 3 in a limb that attaches to another limb is larger
than the absolute value of the odd integer divisible by 3 in that limb about 90%
of the time. Also, the probabilities for the number of jumps required to
reach an even integer starting with an odd integer divisible by 3 are the same as
when only positive n values are allowed. If c>1
and negative n values are allowed, the same probabilities apply.
Let t denote the odd integer divisible by 3. For example, for c=5,
5 does not divide t, -10k≤(t-3)/6≤10k,
and
k=1, 2, 3, ..., 7, the proportions are 0.941176, 0.913043, 0.906933,
0.903944, 0.903457, 0.903540, and 0.903280 respectively.
For k=4, a histogram of the differences in absolute values of
t values divided by 1536 (to scale the values) is;

For c=1 and k=4, a histogram of the differences in absolute
values of t values divided by 1536 is;

(There are fewer values for c=5 due to excluding t values
divisible by 5.) In general, 8/9 appears to be a lower bound of these proportions.
In 1972, John H. Conway2 showed that a more general function
iteration problem similar in form to the 3n+1 problem is computationally
undecidable. This lends some credence to the notion that this part of the
3n+1 problem is unprovable. However, some progress can be made in
this area; in 1976, Riho Terras3 showed that almost all numbers have
finite "stopping time". Let S0=N and Si=Si-1/2
if Si-1 is even or 3(Si-1+1)/2
otherwise. (This is the way the 3n+1 sequence is usually defined in
the mathematical literature. This turns out to be the "natural" way to
define the sequence.) The smallest value of i such that Si<S0
is defined to be the stopping time of N.
Necessary and Sufficient Conditions for Cycles in the 3n+c Sequence to Exist
An element s in the 3n+c sequence can be expressed as (Xa-cZ)/Y where
a is a
subsequent element in the sequence, X is a natural number and a power of 2
(X equals 2l where l is the length of the
sequence [where the element after an odd element i is defined to be (3i+c)/2]),
Y is
a natural number and a power of 3 (Y equals 3m where
m is the number of odd elements in the sequence), and Z is a natural number and a 3-adic number
with power-of-two coefficients (see Bohm and Sontacchi's4 article and page 41 of Gunther Wirsching's5
book [for discussions of the c=1 case] ). (An example of Z is
2233+2332+2531+2630
=340. A formula for Z will be given later.)
If s=a, then s=cZ/(X-Y). Other than setting
c to X-Y, no method for finding X, Y, and Z where
cZ/(X-Y)
is an integer is known, so other requirements for cycles will be investigated.
The 3n+c Sequence in the Integer Domain
In the mathematical literature, the cycles {4, 2, 1} for c=1
and {2, 1} for c=-1 are usually said to be "trivial" (but there doesn't
appear to be any rationale for this designation). For a given c
value, there appear to be few (if any) non-trivial cycles.
When c is composite, some of the cycles that occur are essentially no
different from the cycles that occur for a factor of c (the elements of the
cycle are just a common multiple of the elements of the cycle for the factor of
c). (Cycles that are not multiples of other cycles are said to be
primitive. Note that the cycle {4c, 2c, c} for c>1
is not primitive.) Also, some cycles for a given c value are interrelated; they
have the same lengths (number of elements) and the same number of odd elements (and approximately the same dynamic
range of elements). Counting these types of cycles as redundant, a histogram
of the apparent number of cycles (including the "trivial" cycles) for c values less than or equal to 151 is;
number of cycles
number of c values
0 0
1 20
2
21
3 10
4
1
5 0
6 0
total=52
A Poisson probability distribution with a parameter of 1 can be used to model
the number of 3n+c cycles for a given c value (see the author's
"The 3n+1 Problem: A Probabilistic Approach" at
http://www.cs.uwaterloo.ca/journals/JIS/VOL15/Cox/cox10.pdf).
Associated cycles are defined in the Journal of Integer Sequences
article. A Poisson probability distribution with a parameter of 1.082
superimposed on a histogram of the number of cycles for a given
c value (allowing negative n values and counting only one of
interrelated or associated cycles) for c values greater than 0 and less than or equal to
19999 is;

(The mean of the actual distribution is 1.082.)
A Poisson probability distribution with a parameter of 1.070 superimposed on a
histogram of the number of cycles for a given c value (allowing negative
n values and counting only one of interrelated or
associated cycles) for c values greater than 0 and less than or equal to
29999 is;

When c=-1, there are two known cycles other than (2, 1); the cycle (20, 10, 5, 14,
7) and the cycle (68, 34, 17, 50, 25, 74, 37, 110, 55, 164, 82, 41, 122, 61, 182,
91, 272, 136). A frequently asked question is why there are non-trivial
cycles for the 3n-1 sequence, but apparently not for the 3n+1
sequence. There are many such examples when general negative c
values are allowed. For example, there is at least one primitive cycle for
the 3n+7 sequence, but apparently none for the 3n-7 sequence.
However, there appears to be at least one primitive cycle in either the 3n+c
sequence or the 3n-c sequence. This indicates that the
distinction between the 3n+c and 3n-c sequences is
artificial and that negative n values should be allowed (and that the
c values should be required to be positive). (However, it is sometimes
convenient to use the original definition of the 3n+c sequence.)
More evidence that the 3n+1 and 3n-1 sequences (n>0) should
be considered to be the same sequence will be presented later.
Interrelated 3n+c Cycles
In this section, negative n values are allowed, c is required to
be positive, and the element after an odd element i in the 3n+c
sequence is defined to be (3i+c)/2. A parity vector gives
the order of even and odd elements in a 3n+c sequence, a "'1" for an odd
element and a "0" for an even element. Let k0, k1,
k2, ..., km-1 denote the positions
of the 1's in a parity vector containing m 1's and having a length of
l. Let Z denote 3m-12k(0)+3m-22k(1)+3m-32k(2)+...+302k(m-1)
(due to typographical difficulties, k(0), k(1), k(2), ...,
k(m-1) is used to denote k0, k1,
k2, ..., km-1). A cycle
exists if and only if cZ/(2l-3m) is
an integer. (Note that every parity vector containing at least one 1
corresponds to a cycle for some c value [duplicated parity sub-vectors
correspond to duplicated sub-cycles].) For example, for the c=17
cycle of (2, 1, 10, 5, 16, 8, 4), k0=1 and k1=3,
Z=3121+3023=14, 119=27-32,
and (17·14)/119 is an integer. There do not appear to
be any factors of c left over after the division by 2l-3m.
This has been confirmed experimentally (for the 73916 distinct (c, l,
m) values of the 3n+c cycles for c<100000):
(1) A 3n+c cycle exists only if c divides 2l-3m.
If this proposition holds, Z need not be considered when searching for
cycles; only the factors of 2l-3m need be
considered. When c=|2l-3m|, an
arbitrarily constructed parity vector with a length of l and containing
m 1's corresponds to a cycle (or possibly duplicated sub-cycles if l
and m are not relatively prime), but the cycle is not guaranteed to be
primitive. When reduced, such a cycle corresponds to a cycle for a c
value that is a proper divisor of 2l-3m.
In this sense, there is no problem of finding cycles; they're all well-defined
and determined by the parity vectors. Even the number of interrelated
cycles is determined by the combinatorics of generating parity vectors that are
distinct under rotation (see the above Journal of Integer Sequences
article for a table of the numbers of distinct parity vectors for l less
than or equal to 20 and m less than or equal to 10). There is,
however, the problem of determining which c values the primitive cycles
map to. For example, for l=1 and m=1, the
parity vector is (1) (corresponding to the cycle {-1} for c=1), for l=2
and m=1, the parity vector is (0, 1) (corresponding to the cycle {2, 1}
for c=1), and for l=3 and m=2 the parity vector is (1, 1,
0) (corresponding to the cycle {-5, -7, -10} for c=1). For l=11
and m=7, there are 30 distinct parity vectors, the first few of which are
(0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0), (1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0), (1, 1, 0,
1, 0, 1, 1, 1, 1, 0, 0), ... (corresponding to cycles for c=139).
The cycle corresponding to the first parity vector is not primitive (when c=139)
and corresponds to the remaining known c=1 cycle of {-34, -17, -25, -37,
-55, -82, -41, -61, -91, -136, -68}.
Another example factorization will be given. For l=8 and m=4,
the distinct parity vectors are (1, 1, 0, 0, 1, 1, 0, 0), (0, 1, 0, 1, 0, 1, 0,
1), (1, 0, 1, 1, 0, 1, 0, 0), (0, 0, 1, 1, 1, 1, 0,
0), (0, 1, 1, 0, 1, 1, 0, 0), (1, 0, 0, 1, 1, 1, 0, 0), (0, 1, 0, 1, 1, 1, 0,
0), (1, 0, 1, 0, 1, 1, 0, 0), (1, 1, 0, 1, 0, 1, 0, 0), and (0, 1, 1, 1, 0, 1,
0, 0) (corresponding to cycles for c=175). The first parity
vector corresponds to two duplicated primitive cycles for c=7, the second
parity vector corresponds to four duplicated primitive cycles for c=1, the third parity vector
corresponds to a primitive cycle for c=25, the fourth and fifth parity vectors
correspond to primitive cycles for c=35, and the remaining parity vectors
correspond to primitive cycles for c=175. Although 5 also
divides 175, there are no primitive cycles for this c value when l=8
and m=4 (the parity vectors have been used up by cycles for the larger c
values and c=1).
Apparently, every c value is covered in this mapping. A more
appropriate question to ask than why cycles don't exist for a given c
value is why they do exist and what the expected number of cycles is (see the
Journal of Integer Sequences article for more details).
(For a given c value, two primitive cycles cannot have the same parity
vector. For example, the 3n+5 sequence 83, 254, 127, 386, 193, 584,
292, 146, and 73 has the same parity vector as the 3n+5 cycle 19, 62, 31,
98, 49, 152, 76, 38, and 19. The ratios of the corresponding odd elements
decrease monotonically and are 4.368, 4.097, 3.939, and 3.842. More
generally, a primitive 3n+c1 cycle cannot have the same
parity vector as a primitive 3n+c2 cycle. For
example, the 3n+7 sequence 65, 202, 101, 310, 155, 472, 236, 118, and 59
has the same parity vector as the above 3n+5 cycle, but the ratios of the
corresponding odd elements are 3.421, 3.258, 3.163, and 3.105. The 3n+7
sequence 1, 10, 5, 22, 11, 40, 20, 10, and 5 has the same parity vector as the
above 3n+5 cycle, but the ratios of the corresponding odd elements are
0.053, 0.161, 0.224, and 0.263. For a primitive
3n+c cycle where c≠|2l-3m|,
there is always another cycle [not necessarily primitive] having the same parity
vector where c=|2l-3m|. This
accounts for Proposition (1).)
The Minimum Element in a 3n+c Cycle
In 1997, Halbeisen and Hungerbühler6
proved optimal estimates for the length of a Collatz cycle in terms of its
minimum using the formula Ml,m=∑(]jm/l[
- ](j-1)m/l[)2j-13m-]jm/l[
where the summation is from j=1 to l and the reversed brackets
denote the ceiling function (the minimum is Ml,m/(2l-3m)). For a Collatz cycle, Ml,m/(2l-3m)
is larger than the minimum element in other cycles having a length of l
and containing m odd elements. Their Lemma 4
is;
Let s = (s1,..., sl)
and t = (t1,..., tl) be two distinct
elements of Sl,n. If ∑ki=1
si ≤ ∑ki=1
ti for all k an element of {1,..., l}, then φ(s)
> φ(t).
Sl,n denotes the set
of all 0-1 sequences of length l containing exactly n ones (the number of
ones is denoted by m in this article). φ is defined
recursively by φ({})=0, φ(s0)=φ(s), φ(s1)=3φ(s)+2l(s)
where s denotes an arbitrary element of S (S denotes the
union of all Sl,n sets from n=0 to l) and
l(s) the length of s. (The explicitly computed form of
φ is denoted by Z is this article.)
For a given s, some left-shift permutation of s (denoted by
t) gives a minimum φ(t) value. For all s an element of Sl,n,
Ml,n is defined to be the maximum of these
minimum φ(t) values. Their Lemma 5
(where the sequence s̃ for which φ attains the value Ml,n
is determined) is;
Let n ≤ l be natural
numbers. Let s̃i = ]in/l[ - ](i -
1)/l[ (for 1≤ i ≤ l). Then φ(s̃) equals
the minimum φ(t) value of s̃ (equal to Ml,n).
(Due to typographical difficulties, the exact form of this lemma is not
duplicated here.) In the proof of this lemma, Lemma 4 is used and ∑ki=1ti is represented by a staircase. For example, a
staircase for s̃ where l=27 and n=17 along with a staircase
representing the partial sums of [in/l]-[(i-1)/l]
where the brackets denote the floor function is;

The staircase using the floor function (not used in the proof of Lemma 5) can be viewed as being an upside-down
staircase where Halbeisen and Hungerbühler's logic
can be used to find a lower bound of the maximum odd element in a Collatz cycle. Let tj=[jm/l]
- [(j-1)m/l], j=1, 2, 3, ..., l.
Let r denote gcd(l, m). The parity vector ]jm/l[ - ](j-1)m/l[,
j=1, 2, 3, ..., l, consists of r identical sub-vectors.
Similarly, the parity vector tj consists of r identical sub-vectors
and each of these sub-vectors is the same as the corresponding sub-vector of ]jm/l[ - ](j-1)m/l[,
j=1, 2, 3, ..., l, except for the first and last elements. First suppose
that l and m are relatively prime. When the parity vector ]jm/l[ - ](j-1)m/l[,
j=1, 2, 3, ..., l, is right-rotated by one position (corresponding to a
multiplication by 2), it matches tj except for the first two elements of each sub-vector. The first mismatch
corresponds to a loss of 3m-1
and the second mismatch corresponds to a gain of 2∙3m-1.
In general, the loss is ∑2i(l/r)3m-1-i(m/r)
where the summation is from i=0 to r-1. Let Nl,m
denote 2Ml,m- ∑2i(l/r)3m-1-i(m/r). An alternate way of
looking at Halbeisen and Hungerbühler's result
is;
(2) If c=|2l-3m| and the elements of the interrelated 3n+c cycles are
positive, Ml,m is greater than or equal
to the minimum elements in the interrelated 3n+c cycles (not
necessarily primitive) and Nl,m is less than or
equal to the maximum odd elements in the interrelated 3n+c cycles. Analogous results apply if the elements of
the cycles are negative. (The sign of the elements of a cycle in the 3n+c sequence
cannot change. The signs of the elements in interrelated 3n+c
cycles are the same [the sign is determined by 2l-3m].)
Also, both Ml,m and Nl,m are in one of these
cycles.
All 3n+c cycles appear to be generated from cycles where c=|2l-3m|.
For example,
when l=11, and m=7, Ml,m=3767, Nl,m=6805
and |2l-3m|=139. By Proposition (2),
3767/139 (approximately equal to 27) must be greater than or equal to the
minimum element in the c=-1 cycle (17) and 6805/139
(approximately equal to 49) must be less than or equal to the maximum
odd element in the c=-1 cycle (91). For the c=-1 cycle of
(5, 7, 10), M3,2=5 and N3,2=7 (-1 equals 23-32).
Note the relevance of the Catalan conjecture
(now Mihăilescu's theorem).
For c=-17, the cycles are (85, 119, 170, 85, 119, 170), (103, 146, 73,
101, 143, 206), and (65, 89, 125, 179, 260, 130). -17 equals 26-34,
M6,4=85, and N6,4=119. 85 is greater than
73 and 65. 119 is less than 143 and 179. The cycle (85, 119, 170) is not
primitive and reduces to the c=-1 cycle. Note that 17 must divide 33+23·3
for this to be possible. For the c=1 cycle of (4, 1), 1 equals 22-31,
and M2,1=N2,1=1. There can be no other
such c=1 cycles. This leaves the possibility of interrelated 3n+c
cycles where one of the cycles is not primitive and reduces to a c=1
cycle.
When l and m are not relatively prime and c=|2l-3m|,
the cycles generated from Ml,m are not primitive
(due to properties of binomial expansions). For example, when c=29-36,
reducing the cycle generated by M9,6 effectively divides 29-36
by (29-36)/(23-32). For l=6, 9,
12, 15, 18, ..., and m=3, 6, 9, 12, 15, ..., there are
0, 0, 1, 2, 3, ..., odd cycle elements between Ml,m
and Nl,m. In this case, c, Ml,m,
and Nl,m have at least one prime factor in
common. The respective prime factors are 37, 7·31, 13·109, 10177, 78697,
.... The respective c values (after reduction) are 1, -1, -11, -49,
-179, ..., and the respective cycles are (1, 2), (5, 7, 10), (19, 23, 29, 38),
(65, 73, 85, 103, 130), and (211, 227, 251, 287, 341, 422), .... Similar results are
obtained for other combinations of l and m. When l and m are relatively prime and c=|2l-3m|,
the cycles generated from Ml,m are primitive.
The largest upper bound of minima in potential 3n+c cycles having the same number of even
elements can also be easily determined. An empirical result is;
(3) Ml,m/|2l-3m|,
l=m+k,
m=1, 2, 3, ...., increases until the sign of 2l-3m
changes and then decreases. More precisely, the maximum Ml,m/|2l-3m|
value occurs immediately before the sign change or at the sign change.
For example, M6,4/|26-34| is greater
than M5,3/|25-33|, 25-33
is positive, and 26-34 is negative (the maximum occurs at
the sign change). M8,5/|28-35| is
greater than M9,6/|29-36|, 28-35
is positive, and 29-36 is negative (the maximum occurs
before the sign change).
The Minimum Element in a 3n+c Cycle and the Continued-Fraction Convergents of
Log(3)/Log(2)
In his 1978 article, Crandall proved a lower bound of 17985 for the number of
odd elements in a 3n+1 cycle (n>0) using the minimum in a
hypothetical cycle and the continued-fraction convergents of log(3)/log(2).
Recent 3n+1 cycle research frequently involves use of the continued-fraction convergents of log(3)/log(2). For some purposes, this is too restrictive;
valuable information is thrown away. This
is the rationale for defining generalized continued-fraction convergents
(allowing less accurate approximations). Let (c, d), (e,
f), and (g, h) denote successive continued-fraction
convergents of a real number and let j denote the ceiling of h/f.
(ei, fi) and (ei+c, fi+d), i=1,
2, 3, ..., j, can be considered to be generalized continued-fraction
convergents of the real number. (Sometimes it is convenient to consider
just (ei+c, fi+d), i=1, 2, 3, ..., j,
to be the generalized continued-fraction convergents of the real number; ei+c
and fi+d are then relatively prime.) The generalized continued-fraction convergents of log(3)/log(2) are
(2, 1), (3, 2), (4, 2), (5, 3), (6, 4), (8, 5),
(9, 6), (11, 7), (16, 10), (19, 12), (24, 15), (27, 17), (38, 24), (46, 29),
(57, 36), (65, 41), (76, 48), (84, 53), .... An empirical result is;
(4) The absolute values of 2l-3m
increase monotonically for (l, m) values that are generalized
continued-fraction convergents of log(3)/log(2) (excluding (2, 1), (4, 2), (6, 4),
and (9, 6)).
The significance of this is that for a given c value, there can be at
most one solution of c=|2l-3m| where
(l, m) are generalized continued-fraction convergents of
log(3)/log(2) (excluding (2, 1), (4, 2), (6, 4), and (9, 6)).
An algorithm for generating the lengths and numbers of odd elements of 3n+1
or 3n-1 (n>0) sequences associated with potential cycles having
1-2 sequence vectors almost always gives the generalized continued-fraction
convergents of log(3)/log(2) (and only these values). The algorithm gives
four (l, m) values that are not generalized continued-fraction
convergents of log(3)/log(2) and four generalized continued-fraction convergents
of log(3)/log(2) are not given. (This algorithm will be
discussed in detail later. See the section "The Minimum in a Collatz
Cycle".) This is more evidence that the generalized
continued-fraction convergents of log(3)/log(2) are of significance to the 3n+1
problem. The continued-fraction convergents of log(3)/log(2) will be
further generalized in the next section.
M-Cycles and an Algorithm for Determining When the Sign of 2l-3m
for a Fixed l-m Value Changes
A cycle with no even elements can occur only if (3/2)i(n+c)-c=n
where n is odd, i<h, and 2h is the largest power of 2 that
divides n+c ((3/2)i(n+c)-c
is an incomplete jump). The only primitive cycle with no even elements is
the cycle {-1} for c=1 (where c=-n). An m-cycle
is a hypothetical cycle in the 3n+1 sequence (n>0) having m local
minima. (In this article, such cycles in the 3n+c sequence
will be referred to as being M-cycles.) In 1977, R. P. Steiner7 proved that 1-cycles can't
exist. A jump in the 3n+c sequence ending in the initial
odd element is analogous to a 1-cycle (there would be exactly one even element
in the cycle). Empirical results are;
(5) A cycle in the 3n+c sequence having only one even
element can occur only if c=|2l-3l-1|.
(6) A cycle in the 3n+c sequence having only one odd element
can occur only if c=|2l-3|.
A successor of a, a>0, in the 3n+c sequence is
greater than a if 3ma>2la-cA (that
is, 3m/2l>1-cA/(2la))
where the values of l, m, and the integer A depend on the
parity vector between a and the successor of a. For a
sufficiently large a, the successor of a is larger than a
if 3m/2l>1. For a sufficiently large initial sequence value a, the
following algorithm generates the parity vector (denoted by p) of a 3n+c
sequence (with positive elements) where twice the minimum element in the
sequence is larger than the maximum odd element in the sequence. Set x
to 1, p1 to 1, and i to 2. Then repeat the
following operations. Set pi to 1, x to (3/2)x,
and increment i. If x>1, set pi to 0, x
to (1/2)x, and increment i. The resulting parity vector is
1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, .... The portion of the
parity vector up to the Mth 0 gives an M-cycle. (The first 1
in the parity vector is taken to follow the 0 so that a cycle is formed.)
The resulting (l, m) values (where l is the number of
elements in the cycle and m is the number of odd elements) for the M-cycles
are (3, 2), (5, 3), (8, 5), (11, 7), (13, 8), (16, 10), (19, 12), (21, 13), (24,
15), (27, 17), (30, 19), (32, 20), (35, 22), (38, 24), (40, 25), (43, 27), (46,
29), (49, 31), (51, 32), (54, 34), (57, 36), (59, 37), (62, 39), (65, 41), (68,
43), (70, 44), (73, 46), (76, 48), (78, 49), (81, 51), (84, 53), ....
Empirical results are;
(7) These (l, m) values include the generalized continued-fraction
convergents of log(3)/log(2) (except for (2, 1), (4, 2), (6, 4), and (9, 6)).
Also, 2m>l.
(8) The
difference in l values of a pair of successive M-cycles is 2 or 3
and the difference in m values is 1 or 2 respectively.
(9) There are either 3 or 4 successive M-cycles where the
difference in l values is 3 (2l-3m is
negative for the third or fourth M-cycle and positive otherwise).
(10) When there are 4
successive M-cycles where the difference in l values is 3, the
values of Ml,m/|2l-3m|
increase up until the third M-cycle and
then decrease. The absolute values of 2l-3m
usually increase, but may decrease for the third M-cycle. When
there are 3 successive M-cycles where the difference in l values
is 3, the values of Ml,m/|2l-3m|
usually increase, but may decrease for
the third M-cycle. The absolute values of 2l-3m
usually increase, but may decrease for the third M-cycle (but only if the
value of Ml,m/|2l-3m|
increases). After the third or fourth
successive M-cycle where the difference in l values is 3, the
value of Ml,m/|2l-3m|
decreases and the absolute value of 2l-3m
increases (the difference in l values is 2).
(11) There are no successive M-cycles where the difference in l
values is 2.
A table of the ]jm/l[ -](j-1)m/l[, j=1,
2, 3, ..., l, values (given in the columns) for (l, m)=(3,
2), (5, 3), (8, 5), ..., (103, 65) is;
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 0 0 1 0 0 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 1 0 1 1 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 0 0 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 1 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 0 0 1 0 0 1 1 0 0 1 0 0 1 1 0 1 1 0 0 1 0 0 1 1 0 1 1
0 1 1 0 1 1 0 0 1 1 0 1 1 0 0 1 0 0 1 1 0 1 1 0 0 1 0 0
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 0 0 1 1 0 1 1 0 1 1 1 0 1 1 0 1 1 0 1 1 1 1 1 1
0 1 1 0 0 1 0 0 1 0 0 0 1 0 0 1 0 0 1 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1
0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 0 0 1 0 0 1 1 0 0 1 0 0 1 0 0 0 1 0 0 1
0 1 1 0 1 1 0 0 1 1 0 1 1 0 1 1 1 0 1 1 0
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 0 0 1 1 0 1 1 0 0 1 0 0 1 1 0 1 1
0 1 1 0 0 1 0 0 1 1 0 1 1 0 0 1 0 0
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 1 0 1 1 0 1 1 0 1 1 1 0 1 1
0 0 1 0 0 1 0 0 1 0 0 0 1 0 0
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 0 0 1 0 0 1 0 0 0 1 0 0 1
0 1 1 0 1 1 0 1 1 1 0 1 1 0
1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 1 0 1 1 0 1 1 1 1 1 1
0 0 1 0 0 1 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1
0 1 0 0 1 0 0 1 1 0 0 1
0 1 1 0 1 1 0 0 1 1 0
1 1 1 1 1 1 1 1 1 1 1
0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1
0 1 1 0 1 1 1 1 1 1
0 0 1 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1
0 1 0 0 1 1 0 1 1
0 1 1 0 0 1 0 0
1 1 1 1 1 1 1 1
0 0 0 0 1 0 0 1
1 1 1 0 1 1 0
0 1 1 1 1 1 1
0 0 0 0 0 0
1 1 1 1 1 1
0 1 1 0 1 1
0 0 1 0 0
1 1 1 1 1
0 1 0 0 1
0 1 1 0
1 1 1 1
0 0 0 0
1 1 1
0 1 1
0 0
1 1
0 1
0
1
0
Note that there are rows of values consisting of all 0's, rows of values
consisting of all 1's, rows of values consisting of all 1's except for an
initial value of 0, and pairs of adjacent rows of values where the element-by-element sum
consists of all 1's (disregarding the first element of the first row). The elements in
one of these pairs of adjacent rows appear to become all 0's or 1's eventually.
Let qj-1=]jm1/l1[
- ](j-1)m1/l1[, j=2, 3, 4,
..., l1, where (l1, m1) is
a generalized continued-fraction convergent of log(3)/log(2), gcd(l1,
m1)=1, and (l1, m1)≥(11,
7). Let l2, l2<l1, denote the number of
elements in an M-cycle generated from the parity vector p and let
rj=qj, j=1, 2, 3, ..., l2.
If l2 is the last of a succession of l values having a difference
of 3, switch the last two elements of r. An empirical result is;
(12) A rotation of r
matches the first l2 elements of the parity vector p
(usually, a right-rotation of 3 suffices).
The absolute values of 2l-3m where (l,
m) are multiples of a continued-fraction convergent (as usually defined)
of log(3)/log(2) increase monotonically since the values of Ml,m/|2l-3m|
are the same.
Truncated Ml,m/(2l-3m)
values corresponding to the generalized continued-fraction convergents of log(3)/log(2)
(excluding the multiples of convergents) are;
l=2, m=1, 1
l=3, m=2, -5
l=5, m=3, 4
l=8, m=5, 24
l=11, m=7, -27
l=19, m=12, -219
l=27, m=17, 108
l=46, m=29, 281
l=65, m=41, 867
l=84, m=53, -6143
l=149, m=94, 2419
l=233, m=147, 4862
l=317, m=200, 9266
l=401, m=253, 19584
l=485, m=306, 75028
l=569, m=359, -81063
l=1054, m=665, -3664765
l=1539, m=971, 72058
.
.
.
The initial difference between successive (l, m) values is (1, 1).
After the 2l-3m values change signs, the difference between successive (l, m)
values becomes (2, 1) (the (l, m) value immediately before the
sign change). After the 2l-3m values change signs again, the difference between
successive (l, m) values becomes (3, 2) (the (l, m)
value immediately before the sign change), etc. Note that the Ml,m/|2l-3m|
values increase until the sign changes.
Empirical results (showing why the parity vector p is of importance)
are;
(13) If the maximum Ml,m/|2l-3m|,
l=m+k, m=1, 2, 3, ..., value occurs immediately before the sign
change of 2l-3m, then the (l, m)
value is that of an M-cycle generated from the parity vector p.
(14) If the maximum Ml,m/|2l-3m|,
l=m+k, m=1, 2, 3, ..., value occurs at the sign change of 2l-3m
and the (l, m) value is not that of an M-cycle generated
from the parity vector p, then the (l-1, m-1) value is that of an M-cycle
generated from p.
A graph of Ml,m/|2l-3m|,
l=m+k, m=1, 2, 3, ..., 10 and k=1, 2, 3, ..., 10
is;

Let k1 denote the difference between the l and m
values of a generalized continued-fraction convergent of log(3)/log(2) where
l and m are relatively prime. Let k2 denote
the difference between the l and m values of the next generalized
continued-fraction convergent of log(3)/log(2) where gcd(l, m)=1
and denote Ml,m/|2l-3m|
for this (l, m) value by min2. An
empirical result is;
(15) The Ml,m/|2l-3m|
values where k1<l-m<k2 are less than
min2 except possibly when (l, m) is a
generalized continued-fraction convergent of log(3)/log(2) where gcd(l,
m)≠1.
For example, (149, 94) is a generalized continued-fraction convergent of
log(3)/log(2) where gcd(l, m)=1 and in this case k1=55
and Ml,m/|2l-3m|=2419.
For the next generalized continued-fraction convergent of log(3)/log(2) where
gcd(l, m)=1 ((233, 147)), k2=86, and Ml,m/|2l-3m|=4862.
For k=55, 56, 57, ..., 86, the largest Ml,m/|2l-3m|
values occur for (l, m)=(149, 94), (152, 96), (154, 97), (157,
99), (160, 101), (163, 103), (165, 104), (168, 106), (171, 108), (173, 109),
(176, 111), (179, 113), (182, 115), (184, 116), (187, 118), (190, 120), (192,
121), (195, 123), (198, 125), (201, 127), (203, 128), (206, 130), (209, 132),
(211, 133), (214, 135), (217, 137), (219, 138), (222, 140), (225, 142), (228,
144), (230, 145), and (233, 147) respectively and the Ml,m/|2l-3m|
values (truncated) are 2419, 219, 130, 388, 433, 142, 220, 6143, 219, 158, 558,
390, 147, 281, 1605, 219, 191, 867, 361, 152, 356, 1004, 219, 231, 1561, 340,
175, 463, 763, 219, 281, and 4862 respectively. The only Ml,m/|2l-3m|
value larger than 4862 (6143) occurs when (l, m)=(168, 106), a
generalized continued-fraction convergent of log(3)/log(2) where gcd(l,
m)≠1.
Upper bounds of minima in 3n+c cycles can then be determined using the
generalized continued-fraction convergents of log(3)/log(2).
Miscellaneous Properties of Minima in 3n+c Cycles
When the element following an odd element i in the 3n+c
sequence is defined to be (3i+c)/2 instead of 3i+c,
1-2 sequence vectors become 0-1 sequence vectors. Note that 2m must
be greater than l for there to be any cycles having 0-1 sequence vectors.
For example, when l=11 and m=7, the parity vectors of cycles
having 0-1 sequence vectors are (1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1), (1, 1, 0, 1,
1, 0, 1, 0, 1, 1, 0), (1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1), (1, 0, 1, 1, 0, 1, 0, 1,
0, 1, 1), and (1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1) (corresponding to primitive
cycles for c=139). The 3n+139 cycle corresponding to the
second parity vector is {-4151, -6157, -9166, -4583, -6805, -10138, -5069,
-7534, -3767, -5581, -8302} and twice the largest element in the cycle (-3767)
is greater than the smallest odd element (-6805). In the other
interrelated 3n+139 cycles having 0-1 sequence vectors, twice the largest element in a cycle is not greater than the
smallest odd element in the cycle. Let min denote the element of a
cycle in the 3n+c sequence having the smallest absolute value and
let max denote the odd element having the largest absolute value.
More
empirical results are;
(16) If c=|2l-3m| and 2m>l,
there is at least one primitive cycle having a 0-1 sequence vector and there are
usually primitive cycles not having 0-1 sequence vectors. If
c=|2l-3m|, 2m>l,
and
the greatest common divisor of l and m is 1, there is at least one
cycle among the interrelated primitive cycles having 0-1 sequence vectors where 2|min|>|max|
(there is no cycle among the interrelated primitive cycles not having 0-1 sequence
vectors where 2|min|>|max|).
If c=|2l-3m|, 2m<l, and
gcd(l, m)=1, there is at least one cycle among the
interrelated primitive cycles where 2|min|>|max|.
(17) 2|min|>|max| for a primitive 3n+c cycle where gcd(l, m)=1
only if c=|2l-3m|.
Usually, if c=|2l-3m|, 2m>l,
and gcd(l, m)=1, there is exactly one cycle among
the interrelated primitive cycles having 0-1 sequence vectors where 2|min|>|max|.
When c=1675, l=9, and m=7, there are two primitive cycles
where 2|min|>|max|. For one of these cycles, min=-2219,
max=-4429, and 2|min| is barely greater than |max| (min=-2363
and max=-3997 for the other cycle). Usually, if c=|2l-3m|,
2m>l, and gcd(l, m)≠1,
there is at least one cycle among the interrelated primitive cycles having 0-1
sequence vectors where 2|min|>|max|. When c=9823,
l=14, and m=8, there doesn't appear to be a primitive cycle where 2|min|>|max|.
If c=|2l-3m|, 2m<l, and
gcd(l, m)=1, there appears to be exactly one cycle among the
interrelated primitive cycles where 2|min|>|max|. If c=|2l-3m|,
2m<l, and gcd(l, m)≠1, there doesn't appear
to be a primitive cycle where 2|min|>|max|. Usually, if a
primitive 3n+c cycle where c properly divides 2l-3m
exists and gcd(l, m)≠1, then 2|min| is not greater
than |max|. When c=145, l=12, and m=8, min=-617,
max=-1231, and 2|min| is barely greater than |max|.
Also, when c=493, l=12, and m=8, min=-1829, max=-3635,
and 2|min| is barely greater than |max|.
A graph of the proportions of 3n+c cycles having 0-1 sequence vectors for
c less than or equal to 499, 997, 1499, 1999, ..., 9997 is;
More on m-Cycles
Let K denote the number of odd elements in a 3n+1 cycle (n>0)
and L the number of even elements.
In 2004, Simons8 proved that if a nontrivial 2-cycle exists, then (K+L,
K) must be a convergent in the continued-fraction expansion of log2
3. Let δ denote log(3)/log(2). Using an empirically derived lower bound for the minimum element in an m-cycle,
Simons and de Weger9 proved that δK<K+L<1.000001δK.
As shown above, 3n+c cycles with large elements and having a
constrained dynamic range behave similarly, that is, the (K+L,
K)
values include the generalized continued-fraction convergents of log(3)/log(2).
This will be discussed in more detail in following sections.
Characterization of Cycles in the 3n+c Sequence
Attachment points in a cycle are defined to be even integers i such
that i-c is divisible by 3 (and (i-c)/3 is not already in the
cycle). An attachment point i will be said to be primary if 4i
is not an attachment point. If i is a primary attachment point and
4 divides i, then i/4 will be said to be the secondary attachment
point, etc. In the cycle for c=1, -68 is the only attachment point.
(There are no attachment points in the other known 3n+1 cycles.) In
the following, 3n+c sequences are extended backwards from attachment
points. "Odd" paths are taken, that is, if i is an even integer in
the extended sequence and 3 divides i-c, then the path (i-c)/3
(and not 2i) is taken. Presumably, an odd integer divisible by 3
(denoted by t) will be reached. The t value of a primary
attachment point will be said to be the "proxy" of
the first odd element in the cycle after the preceding primary attachment point
(in the case where there is only one primary attachment point, the preceding
primary attachment point is the primary attachment point). (Note that the
sequence vector of the cycle elements starting with the first odd element after
the preceding primary attachment point and ending with the primary attachment
point is a 0-1 sequence vector; this is the motivation for taking "odd" paths
when extending sequences backwards from attachment points. For the c=1 cycle, t
equals -21 and is the proxy of the cycle element -17.) As will be shown, the
proxy concept allows a simplified description of 3n+c cycles
with attachment points. The extended sequences have many properties and, unlike
Bohm and Sontacchi's formula, are amenable to Diophantine analysis. Cycles with
at least one attachment point will be considered in this section and the next
seventeen sections (cycles with no attachment points will be discussed at the end of the article).
An empirical result is;
(18) There exists at least one primitive 3n+c cycle having an
attachment point for every c value.
Let u denote the first odd element in a 3n+c cycle after a
primary attachment point. In this article, the average of the |u|
values and the absolute values of their proxies is used to characterize a 3n+c
cycle. Let a denote the number of primary attachment points in a cycle.
When a>0, the average of the |u| values and the absolute values
of their proxies will be taken to be the maximum
likelihood estimator for the parameter λ of an exponential probability
distribution (f(x; λ)=λe-λx, x≥0).
The function g(x)=λe-λx where positive and
negative x values are allowed will be used to compute the domain of the
absolute values of the u values and the absolute values of their proxies. The domain of the
absolute values of the u values and the absolute values of their proxies is determined by
-log(|u1|/λ)/λ, -log(|t1|/λ)/λ,
-log(|u2|/λ)/λ, -log(|t2|/λ)/λ, -log(|u3|/λ)/λ, -log(|t3|/λ)/λ, ...,
-log(|ua|/λ)/λ, -log(|ta|/λ)/λ.
For example, the (u, t) values for a cycle for c=121 are
(19, -9), (395, 51), (65, 39), (119, 183), (335, 147), (281, 27), (101, -237),
(53, -63), (35, 21), and (23, -159). A plot of the |u| and |t| values versus their domain
is;

(The x values have been scaled up by a factor of 104
and all but two data points are shown. No shape-preserving interpolation
of the data points is done.) Note that all the u
and t values in a cycle are distinct (although two t values can
have the same absolute value). The domain of the absolute values of the
u values and the absolute values of their proxies appears to
be a small interval about zero, the largest x value usually being larger
than the absolute value of the smallest x value (so that the maximum |u|
or |t| value times the minimum |u| or |t| value is usually
less than λ2). Let utmax denote the
maximum |u| or |t| value in a cycle and utmin
the minimum |u| or |t| value. An empirical result (based on the
663743 cycles for the c
values less than or equal to 199999) is;
(19) utmaxutmin/λ2 is
almost always less than δ.
A histogram of the utmaxutmin/λ2
values for the cycles where c≤199999 is;

Fifty bins are used.
A histogram of the 65 values greater than δ is;

Ten bins are used. The maximum value is 2.1673 (less than δ2).
The a values of these cycles are small (less than or equal to 28) and the
|L-K| values are relatively small. In fourteen of
these cycles, L=K. Also, 2K≥L if L>K and 2L>K
if L<K. The rationale for
including the absolute values of the proxies in the average is that they appear
to have the same exponential curve as the |u| values. Of course, |u|
values are local minima and their average is related to the minimum in a
cycle.
Belaga10 proved that if 2l-3k>0
where l is the length of and k is the number of odd elements in a
3x+d cycle (x>0), then 1 ≤ n < d/(2l/k-3)
where n is the smallest odd element in the cycle. Let umax
denote the largest |u| value in a cycle and umin the
smallest |u| value. Let tmax denote the largest |t|
value in a cycle and tmin the smallest |t| value.
Empirical results (based on the cycles where c≤199999) are;
(20) If L<K, 2c/utmin>|2(K+L)/K-3|.
If L≥K, c/utmin>|2(K+L)/K-3|.
If L<K, 3c/umin>|2(K+L)/K-3|.
If L≥K, c/umin>|2(K+L)/K-3|.
(21) |1-c/utmin|, |1-c/umin|,
and |1-c/tmin| are usually greater than |2(K+L)/K-3|.
A histogram of the a values
for the 4458 exceptions for utmin
is;

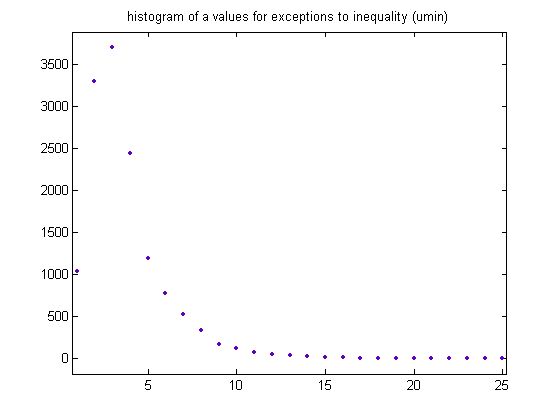
The largest a value is 15. A histogram of the
a values for the 13811 exceptions for umin
is;
The largest a value is 30. A histogram of the
a values for the 13698 exceptions for tmin
is;

The largest a value is 17. The respective
percentages of exceptions for utmin,
umin, and tmin
are 0.67%, 2.08%, and 2.06%. The expressions "1+c/X0"
and "|1-c/X0|"
where X0 is a lower bound of the minimum in an m-cycle are relevant to Simons and de Weger's work. An empirical result (based on the
27041 cycles having the (K+L, K) value of
an M-cycle generated from the parity vector p for
c less than or equal to 199999) is;
(22) If the (K+L, K) value of a cycle equals that
of an M-cycle generated from the parity vector p, |1-c/utmin|
and |1-c/tmin| are almost always greater than |2(K+L)/K-3|.
If the (K+L, K) value of a cycle equals that of an M-cycle
generated from the parity vector p, |1-c/umin| is
greater than |2(K+L)/K-3|.
The (c, L, K, a) values for the exceptions (for
utmin and tmin) are (1631, 5, 8, 2), (36791,
15, 25, 3), (36791, 15, 25, 4), and (186793, 9, 15, 2).
Empirical results (based on the cycles having the (K+L, K)
value of an M-cycle generated from the parity vector p for c
less than or equal to 199999) are;
(23)
If the (K+L, K) value of a cycle equals that of an M-cycle generated from the
parity vector p, utmax is greater than cNK+L,K/|2K+L-3K|/6
and utmin is less than cMK+L,K/|2K+L-3K|.
(24) If the (K+L, K) value of a cycle equals that of an M-cycle
generated from the parity vector p, δ2a+14>utmax/utmin.
(The latter proposition may fail for very large upper bounds of c
values.)
Let i denote the smallest power of δ such that δi>utmax/utmin.
A histogram of the i-2a values of the cycles having (K+L,
K) values equal to those of M-cycles generated from the parity
vector p for c less than or equal to 997 is;

This distribution has a mean, standard deviation, and sample size of -1.1163,
2.3629, and 301 respectively. A histogram of the i-2a values of the cycles having (K+L,
K) values equal to those of M-cycles generated from the parity
vector p for c=7153 is;

This distribution has a mean, standard deviation, and sample size of
-0.6905, 1.3898, and 2843 respectively. A histogram of the i-2a values of the cycles having (K+L,
K) values equal to those of M-cycles generated from the parity
vector p for c less than or equal to 49999 is;

This distribution has a mean, standard deviation, and sample size of -1.3532,
2.4842, and 9332 respectively.
A histogram of the i-2a values of the cycles having (K+L,
K) values equal to those of M-cycles generated from the parity
vector p for c less than or equal to 99997 is;

This distribution has a mean, standard deviation, and sample size of
-1.4960, 2.6018, and 14663 respectively. For c upper bounds of
19999, 39997, 59999, 79999, 99997, 119999, 139999, 159997, 179999, and 199999,
the distributions have respective means of -1.1470, -1.3009, -1.3818, -1.4450,
-1.4960, -1.5158, -1.4805, -1.5319, -1.6246, and -1.4388, respective standard
deviations of 2.3157, 2.4634, 2.5125, 2.5437, 2.6018, 2.6466, 2.6293, 2.6861,
2.7751, and 2.5766, and respective sample sizes of 5811, 7604, 9629, 14365,
14663, 14704, 15672, 15919, 16443, and 27041. The standard deviation
generally increases as the c upper bound increases, but in an irregular
fashion. When c=185357, the distribution has a mean, standard
deviation, and sample size of -1.4773, 2.3212, and 6321 respectively. When
c=186793, the distribution has a mean, standard deviation, and sample size
of -0.5107, 1.5784, and 4161 respectively. For a c value having a
large sample size, the standard deviation of the distribution is generally
smaller than that of the composite distribution.
Let i denote the smallest power of δ such that δi>utmax/utmin.
A table of the number of i values for given a values of the 3n+c
cycles for c less than or equal to 99997 is; a=1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
i=1 3423 253 5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
2 1845 1858 182 29 8 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
3 1003 4035 1254 254 45 8 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
4 428 3412 2103 791 213 59 28 4 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
5 267 2542 3113 1688 689 256 101 29 13 6 0 1 0 0 0 0 0 0 0 0 0 0 0 0
6 145 1829 3082 2322 1389 707 332 153 74 44 22 10 5 2 1 0 0 0 0 0 0 0 0 0
7 103 1245 2546 2579 1919 1242 726 452 294 161 86 70 37 13 10 5 6 4 1 0 0 0 0 0
8 66 886 2149 2488 2066 1539 1183 851 592 363 306 166 125 76 47 39 24 14 13 8 7 3 4 2
9 45 602 1590 2012 1968 1770 1461 1089 913 703 516 410 252 212 161 132 99 80 49 35 34 18 12 13
10 25 397 1161 1592 1662 1625 1526 1335 1051 914 775 590 482 389 332 257 210 173 146 118 81 88 80 61
11 31 297 726 1116 1340 1345 1310 1250 1206 1048 893 735 641 543 485 393 331 311 267 217 215 156 134 121
12 13 193 483 782 943 1081 1140 1117 1041 923 932 755 704 634 551 518 494 423 411 283 308 294 257 220
13 11 139 326 505 661 750 869 856 866 815 802 727 696 609 603 534 552 521 442 455 379 381 321 287
14 8 96 193 324 448 596 616 700 697 696 664 626 609 602 552 547 523 494 501 397 402 423 355 363
15 6 49 135 222 318 368 462 501 506 503 519 474 473 491 489 524 485 479 413 412 435 409 334 369
16 7 43 78 127 197 261 320 343 363 372 419 397 410 411 388 417 417 386 400 362 370 355 349 305
17 4 18 67 95 123 151 205 229 232 283 260 264 276 322 309 313 318 316 312 290 315 309 298 255
18 3 10 34 58 66 117 136 164 178 185 200 216 214 217 216 227 264 257 260 261 229 234 234 259
19 1 6 17 36 59 62 82 90 124 141 131 134 153 138 155 158 169 172 178 208 193 185 185 167
20 2 8 15 23 34 54 54 92 65 64 88 93 103 115 129 134 138 138 152 160 127 146 131 129
21 1 1 10 22 26 29 38 43 63 49 65 98 76 74 106 96 92 110 111 114 101 110 105 115
22 2 4 5 5 10 26 25 34 42 44 44 58 55 65 64 62 70 65 74 72 75 68 75 70
23 0 2 1 7 14 6 17 19 18 21 33 32 36 29 40 42 41 53 48 56 57 55 51 65
24 0 0 1 5 4 6 8 9 12 18 16 24 21 28 21 30 25 40 26 42 36 38 22 37
25 1 0 0 2 2 3 5 9 8 13 13 17 15 19 20 21 28 25 24 30 20 27 20 25
26 0 0 0 1 1 4 5 2 4 8 11 9 7 11 8 15 12 11 17 21 17 21 22 18
27 0 0 3 0 2 2 4 5 7 6 8 3 9 10 4 9 15 11 18 10 14 15 8 7
28 0 0 0 0 1 0 2 4 4 3 0 3 7 4 5 9 9 7 8 7 4 6 9 16
29 0 0 0 1 2 2 0 1 0 1 1 4 2 5 4 5 5 7 8 6 5 7 2 8
30 0 0 0 0 0 0 1 1 1 2 1 3 1 2 3 3 2 2 3 2 1 3 2 5
31 0 0 0 0 0 0 0 0 1 1 0 1 1 1 0 1 3 4 2 0 0 0 3 0
32 0 0 0 0 0 0 0 0 0 0 0 2 1 0 0 1 0 0 2 3 1 1 0 3
33 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 2 0 0 2 3
34 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 1 0 1 1 0 1 0 0 0
35 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 1
36 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0 2
37 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0
38 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
39 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
For a=1, 2, 3, ..., 24, the means of these distributions are 2.3075,
5.0025, 6.9688, 8.2655, 9.3172, 10.2088, 10.9385, 11.5711, 12.0145, 12.4725,
12.8472, 13.3144, 13.6613, 14.0181, 14.2853, 14.6265, 14.8641, 15.0889, 15.3236,
15.6876, 15.6275, 15.8181, 15.9344, and 16.2146 respectively, the standard deviations are 2.0704, 2.7025,
2.8688, 2.9650, 3.0535, 3.1151, 3.1678, 3.2250, 3.2571, 3.3044, 3.3179,
3.5003, 3.4540, 3.4775, 3.4843, 3.5874, 3.5740, 3.6121, 3.6397, 3.6950, 3.5507,
3.5912, 3.5758, and 3.7751 respectively, and the sample sizes are 7440, 17925, 19279, 17086, 14210,
12069, 10658, 9383, 8375, 7388, 6805, 5922, 5412, 5023, 4704, 4495, 4334, 4105,
3887, 3572, 3428, 3353, 3016, and 2926 respectively. A plot of
the means and standard deviations is;

A linear least-squares fit of the means plotted against log(a) is;

For c less than or equal to 199999 and a=1, 2, 3, ..., 24, the
means of the distributions are 2.3960, 5.0181, 6.9037, 8.2448, 9.3514, 10.2428,
10.9874, 11.5606, 12.0565, 12.4427, 12.8846, 13.3813, 13.7249, 14.0554, 14.2985,
14.5896, 14.8762, 15.0961, 15.3512, 15.6148, 15.6866, 15.8611, 15.9868, and
16.2639 respectively, the
standard deviations are 2.1291, 2.7093, 2.8870, 2.9846, 3.0753, 3.1413, 3.1873,
3.2188, 3.2653, 3.3025, 3.3770, 3.5027, 3.4663, 3.5132, 3.4893, 3.5289, 3.5896,
3.5850, 3.6588, 3.7029, 3.6014, 3.6314, 3.6232, and 3.7260 respectively, and the sample sizes
are 10995, 31363, 38306, 33299, 27300, 23335, 20718, 18800, 16910, 15307, 13815,
12411, 11597, 10821, 10147, 9817, 9199, 8784, 8420, 8048, 7673, 7422, 6682, and
6371 respectively. The means and standard deviations of the
distributions do not change much for different upper bounds of c values.
An empirical result (based on the 663743 cycles with attachment points for c less than or equal
to 199999) is;
(25) δa+1>utmax/λ.
Let i denote the smallest power of δ such that δi>utmax/λ.
A table of the number of i values for given a values of the 3n+c cycles for c less than or
equal to 99997 is; a=1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
i=1 6226 4689 984 224 43 11 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
2 1214 10462 9699 5654 2684 1338 697 332 154 92 49 21 10 12 1 2 1 0 0 0 0 0 0 0
3 0 2774 7635 9026 8045 6440 5074 3883 2929 2135 1716 1270 913 701 571 466 366 316 224 169 142 115 101 73
4 0 0 961 2121 3161 3788 4081 4052 3908 3562 3303 2779 2494 2237 2015 1784 1730 1471 1353 1132 1067 1001 822 782
5 0 0 0 61 277 487 774 1043 1249 1428 1495 1530 1583 1572 1555 1555 1487 1517 1457 1373 1265 1278 1161 1135
6 0 0 0 0 0 5 30 73 134 169 235 298 383 462 499 607 644 664 704 727 742 762 710 686
7 0 0 0 0 0 0 0 0 1 2 7 24 29 38 62 79 102 129 139 157 198 187 205 227
8 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 2 4 8 10 14 14 10 16 21
9 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2
The means and standard deviations of these distributions for a=1, 2,
3, ..., and 24 are 1.1632, 1.8932, 2.4447, 2.7741, 3.0665, 3.2831, 3.4708,
3.6421, 3.7950, 3.9260, 4.0253, 4.1496, 4.2777, 4.3761, 4.4613, 5.5660, 4.6297,
4.7181, 4.7970, 4.8917, 4.9501, 4.9806, 5.0491, and 5.0967 respectively and 0.3695, 0.6364, 0.6699, 0.6861, 0.7050, 0.7165,
0.7371,
0.7547, 0.7717, 0.7878, 0.8047, 0.8381, 0.8502, 0.8718, 0.8869, 0.9147, 0.9237,
0.9445, 0.9407, 0.9536, 0.9793, 0.9554, 0.9822, and 0.9891 respectively. A plot of these values is;

The means and standard deviations of these distributions (and
the distributions themselves) do not change much for different upper
bounds of c values. A linear least-squares fit of the means
plotted against log(a) is;

For c less than or equal to 199999 and a=1, 2, 3, ..., 24, the
means of the distributions are 1.1843, 1.9007, 2.4258, 2.7702, 3.0672, 3.2924,
3.4819, 3.6423, 3.8029, 3.9201, 4.0369, 4.1636, 4.2806, 4.3784, 4.4652, 4.5543,
4.6415, 4.7115, 4.7964, 4.8831, 4.9571, 4.9980, 5.0503, and 5.1163 respectively
and the standard deviations are 0.3877, 0.6345, 0.6626, 0.6896, 0.7049, 0.7218,
0.7356, 0.7564, 0.7710, 0.7909, 0.8143, 0.8350, 0.8608, 0.8690, 0.8859, 0.9013,
0.9226, 0.9423, 0.9380, 0.9441, 0.9708, 0.9649, 0.9948, and 0.9876 respectively.
The Chain Equation
The chain equation for an m-cycle is given
by 3k(i)ai-1=2k(i+1)+l(i)ai+1-2l(i),
i=0, 1, 2, ..., m-1, where k(i) is the number of
successive odd numbers leading up to a local maximum (due to typographical
difficulties, k(i) is used to denote ki), l(i)
is the number of successive even numbers going down to the next local
minimum (due to typographical difficulties, l(i) is used to denote li),
and ai are natural numbers (see Simons and de Weger's
article).
The chain equation is the starting point of m-cycle theory and is
used to derive Simons and de Weger's Lemma 4;
0 < Λ < ∑1/xi
where xi is a local minimum, the summation is from
i=1 to m, and Λ denotes (K+L) log(2)-K
log(3).
The above characterization of a 3n+c cycle is related to this
lemma. For most 3n+c cycles, c times the sum of the reciprocals of
|u| and |t| is greater than the absolute value of Λ. When (K+L,
K) is equal to (or approximately equal to) a generalized continued-fraction
convergent of log(3)/log(2), c times the sum of reciprocals is sometimes smaller
than the absolute value of Λ. An empirical result (based on the
cycles with attachment points for c≤199999)
is;
(26) 10c∑(1/|ui| + 1/|ti|)
where the summation is from i=1 to a is greater than
|Λ|. 16c∑1/|ui|
where the summation is from i=1 to a is greater than
|Λ|. 128c∑1/|ti|
where the summation is from i=1 to a is greater than
|Λ|.
Simons and de Weger's Corollary 5 (of Lemma 4) is;
0 < Λ < m/xmin
≤ m/X0
where xmin is the global minimum of an m-cycle
and X0 is an empirically derived lower bound for xmin.
(As will be shown, the chain equation is not entirely applicable to the above
characterization of a 3n+c cycle, so even if Proposition (26) is
accepted, a proposition analogous to Corollary 5 can't be derived without some
knowledge of the relative sizes of the |u| and |t| values.)
Simons and de Weger show that Λ is exponentially small in terms of its
coefficients and use a result from transcendence theory due to Rhin11
to derive Lemma 12;
Λ > e-13.3(0.46057+log
K).
Using Corollary 5 gives Simons and de Weger's Corollary 13 (where the global minimum of an m-cycle is estimated
in terms of K);
xmin <
me13.3(0.46057+log K)
Brox12 proved that for any m there are only finitely many
m-cycles.
The Number of M-Cycles
A histogram of the [3·log(c)]-a
values
for the 27014 cycles for c less than or equal to 199999 having (K+L,
K) values equal to those of M-cycles generated by the parity
vector p is;

This distribution has a mean of 29.2260 and a standard deviation of 4.3270.
The only negative value (-1) occurs for the c=1 cycle. Also, small
values only occur for small c values. Denote the (L,
K) value of a cycle generated from the parity vector p by (L',
K'). If the (L, K) value of a cycle doesn't equal that
of an M-cycle generated from the parity vector p, but K=K'
for some K', set d to |L-L'|, otherwise set d
to zero. If K≠K' for any K' then K+1=K'
for some K', and if K≠1,
K-1=K'
for some K'. In this case, set d to the absolute
value of L minus the average of the corresponding L' values. If K=1, set d to
|L-L'| where K+1=K'. An empirical
result (based on the 663743 cycles with attachment points for c less than or equal to
199999) is;
(27)
[3·log(c)+d/δ] is almost
always greater than a.
This proposition is true for 99.9235% of the cycles. (Current m-cycle theory lacks such a relationship between (L,
K) and m.) A histogram of the [3·log(c)+d/δ]-a values for
the 23132 cycles with attachment points for c less than or equal to 9997
superimposed on a normal probability distribution having the same mean and
standard deviation is;

When c=32389, the difference is -14 for a cycle where (L,
K)=(876, 984) and a=234. When c=33989, the difference is -13 for a cycle where (L,
K)=(1116, 1224) and a=296. When c=22429, the difference is -13 for a cycle where (L,
K)=(553, 689) and a=137. When c=45679, the difference is
-12 for a cycle where (L, K)=(527, 646) and a=138.
When c=43925, the difference is -10 for a cycle where (L, K)=(680,
800) and a=175. When c=45613, the difference is -10 for a
cycle where (L, K)=(1181, 1345) and a=290. When c=21809, the difference is
-9 for a cycle where (L, K)=(480, 576) and a=129.
When c=6515, the difference is -8 for a cycle where (L, K)=(436,
506) and a=122. When c=11707, the difference is -7 for a cycle where (L, K)=(624,
713) and a=165. When c=43739, the difference is -7 for a
cycle where (L, K)=(969, 1083) and a=250. When c=46823,
the difference is -7 for a cycle where (L, K)=(1105, 1192) and
a=296. When c=5827, the difference is -6 for a cycle where (L, K)=(426,
504) and a=114. When c=27547,
the difference is -5 for a cycle where (L, K)=(588, 696) and a=149.
When c=39605, the difference is -5 for a cycle where (L, K)=(912,
1016) and a=237. When c=28771, the difference is -5 for a cycle where (L, K)=(738,
843) and a=190. When c=42641, the difference is -5 for a
cycle where (L, K)=(1555, 1722) and a=382.
When c=46841, the difference is -5 for a cycle where (L, K)=(585,
690) and a=151. When c=48091, the difference is -5 for a
cycle where (L, K)=(596, 720) and a=147. When c=35191, the difference is -4 for a
cycle where (L, K)=(522, 672) and a=135. When c=8243, the difference is -4 for a
cycle where (L, K)=(805, 929) and a=196. When c=16001, the difference is -4 for a
cycle where (L, K)=(613, 726) and a=151. When c=14957,
the difference is -3 for a cycle where (L, K)=(500, 591) and a=129.
When c=16487, the difference is -3 for a cycle where (L, K)=(529,
625) and a=134. When c=17315, the difference is -3 for a
cycle where (L, K)=(696, 750) and a=194. When c=26213,
the difference is -3 for a cycle where (L, K)=(428, 514) and a=113.
When c=46801, the difference is -3 for a cycle where (L, K)=(564,
664) and a=145. When c=17449, the difference is -2
for a cycle where (L, K)=(336, 454) and a=94. When c=38689, the difference is -2 for a cycle where (L,
K)=(633, 726) and a=164. When c=20807,
the difference is -2 for a cycle where (L, K)=(484, 590) and a=119.
When c=22343, the difference is -2 for a cycle where (L, K)=(1185,
1282) and a=306. When c=41893, the difference is -2 for a
cycle where (L, K)=(471, 549) and a=128. (There
is only one cycle each for c equal to 6515, 14957, 17315, 28771, 32389, 33989,
39605, 42641, and 48091. There are only two cycles each for c equal to
5827, 8243, 11707, 16001, 17449, 20807, 21809, 22429, 27547, 35191, 41893,
43925, 45613, and 45679. The largest number of cycles occurs for c=46841;
there are ten cycles having four distinct (L, K) values.
Except for c=22343, the (L, K) values of all the cycles for
the above c values are large. When c=22343, there are four
cycles having (L, K) values of (1185, 1282), (1080, 1027), (7,
17), and (7, 17).) Also, the difference is -1 for
9 cycles when c
is less than or equal to 49999. Similar results apply for c
greater than 50000. Let cmax denote the upper
bound of the c values. Other than
being discrete-valued, the distribution of differences resembles a normal probability
distribution where the mean is approximately equal to the variance for
relatively small cmax values (the mean of
the above distribution is 24.579 and the standard deviation is 5.061).
Assuming the d/δ-a values cancel each other out, the expected mean
is (1/n)∑(3·log(c)) where n is the number
of c values less than or equal to cmax. The
expected mean of the above distribution is 24.631. A normal
probability plot of the differences for the 102 cycles for the c values less
than
or equal to 97 is;

The mean of this distribution is 9.716 with a 95% confidence interval of
(9.066, 10.365) and the standard deviation is 3.308 with a 95% confidence
interval of (2.907, 3.836). The expected mean is 10.785. When cmax=997,
the mean of the distribution of differences is 16.949 and the standard deviation
is 3.918 (there are 1556 cycles with attachment points for this cmax
value). A plot of the distribution
of differences superimposed on a normal probability distribution having the same
parameters is;

For larger cmax values, a normal probability distribution
doesn't fit the data very well. When cmax=19999, the
mean of the distribution of differences is 26.879 and the standard deviation is
5.957 (there are 48449 cycles with attachment points for this cmax
value). A plot of the distribution of differences superimposed on a normal
probability distribution having the same parameters is;

When
cmax=29999, the mean of the distribution of differences is 28.332
and the standard deviation is 6.612. A plot of the distribution
of differences superimposed on a normal probability distribution having the same
parameters is;

A detailed plot showing the left-hand tails of the above distributions is;

A plot of the means, standard deviations,
and expected means of the distributions of differences versus log(cmax) for cmax values of 997, 1999, 2999, 3997,
4999, 5999, 6997, ..., 49999 is;

(The curves for the means and expected means intersect.) Although the
mean starts out being smaller than the expected mean and eventually becomes
larger than the expected mean, the curve of means still appears to be mostly linear
(when plotted against log(cmax)).
A quadratic (f(x)=p1x2+p2x+p3) least-squares fit of the means plotted against log(cmax)
for cmax=997, 1999, 2999, ..., 199999 is;

p1=0.1109 with a 95% confidence interval of (0.1067, 0.1151),
p2=1.346 with a 95% confidence interval of (1.258, 1.434), and
p3=2.688 with a 95% confidence interval of (2.23, 3.147).
SSE=0.3537, R-square=0.9999, adjusted R-square=0.9999, and RMSE=0.04237.
The non-linearity
of the standard deviation curve is due to a large number of cycles with
attachment points (2849) for c=7153. A cubic (f(x)=p1x3+p2x2+p3x+p4)
least-squares fit of the standard deviations plotted against log(cmax)
for cmax=997, 1999, 2999, ..., 199999 is;

p1=0.02579 with a 95% confidence interval of (0.0208, 0.03079),
p2=-0.5298 with a 95% confidence interval of (-0.6803,
-0.3792), p3=4.046 with a 95% confidence interval of (2.55,
5.542), and p4=-7.176 with a 95% confidence interval of
(-12.07, -2.28). SSE=1.053, R-square=0.9976, adjusted R-square=0.9976, and
RMSE=0.07328. When c=40741, there are 1429 cycles with attachment points. The
total number of cycles is large enough for cmax=40999 that
there is only a minor drop in the standard deviation due to these cycles.
There are also 3782 cycles with attachment points for c=71515, 1238
cycles with attachment points for c=72023, and 1658 cycles with
attachment points for c=84095 (and larger numbers of cycles for larger
c values).
The expected number
of cycles is cmax/log(cmax) times the
expected mean. A plot of the expected number of cycles and the number of
cycles having attachment points for cmax values of 997, 1999, 2999, ..., 49999 is ;

For these cmax values, the expected number of cycles is larger than the actual number of cycles.
The expected number of cycles becomes smaller than the actual number of cycles for larger cmax
values.
A quadratic least-squares fit of the number of cycles plotted against (cmax+1)/1000
or (cmax+3)/1000 (when 1000 does not divide cmax+1)
for cmax=997, 1999, 2999, ..., 199999 is;

(The coefficients are poorly conditioned when the number of cycles is plotted
against cmax.) p1=3.081 with a 95%
confidence interval of (2.951, 3.211), p2=2750 with a 95%
confidence interval of (2723, 2777), and p3=-8472 with a 95%
confidence interval of (-9645, -7299). SSE=1.517e+09, R-square=0.9998, adjusted
R-square=0.9998, and RMSE=2775.
A linear least-squares fit of the proportions of
cycles in the left-hand tail of the distribution of differences (up to and including cycles for
which the difference is 0) plotted against (cmax+1)/1000 or (cmax+3)/1000
for cmax=19999, 39997, 59999, ..., 199999 is;

p1=5.014e-5 with a 95% confidence interval of (4.652e-5,
5.376e-5) and p2=0.000286 with a 95% confidence interval of
(0.0002635, 0.0003084). SSE=1.627e-9, R-square=0.9922, adjusted
R-square=0.9912, and RMSE=1.426e-5. Why these proportions appear to be
increasing linearly is unknown.
Modifying the scaling factor (1/δ) slightly has
a significant effect on the distribution of differences. A plot of [3·log(c)+d/1.5]-a
superimposed on a normal probability distribution having the
same parameters for cmax=29999 is;

Even this small of a change in the scaling factor (from 1/1.584962501 to 1/1.5)
skews the distribution significantly (there are fewer negative differences and
more large positive differences). When c=6515, (L, K)=(436,
506), and a=122, the difference is -3 for a cycle. When c=21809,
(L, K)=(480, 576), and a=129, the difference is -4 for a
cycle. When c=22429, (L, K)=(553, 689), and a=137,
the difference is -7 for a cycle. Also, the
difference is -1 for two cycles when cmax=39997. A plot of the means, standard
deviations, and expected means of the distributions of differences versus log(cmax)
for cmax values of 997, 1999, 2999, ..., 29999 is;

The mean of the distribution of differences still appears to increase linearly
(mostly) with log(cmax). A linear least-squares fit of
the means plotted against log(cmax) for cmax=997,
1999, 2999, ..., 29999 is;

A linear least-squares fit of the means plotted against log(cmax)
for cmax=997, 1999, 2999, ..., 29999 when the scaling factor of 1/δ is used is;

A plot of [3·log(c)+d/1.67]-a superimposed on a normal
probability distribution having the same parameters for cmax=29999
is;

A linear least-square fit of the means plotted against log(cmax)
for cmax=997, 1999, 2999, ..., 29999 is;

The slight deviation in the linearity of the means when plotted against log(cmax) is due to the large number of
cycles for c=7153.
A plot of [3·log(c)+d/1.75]-a superimposed on a normal
probability distribution having the same parameters for cmax=9997
is;

For this scaling factor, the distribution is skewed to the left. The
"best" scaling factor is then somewhere between 1/1.75 and 1/1.5. The best
least-squares fit of the means plotted against log(cmax)
appears to occur for the scaling factor of 1/δ.
The [3·log(cmax)]-[3·log(c)]+a
values have a probability distribution resembling that of a chi-square
distribution with 6 degrees of freedom. A histogram of the [3·log(cmax)]-[3·log(c)]+a
values and a plot of the expected numbers of values for a chi-square
distribution for cmax=997 is;

For larger cmax values, a chi-square probability distribution
doesn't fit the data very well. A cubic (f(x)=p1x3+p2x2+p3x+p4)
least-squares fit of the means of the [3·log(cmax)]-[3·log(c)]+a
distributions plotted against log(cmax) for cmax=997,
1999, 2999, ..., and 199999 is;

p1=0.3299 with a 95% confidence interval of (0.2874, 0.3584),
p2=-7.309 with a 95% confidence interval of (-8.379, -6.239),
p3=58.28 with a 95% confidence interval of (47.64, 68.91), and
p4=-152.6 with a 95% confidence interval of (-187.4, -117.8).
SSE=53.2, R-square=0.9982, adjusted R-square=0.9982, and RMSE=0.521. Much of the non-linearity of the curve is due to the large number of cycles with
attachment points for c=7153 (and for a few other c values). A
quadratic (f(x)=p1x2+p2x+p3) least-squares fit
of the corresponding variances of the distributions plotted against
(cmax+1)/1000 or (cmax+3)/1000 (when cmax+1
is not divisible by 1000) is;

(The coefficients are poorly conditioned when the variances are plotted against
cmax.)
p1=0.02988
with a 95% confidence interval of (0.02814, 0.03163), p2=39.04
with a 95% confidence interval of (38.68, 39.41), and p3=-44.09
with a 95% confidence interval of (-59.83, -28.36). SSE=2.732e+05,
R-square=0.9998, adjusted R-square=0.9998, and RMSE=37.24.
For a fixed c value, the
[3·log(c)]-a values may be distributed over several (L,
K) values. For a cycle having the (K+L, K) value of an M-cycle
generated from the parity vector p, 3·log(c)+1≥a. For every c value, there should be only finitely many cycles having
these (K+L,
K) values.
More on the Characterization of 3n+c Cycles
Let λu denote the average of the |u| values
for a cycle and λt the average of the |t| values.
A plot of the |u| values versus their domain for a cycle for c=85
is;

(The x values have been scaled up by a factor of 103 and
all but one data point is shown. No shape-preserving interpolation of the
data points is done. λu equals 368.0.) A plot of
the |t| values versus their domain for the same cycle is;

(The x values have been scaled up by a factor of 103 and
all but one data point is shown. No shape-preserving interpolation of the
data points is done. λt equals 324.0.) An empirical result (based on the
663743
cycles for c less than or equal to 199999) is;
(28) umaxumin/λu2
is almost always less than δ
and tmaxtmin/λt2
is almost always less than δ.
A histogram of the 83 exceptions for u is;

Ten bins are used. The maximum value is 2.1759 (less than δ2).
The a values of these cycles are small (less than or equal to 77) and the
|L-K| values are relatively small. A histogram of the L-K
values is;

The |L-K|/L values are less than 3/8. A histogram of the
51 exceptions for t is;

Ten bins are used. The maximum value is 2.7221 (greater than δ2).
The a values of these cycles are small (less than or equal to 59)
and the |L-K| values are relatively small. A histogram of the
L-K values is;

An empirical result (based on the cycles for c≤199999) is;
(29) δ (a+2)/2>umax/λu
and δ(a+2)/2>tmax/λt.
Let i denote the smallest power of δ such that δi>umax/λu.
A table of i values versus a values for the cycles for c
less than or equal to 9997 is;
a=2
3 4
5 6
7 8
9 10
i=1 2979
912 284
101 31
7 6
2 0
2
870 1315 1048
671 445 302
167 104 93
3
0 139
362 468 439
413 337 304
296
4
0 0
0 35
100 157 161
176 172
5
0 0
0 0
0 2
16 19
46
The means and standard deviations of these distributions for a=2, 3,
4, ..., and 10 are 1.2260, 1.6733, 2.0460, 2.3427, 2.5990, 2.8241, 3.0204,
3.1752, and 3.2817 respectively and 0.4183, 0.5810, 0.6160, 0.6625, 0.7063,
0.7290, 0.7785, 0.7562, and 0.8133 respectively. A plot of these
values is;

A least-squares fit of the means plotted against log(a) is;

Let i denote the smallest power of δ such that δi>tmax/λt.
A table of i values versus a values for the cycles for c
less than or equal to 9997 is;
a=2 3 4 5 6
7 8 9 10
i=1 2857 803 261 75
31 19 4 4 1
2 992 1331 962 613 376
240 151 83 78
3 0 232 471 535 495 462
354 309 294
4 0 0 0 52 113 160
164 190 196
5 0 0 0 0 0
0 14 19 38
The means and standard deviations of these distributions for a=2, 3,
4, ..., and 10 are 1.2578, 1.7587, 2.1240, 2.4424, 2.6798, 2.8661, 3.0480,
3.2264, and 3.3163 respectively and 0.4374, 0.6159, 0.6457, 0.6680, 0.7085,
0.7232, 0.7496, 0.7436, and 0.7806 respectively. A plot of these values
is;

A least-squares fit of the means plotted against log(a) is;

An advantage to working with the average of the |u| and |t|
values (that is, λ) is that the |u| and |t| values are more
evenly distributed along the exponential curve (also, there are distinct maximum and
minimum |u| or |t| values when a=1). Let λ1
denote the average of the |u| and |t| values less than or equal to λ.
If λ1≠utmin, let λ2 denote the average of the |u| and |t|
values less than or equal to λ1, if λ2≠utmin, let λ3 denote
the average of the |u| and |t| values less than or equal to λ2,
etc. An empirical result is;
(30) δa+1 is
usually
greater than λ/λ1, λ1/λ2
(when λ2 is defined), λ2/λ3 (when λ2 and λ3
are defined), etc.
When c is less than or equal to 9997, the proportions of λ/λ1,
λ1/λ2, λ2/λ3, ..., λ5/λ6
values greater than δa+1 are 0.02892 (669/23132),
0.02224 (453/20369), 0.01443 (241/16700), 0.00528 (67/12678), 0.00065 (6/9164),
and 0.00000 (0/6051) respectively.
When c is less than or equal to 19999, the proportions of λ/λ1,
λ1/λ2, λ2/λ3, ..., λ5/λ6
values greater than δa+1 are 0.02334 (1131/48449),
0.01827 (818/44776), 0.01219 (475/38967), 0.00423 (133/ 31452), 0.00063
(15/23967), and 0.00006 (1/16878) respectively.
When c is less than or equal to 29999, the proportions of λ/λ1,
λ1/λ2, λ2/λ3, ..., λ5/λ6
values greater than δa+1 are 0.01920 (1411/73486),
0.01616 (1122/69438), 0.01105 (691/62531), 0.00391 (204/ 52145), 0.00066
(27/40996), and 0.00007 (2/29809) respectively. When a≥3, λ2
and λ3 are usually defined. This is the basis of the following
empirical result;
(31) δ4a+4 is usually greater than utmax/utmin.
If a>3, δ4a+5>utmax/utmin.
Of the 23132 cycles for c less than or equal to 9997, a=1 for 2562
cycles and δ4a+4<utmax/utmin
for 46 cycles (about 1.80% of the cycles), a=2 for 3849 cycles and δ4a+4<utmax/utmin
for 56 cycles (about 1.45% of the cycles), a=3 for 2366 cycles and δ4a+4<utmax/utmin
for 20 cycles, and a≥4 for 14355 cycles and δ4a+4<utmax/utmin
for 4 cycles (in every instance, a=4).
If a=1, δ20>utmax/utmin.
If a=2, δ20>utmax/utmin.
If a=3, δ22>utmax/utmin.
For very large cmax values, larger multiples of a+1
would be required for Proposition (31) to still be valid.
Let i denote the smallest power of δ such that δi>λ/λ1.
For c≤99997 and a=1, 2, 3, ..., 12 , the means of the
distributions of numbers of i values are 1.7859, 2.1929, 2.3974, 2.5008,
2.6018, 2.6874, 2.7393, 2.8119, 2.8246, 2.8736, 2.8835, and 2.9667 respectively,
the standard deviations are 1.7134, 1.2101, 0.9375, 0.8372, 0.8025, 0.7870,
0.7788, 0.8094, 0.7969, 0.8103, 0.8091, and 0.8625 respectively, and the sample
sizes are 7440, 17925, 19279, 17086, 14210, 12069, 10658, 9383, 8375, 7388, 6805, and
5922 respectively.
A linear least-squares fit of the means plotted against log(a) is;

p1=0.4509 with at 95% confidence interval of (0.4186,
0.4832) and p2=1.854 with a 95% confidence interval of (1.796,
1.913). SSE=0.01321, R-square=0.9898, adjusted R-square=0.9887, and
RMSE=0.03634.
For c≤199999 and a=1, 2, 3, ..., 12, the means of the
distributions are 1.8542, 2.2050, 2.3763, 2.4966, 2.6051, 2.6894, 2.7532,
2.8125, 2.8349, 2.8644, 2.9013, and 2.9741 respectively, the standard deviations
are 1.7636, 1.2116, 0.9308, 0.8453, 0.8076, 0.7930, 0.7929, 0.8023, 0.7961,
0.8096, 0.8341, and 0.8607 respectively, and the sample sizes are 10995, 31363,
38306, 33299, 27300, 23335, 20718, 18800, 16910, 15307, 13815, and 12411
respectively. The means and standard deviations of the distributions do
not change much for different c upper bounds.
For the 48449 cycles for c less than or equal to 19999, there are 3374, 5899,
4419, 3297, 2567, and 2073 cycles where a equals 1, 2, 3, 4, 5, and 6
respectively. A plot of the distribution of the minimum power of δ
greater than utmax/utmin for the cycles
where a=1 superimposed on the corresponding chi-square probability distribution with
2 degrees of freedom is;

A plot of the distribution of the minimum power of δ greater than
utmax/utmin for the cycles where a=2
superimposed on the corresponding chi-square distribution with 3 degrees of
freedom is;

A plot of the distribution of the minimum power of δ greater than
utmax/utmin for the cycles where a=3
superimposed on the corresponding chi-square distribution with 4 degrees of
freedom is;

A plot of the distribution of the minimum power of δ greater than
utmax/utmin for the cycles where a=4
superimposed on the corresponding chi-square distribution with 5 degrees of
freedom is;

A plot of the distribution of the minimum power of δ greater than
utmax/utmin for the cycles where a=5
superimposed on the corresponding chi-square distribution with 6 degrees of
freedom is;

A plot of the distribution of the minimum power of δ greater than
utmax/utmin for the cycles where
a=6 superimposed on the corresponding chi-square distribution with 7 degrees
of freedom is;

For a given a value, the distribution of the minimum power of δ
greater than utmax/utmin doesn't depend on
the upper bound of c very much.
Plots of the means of the distributions for a=1, 2, 3, ..., 10 and
cmax=1999, 3997, 5999, ..., 29999 are;

From bottom to top, the curves are for a equal 1 to 10. Plots
of the standard deviations of the distributions for a=1, 2, 3, 4, and 5
and cmax=1999, 3997, 5999, ..., 29999 are;

From bottom to top, the curves are for a equal 1 to 5. Plots
of the standard deviations of the distributions for a=6, 7, 8, 9, and 10
for cmax=1999, 3997, 5999, ..., 29999 are;

Plots of the sample sizes of the distributions for a=1, 2, 3, ..., 10
and cmax=997, 1999, 2999, ..., 99997 are;

The aberrant curve is for a=1. From top to bottom, the other
curves are for a equal 2 to 10 (the curves for a=2 and a=3
cross). The number of cycles having a given a value appears to
increase linearly with cmax (although the curve eventually
begins to resemble a step function).
The sample sizes for a=1, 2, 3, ..., 24 plotted against (cmax+1)/1000
or (cmax+3)/1000 for cmax=9997, 19999,
29999, ..., 199999 are;

A linear least-squares fit of the
curve for a=1 and cmax=997, 1999, 2999, ..., 99997
is;

p1=0.06089 with a 95% confidence interval of (0.05805,
0.06373) and p2=1640 with a 95% confidence interval of (1474,
1805). SSE=1.676e+007, R-square=0.9485, adjusted R-square=0.948, and
RMSE=413.6. A linear least-squares fit of the curve for a=2 and
cmax=997, 1999, 2999, ..., 99997 is;

p1=0.1691 with a 95% confidence interval of (0.1647, 0.1734) and
p2=1670 with a 95% confidence interval of (1418, 1922).
SSE=3.89e+007, R-square=0.9839, adjusted R-square=0.9838, and RMSE=630. A
linear least-squares fit of the curve for a=3 and cmax=997,
1999, 2999, ..., 99997 is;

p1=0.1959 with a 95% confidence interval of (0.1935, 0.1983) and
p2=336.9 with a 95% confidence interval of (196.5, 477.2).
SSE=1.208e+007, R-square=0.9962, adjusted R-square=0.9962, and RMSE=351.
Although a chi-square probability distribution doesn't model the distribution
very well for larger a values, the number of values in the right-hand
tails of the distributions is still about the same. For the 194664 cycles
for c less than or equal to 69997, there are 5463, 12533, 13505, 12072,
9941, 8240, 7103, 6118, 5521, and 4913 cycles where a equals 1, 2, 3,
..., and 10 respectively. A plot of the distribution of the minimum power
of δ greater than utmax/utmin for the
cycles where a=7 superimposed on the corresponding chi-square probability
distribution with 8 degrees of freedom is;

A plot of the distribution of the minimum power of δ greater than utmax/utmin
for the cycles where a=8 superimposed on the corresponding chi-square
probability distribution with 9 degrees of freedom is;

When the curve for the actual distribution rises more steeply than the curve for
the chi-square distribution (when a>7), there are fewer values in the
right-hand tail of the distribution than for the chi-square distribution.
A plot of the distribution of the minimum power of δ greater than utmax/utmin
for the cycles where a=9 superimposed on the corresponding chi-square
probability distribution with 10 degrees of freedom is;

A plot of the distribution of the minimum power of δ greater than utmax/utmin
for the cycles where a=10 superimposed on the corresponding chi-square
probability distribution with 11 degrees of freedom is;

Given the number of cycles for an
a value, the number of values of the smallest
power of δ greater than utmax/utmin
in the right-hand tail of the distribution can be estimated using the
chi-square distribution.
Proposition (27) then gives a relationship between the L-K
value of a cycle and an upper bound of utmax/utmin.
The Minimum |L-K| Value of the 3n+c Cycles for a Given c
Value
(c, L, K) values of cycles with no attachment points
where there are also no interrelated cycles with attachment points for c
less than or equal to 99997 are (1, 0, 1), (1, 1, 1), (1, 1, 2), (11, 1, 3),
(49, 1, 4), (179, 1, 5), (601, 1, 6), (1931, 1, 7), (6049, 1, 8), (18659, 1, 9),
(57001, 1, 10), (791, 2, 8), (85, 4, 8), (145, 4, 8), (57001, 1, 10), (2167, 4, 12), (66469, 3, 13), (8497, 4, 15), (29267, 4,
16), (53095, 4, 16), (16133, 12, 24), and (78313, 5, 19). These values are included in the following. For the c values less than or equal to 19999, there is only 1 cycle
(counting only one of interrelated cycles) for 2260 c values and the mean
and standard deviation of the L-K values are 1.013 and 21.245
respectively. A histogram of the L-K values superimposed on a
normal probability distribution having this mean and standard deviation is;

(There is a tendency for the L-K values to be a multiple of 6.)
For the c values less than or equal to 19999, there are exactly 2 cycles
(counting only one of interrelated cycles) for 2351 c values and the mean
and standard deviation of the L-K values of the smaller |L-K|
values are 0.185 and 11.385 respectively. A histogram of the L-K
values superimposed on the corresponding normal probability distribution is;

For the c values less than or equal to 19999, there are exactly 3
cycles (counting only one of interrelated cycles) for 1132 c values and
the mean and standard deviation of the L-K values of the smallest |L-K|
values are 0.281 and 7.669 respectively. A histogram of the L-K
values superimposed on the corresponding normal probability distribution is;

For the c values less than or equal to 19999, there are exactly 4
cycles (counting only one of interrelated cycles) for 452 c values and
the mean and standard deviation of the L-K values of the smallest |L-K|
values are -0.215 and 5.457 respectively. A histogram of the L-K
values superimposed on the corresponding normal probability distribution is;

The corresponding standard deviations when there are 5, 6, 7, and 8 cycles
(counting only one of interrelated cycles) are 4.195, 3.277, 3.109, and 2.515
respectively (when there are j cycles, the standard deviation is about 1/j
times the standard deviation when there is 1 cycle).
Plots of j times the standard deviation for j=1, 2, and 3
versus log(cmax) for cmax values of 997,
1999, 2999, ..., 99997 are;

Plots of j times the standard deviation for j=4, 5, 6, 7, and
8 versus log(cmax) for cmax values of 997,
1999, 2999, ..., 39997 are;

Plots of the proportions of c values having 1, 2, 3, 4, 5, and 6
cycles (counting only one of interrelated cycles) versus cmax
for cmax values of 997, 1999, 2999, ..., 49999 are;

For cmax=49999, an upper bound of the proportion of c values having only one cycle
is about 0.354 (the upper bound of the proportion may increase further as cmax
increases, but appears to be leveling off). For relatively small cmax values,
an upper bound of |L-K| can be computed beforehand using the
slope (about 4.74) and intercept (about -25.67) of the line giving the standard deviation of the distribution
of L-K values versus log(cmax).
A linear least-squares fit for cmax values up to 24997
when there is only one cycle is;

For example, the standard deviation for cmax=19999 should
be 21.272 (compared to the actual standard deviation of 21.245). There are
6667 c values less than or equal to 19999, so there should be less than
2360 (6667·0.354) c values with only one cycle (counting only one of
interrelated cycles). For a normal probability distribution with a mean of
0, a standard deviation of 21.272, and a sample size of 2360, the
expected number of L-K values becomes less than 1/2 for |L-K|>62.
In the actual distribution, the L-K values range from -112 to 108.
Out of the 2260 L-K values, 14 values are less than -62 and 13 values are greater
than 62. About 99% of the L-K values are then in the expected range.
The standard deviation of the L-K values of the smallest |L-K|
values doesn't increase linearly with log(cmax).
A cubic least-squares fit for cmax values up to
99997
when there is only one cycle (counting only one of interrelated cycles) is;

p1=0.1906 with a 95% confidence interval of (0.1675,
0.2136), p2=-4.622 with a 95% confidence interval of (-5.28,
-3.963), p3=41.51 with a 95% confidence interval of
(35.29, 47.73), and p4=-121.5 with a 95% confidence interval
of (-140.9, -102.2) . SSE=3.046, R-square=.9992,
adjusted R-square=.9992, and RMSE=0.1782. ( The adjusted R-square value for a
quadratic least-squares fit is .9968.) A quadratic least-squares fit of
the standard deviation of the L-K values when there is only
one cycle (counting only one of interrelated cycles) plotted against log(cmax)
for cmax=9997, 19999, 29999, ..., 199999 is;

p1=1.57 with a 95% confidence interval of (1.476, 1.665), p2=-25.25
with a 95% confidence interval of (-27.32, -23.19), and p3=117.2
with a 95% confidence interval of (106.1, 128.4). SSE=0.3439,
R-square=0.9997, adjusted R-square=0.9996, and RMSE=0.1422.
Let (L1, K1), (L2,
K2), (L3,
K3), ...,
(Ln, Kn) denote the (L, K)
values of the cycles for a given c value sorted by increasing L
values. For the c values less than or equal to 39997, the standard
deviations of the L-K values of the smallest |L-K|
values when (L1, K1), (L2,
K2), (L3, K3), ..., (Li,
Ki), i=1, 2, 3, ..., 7, are not included and
there are 2, 3, 4, ..., 8 cycles are as follows;
# cycles
2 3
4 5
6 7
8
i=1
28.617 14.938 9.807
7.066 5.640 4.343
3.372
2 n/a
26.498 14.273 8.897
7.540 5.456 3.876
3 n/a
n/a 25.309 14.022 10.020 6.825 5.020
4 n/a
n/a n/a
24.508 14.577 9.484
7.686
5 n/a
n/a n/a
n/a 23.872 14.445
9.315
6 n/a
n/a n/a
n/a n/a
24.387 13.634
7 n/a
n/a n/a
n/a n/a
n/a 18.637
When none of the (L, K) values are excluded, the standard
deviations of the L-K values of the smallest |L-K| values
for 1, 2, 3, ..., and 8 cycles are 26.214, 13.923, 9.465, 6.918, 5.316, 4.213,
3.336, and 3.007 respectively. For the c values less than or equal
to 99997, the standard deviations of the L-K values of the
smallest |L-K| values when (L1, K1),
(L2, K2), (L3, K3),
..., (Li, Ki), i=1, 2, 3, ..., 7,
are not included and there are 2, 3, 4, ..., 8 cycles are as follows;
# cycles 2 3 4 5
6 7 8
i=1 37.735 18.932 12.238 8.602 6.502
5.382 4.545
2 n/a 34.344 18.520 11.294 8.939
6.320 5.110
3 n/a n/a 31.834
16.662 12.025 8.160 6.014
4 n/a n/a n/a 30.582
17.415 11.584 7.892
5 n/a n/a n/a n/a
29.094 16.554 11.606
6 n/a n/a n/a n/a
n/a 32.073 18.093
7 n/a n/a n/a n/a
n/a n/a 32.363
When none of the (L, K) values are excluded, the standard
deviations of the L-K values of the smallest |L-K| values
for 1, 2, 3, ..., and 8 cycles are 34.620, 18.719, 12.196, 8.565, 6.482, 5.307,
4.256, and 3.966 respectively. For the c values less than or equal
to 199999, the standard deviations of the L-K values of the
smallest |L-K| values when (L1, K1),
(L2, K2), (L3, K3),
..., (Li, Ki), i=1, 2, 3, ..., 7,
are not included and there are 2, 3, 4, ..., 8 cycles are as follows;
# cycles 2 3 4 5
6 7 8
i=1
46.682 23.462 14.347 10.278 7.922
6.452 4.885
2 n/a
41.609 21.938 13.610 10.057 7.595 5.576
3 n/a n/a
38.775
20.521 13.873 9.730 6.622
4 n/a n/a n/a 35.499
20.758 13.006 8.901
5 n/a n/a n/a n/a
35.544 18.489 12.346
6 n/a n/a n/a n/a
n/a 34.944 18.806
7 n/a n/a n/a n/a
n/a n/a 34.597
When none of the (L, K) values are excluded, the standard
deviations of the L-K values of the smallest |L-K| values
for 1, 2, 3, ..., and 8 cycles are 43.014, 23.079, 15.069, 10.349, 7.923, 6.528,
5.402, and 4.150 respectively. Not including the sorted (L,
K) values does not change the standard deviations much.
A cubic least-squares fit of the standard deviations of the L-K
values when there are exactly two cycles and (L1, K1)
is excluded for cmax values up to 99997 is;

p1=0.1765 with a 95% confidence interval of (0.1543, 0.1987),
p2=-4.005 with a 95% confidence interval of (-4.64, -3.37), p3=33.87
with a 95% confidence interval of (27.88, 39.87), and p4=-90.65
with a 95% confidence interval of (-109.3, -71.98). SSE=2.833,
R-square=0.993, adjusted R-square=0.993, and RMSE=0.1718.
(L, K) Trees
Cycles for a given c value with (L, K) values that are
in arithmetic progression with an increment of (L1, K1)
(and aren't multiples of (L1, K1)) are said
to be associated with each other. For the 3333 c values less
than or equal to 9997, the numbers of c values having 1, 2, 3, ..., and
12 cycles (counting only one of interrelated or associated cycles) are 1115,
1319, 595, 186, 76, 31, 6, 2, 1, 0, 1, and 1 respectively. This
distribution has a mean of 1.0816. For a Poisson probability distribution
having this parameter, the expected numbers of c values having 1, 2, 3,
..., and 12 cycles are 1130, 1222, 611, 238, 64, 14, 3, 0, 0, 0, 0, and 0
respectively. For the 6667 c values less than or equal to
19999, the numbers of c values having 1, 2, 3, ..., and 12 cycles
(counting only one of interrelated or associated cycles) are 2260, 2618, 1152,
393, 161, 53, 17, 9, 2, 0, 1, and 1 respectively. This distribution has a
mean of 1.0817. For a Poisson probability distribution having this
parameter, the expected numbers of c values having 1, 2, 3, ..., and 12
cycles are 2260, 2445, 1322, 477, 129, 28, 5, 1, 0, 0, 0, and 0 respectively. For the
10000 c values less than or equal to 29999, the numbers of
c values having 1, 2, 3, ..., and 12 cycles (counting only one of interrelated
or associated cycles) are 3450, 3896, 1707, 597, 232, 72, 28, 11, 4, 0, 2, and 1
respectively. This distribution has a mean of 1.0697. For a Poisson
probability distribution having this parameter, the expected numbers of c
values having 1, 2, 3, ..., and 12 cycles are 3431, 3670, 1963, 700, 187, 40, 7, 1,
0, 0, 0, and 0 respectively. There are too many cycles for the
larger x values for the Poisson probability distribution to model the
actual distribution very well. (The number of c values having only
1 cycle is modeled fairly well though. For c less than or equal to
39997, there is only 1 cycle for 4681 c values, the distribution has a
mean of 1.0601, and the expected number of c values having only 1 cycle
is 4619. For c less than or equal to 49999, there is only 1 cycle
for 5909 cycles, the distribution has a mean of 1.0538, and the expected number
of c values having only 1 cycle is 5811.) (L, K)
trees (generalized
associated cycles) model the number of cycles better and are defined in
the Journal of Integer Sequences article (cycles with (L, K)
values that are in arithmetic progression with an increment of (L2,
K2) are also said to be associated with each other, etc.) .
For the c values less than or equal to 9997, the numbers of c
values having 1, 2, 3, ..., and 8 cycles (counting only one of interrelated
cycles or one of cycles in (L, K) trees) are 1115, 1338, 636, 178,
58, 6, 2, and 0 respectively. This distribution has a mean of
1.0255. For a Poisson probability distribution having this parameter, the
expected numbers of c values having 1, 2, 3, ..., and 8 cycles are 1195,
1226, 629, 215, 55, 11, and 2 respectively. For the c values less
than or equal to 1999, the numbers of c values having 1, 2, 3, ..., and 8
cycles (counting only one of interrelated cycles or one of cycles in (L,
K) trees) are 2260, 2664, 1228, 381, 117, 14, 3, and 0 respectively.
This distribution has a mean of 1.0228. For a Poisson probability
distribution having this parameter, the expected numbers of c values
having 1, 2, 3, ..., and 8 cycles are 2397, 2454, 1254, 428, 109, 22, 4, and 1
respectively. For the c values
less than or equal to 29999, the numbers of c values having 1, 2, 3, ...,
and 8 cycles (counting only one of interrelated cycles or one of cycles in (L,
K) trees) are 3450, 3980, 1805, 582, 158, 22, 3, and 0 respectively.
This distribution has a mean of 1.0096. For a Poisson probability
distribution having this parameter, the expected numbers of c values
having 1, 2, 3, ..., and 8 cycles are 3644, 3679, 1857, 625, 158, 32, 5, and 1
respectively.
For the c values less than or equal to 39997, the numbers of c
values having 1, 2, 3, ..., and 8 cycles (counting only one of interrelated
cycles or one of cycles in (L, K) trees) are 4681, 5273, 2369,
773, 205, 27, 5, and 0 respectively. This distribution has a mean of
0.9987. For a Poisson probability distribution having this parameter, the
expected numbers of c values having 1, 2, 3, ..., and 8 cycles are 4912,
4905, 2449, 815, 204, 41, 7, and 1 respectively. For the c
values less than or equal to 49999, the numbers of c values having 1, 2,
3, ..., and 8 cycles (counting only one of interrelated cycles or one of cycles
in (L, K) trees) are 5909, 6579, 2907, 970, 262, 35, 5, and 0
respectively. This distribution has a mean of 0.9933. For a Poisson
probability distribution having this parameter, the expected numbers of c
values having 1, 2, 3, ..., and 8 cycles are 6172, 6131, 3045, 1008, 250, 50, 8,
and 1 respectively. A plot of the distributions for c less
than or equal to 49999 is;

In this case, there are too few cycles for the larger x values but
the Poisson probability distribution still models the distribution fairly well.
For the c
values less than or equal to 199999, the numbers of c values having 1, 2,
3, ..., and 10 cycles (counting only one of interrelated cycles or one of cycles
in (L, K) trees) are 25074, 26248, 10797, 3486, 893, 137, 28, 2,
2, and 0
respectively. This distribution has a mean of 0.9413. For a Poisson
probability distribution having this parameter, the expected numbers of c
values having 1, 2, 3, ..., and 10 cycles are 26008, 24482, 11522, 3615, 851,
160, 25, 3, 0, and 0 respectively. The Poisson probability distribution
still models the distribution fairly well. The means of the distributions
plotted against (cmax+1)/1000 or (cmax+3)/1000
for cmax=9997, 19999, 29999, ..., 199999 are;

Another way to model the number of cycles is to count
only one of interrelated cycles, only one of associated cycles, and only one of
cycles where the (L, K) values are a multiple of another
common (L, K) value. Counting the number of cycles this way,
the numbers of c values for c less than or equal to 9997 having 1,
2, 3, ..., and 7 cycles are 1721, 1221, 318, 61, 11, 1, and 0 respectively.
This distribution has a mean of 0.6268. For a Poisson probability
distribution having this parameter, the expected numbers of cycles having 1, 2,
3, ..., and 7 cycles are 1781, 1116, 350, 73, 11, 1, and 0 respectively.
Counting the number of cycles this way, the numbers of c values for c
less than or equal to 19999 having 1, 2, 3, ..., and 7 cycles are 3501, 2408,
624, 108, 22, 3, and 1 respectively. This distribution has a mean of
0.6133. For a Poisson probability distribution having this parameter, the
expected numbers of cycles having 1, 2, 3, ..., and 7 cycles are 3611, 2214,
679, 139, 21, 3, and 0 respectively. Counting the number of cycles this way,
the numbers of c values for c less than or equal to 29999
having 1, 2, 3, ..., and 7 cycles are 5294, 3581, 937, 155, 28, 3, and 2
respectively. This distribution has a mean of 0.6059. For a Poisson
probability distribution having this parameter, the expected numbers of cycles
having 1, 2, 3, ..., and 7 cycles are 5456, 3306, 1001, 202, 31, 4, and 0
respectively. Counting the number of cycles this way, the numbers of c
values for c less than or equal to 39997 having 1, 2, 3, ..., and 7
cycles are 7124, 4765, 1196, 201, 40, 5, and 2 respectively. This
distribution has a mean of 0.5968. For a Poisson probability distribution
having this parameter, the expected numbers of cycles having 1, 2, 3, ..., and 7
cycles are 7341, 4381, 1307, 260, 39, 5, and 0 respectively. Counting the
number of cycles this way, the numbers of c values for c less than
or equal to 49999 having 1, 2, 3, ..., and 7 cycles are 8925, 5963, 1461, 259,
49, 8, and 2 respectively. This distribution has a mean of 0.5946.
For a Poisson probability distribution having this parameter, the expected
numbers of cycles having 1, 2, 3, ..., and 7 cycles are 9197, 5468, 1626, 322,
48, 6, and 1 respectively. (The numbers of cycles for the larger x
values are modeled better.) A plot of the distributions for c less
than or equal to 49999 is;

For large upper bounds of c values (such as 199999), this approach
doesn't model the number of cycles very well; there are too few cycles for the
larger x values. For cmax=199999, the numbers of cycles are 36517, 23653, 5268, 958,
193, 51, 17, 3, 2, and 0 respectively and the expected numbers of cycles are
37568, 21544, 6178, 1181, 169, 19, 2, 0, 0, and 0 respectively.
The Number of Prime Factors of 2K+L-3K
The number of prime factors of a natural number n where the prime
factors are not necessarily distinct is denoted by Ω(n). For 1≤L,
K≤29, the numbers of values of 2K+L-3K
where Ω(|2K+L-3K|) equals 1, 2, 3, 4,
5, 6, 7, and 8 are 117, 267, 229, 119, 63, 30, 8, and 6 respectively (there are no
prime factors of 2K+L-3K
in two instances, so the number of samples is 839 [292-2]).
A Poisson probability distribution where λ=1.8760 can be used to model this
data. A plot of the data superimposed on a Poisson probability
distribution having the same mean (where the numbers of values are counted as
being 0, 1, 2, 3, 4, 5, 6, and 7) is;

Corresponding data for smaller L, K upper bounds is;
# prime factors=
1 2 3
4 5 6
7 8
L,
K upper bound=2 2
3 7
4 11 2
1
5 17 5
1
6 19 11
4
7 26 16
5
8 29 21
11 1
9 36 27
15 1
10 37 36 22
3
11 46 46 23
4
12 48 54 28
8 3 1
13 54 65 36
8 3 1
14 56 75 41
17 4 1
15 58 90 48
21 5 1
16 61 100 54
28 7 4
17 67 113 66
29 8 4
18 67 121 76
36 14 8
19 75 133 87
40 15 9
20 76 144 97
47 22 11 0
1
21 83 157
108 55 24 11
0 1
22 83 166 124 68
27 13 0
1
23 90 185 133 75
30 13 0
1
24 91 192 148 79
38 18 3
5
25 98 209 164 84
42 18 3
5
26 101 219 179 95 50
22 3 5
27 107 229 201 104 55
22 4 5
28 113 240 210 113 62
30 8 6
A plot of the means of these distributions is;

Corresponding Poisson probability distributions model the number of prime
factors fairly well. A linear least-squares fit of the means plotted
against the logarithm of the maximum L, K value is;

p1=0.8852 with a 95% confidence interval of (0.838, 0.9324)
and p2=-1.111 with a 95% confidence interval of (-1.24,
-0.9823). SSE=0.09954, R-square=0.9842, adjusted R-square=0.9836, and
RMSE=0.0644. The number of prime factors of 2K+L-3K
affects the number of c values covered by the parity vectors
corresponding to (K+L, K).
More on the Domain of 3n+c Cycles
In the following,
all cycles are assumed to have been found for c values up to certain
limits. For the c values less than 1000, at least one primitive
cycle where a>1 occurs for every c value except 1, 7, and 37.
The largest domain of the absolute values of the u values and the
absolute values of their proxies occurs for a cycle for c=5; the
domain is (-2.027326e-001, 3.465736e-001). The domains of the cycles for
most c values are one, two, or three orders of magnitude smaller.
For the c values less than 1000, the smallest domain occurs for a cycle
for c=467; the domain is (-1.051072e-007, 1.944498e-007). Small
domains also occur for cycles for c=311 and c=343 (and other c
values). The smallest domains for cycles for larger c values appear
to become increasingly smaller. For example, for c=4501, nine
primitive cycles where a>1 occur and the domains are as large as
(-3.956808e-004, 1.654824e-003) and as small as (-7.278549e-008, 2.117179e-007).
When the domain of the absolute values of the u values and the absolute
values of their proxies is
small, the (K+L, K) value of the cycle is likely to be a generalized
continued-fraction convergent of log(3)/log(2). (Even for the c=1
cycle, the (K+L, K) value [(11, 7)] is a generalized
continued-fraction convergent of log(3)/log(2).) For example, when c=467,
the (K+L, K) value is (84, 53), a continued-fraction convergent of
log(3)/log(2). When c=311, the (K+L, K) value is (19,
12), a continued-fraction convergent of log(3)/log(2). When c=343,
the (K+L, K) value is (149, 94), a generalized continued-fraction
convergent of log(3)/log(2). When the domain is small, (K+L, K)
values that are small multiples (usually 2) of generalized continued-fraction
convergents of log(3)/log(2) occur. For example, when c=4501, the (K+L,
K) value is (92, 58), twice a generalized continued-fraction convergent
of log(3)/log(2). When the domain is small, (K+L, K) values
that are approximately equal to generalized continued-fraction convergents of
log(3)/log(2) occur. For example, for a cycle for c=407, the (K+L,
K) value is (44, 28), almost equal to a generalized continued-fraction
convergent ((46, 29)) of log(3)/log(2). However, cycles occur for some
c values where the domain appears to be small but there is no apparent
relationship between the (K+L, K) values and the generalized
continued-fraction convergents of log(3)/log(2). This occurs for a cycle
for c=1813 where the domain is (-7.915834e-007, 3.418000e-006) and the (K+L,
K) value is (228, 132) and for a cycle for c=2009 where the domain
is (-4.947314e-006, 1.590942e-005) and the (K+L, K) value is (175,
98). The (K+L, K) values are fairly large multiples of
approximations of generalized continued-fraction convergents of log(3)/log(2).
The domains are no longer "small" for all of the cycles of these large c
values.
Extended Sequences of 3n+c Cycles
In this section, the element after an odd element i is defined to be
3i+c. The shortest possible jump from an odd element in the
3n+c sequence to another odd
element will be referred to as a "hop" (when the element after an odd element
i is defined to be 3i+c, there are two even elements between
the initial odd element and the destination of the jump). An example of a "multiple-jump" attachment point (for
c=11) is -21→-13→-7→-1, 8. The attachment point is several jumps away
from the odd integer divisible by 3, that is, -21 jumps to -13, -13 jumps to -7,
-7 jumps to -1, and 8 immediately follows -1. The jumps in multiple-jump attachment points usually consist of a
jump followed by one or more hops or one or more hops followed by a jump.
On average, there are 1.2 jumps and 2.0 hops in a multiple-jump (based on the
3767 multiple-jump attachment points for the c values less than or equal
to 1999). One-jump attachment points (such as -21→-23, -68 [for c=1])
have some special properties.
An example of a "jumped-over" attachment point (for c=13) is 51→358.
The destination of the jump is not the attachment point associated with the odd
integer divisible by 3; the attachment point (262 in this case) has been "jumped
over". Empirical results are;
(32) The destination of a jumped-over attachment point is another
attachment point if the destination is even.
(33) The sign in an extended sequence can change only once.
If the sign in the extended sequence of a jumped-over attachment point changes,
it usually does so at the attachment point. For example, -63→74 for a
cycle for c=95 where the attachment point 26 is jumped over. The
extended sequence up to 26 is {-63, -94, -47, -46, -23, 26}. Sometimes
there are several jumps before the attachment point is jumped over. For
example, -249→-287→-173→-89→118 for a cycle for c=169 where the
attachment point 22 is jumped over. The sequence up to 22 (starting with
-89) is {-89, -98, -49, 22}. Jumped-over attachment points become rare
when the domain of the absolute values of the u values and the absolute values of their
proxies becomes small. As will be shown (by way of empirical evidence),
the largest possible li value (in the chain equation) in a 3n+1
cycle (n>0) without a jumped-over attachment point is 5. (Of
course, determining whether jumped-over attachment
points cease to exist for a sufficiently small domain
would be difficult.)
An example of a "no-jump" attachment point
(for c=11) is -3, 2. The odd integer divisible by 3 is immediately
before the attachment point. Empirical results are;
(34) In a cycle having an attachment point, there is at least one no-jump
or one-jump attachment point.
(35) In primary, secondary, tertiary, etc., attachment points, the
types of attachment points that can occur have a specific order; a no-jump
attachment point (not necessarily the primary attachment point) is followed by a
jumped-over attachment point, the jumped-over attachment point is followed by a
multiple-jump (or one-jump) attachment point, the multiple-jump (or one-jump) attachment point is
followed by a no-jump attachment point, etc.
(36) Except when the last attachment point in primary, secondary, tertiary,
etc., attachment points is a jumped-over attachment point, the destination of a
jumped-over attachment point is the next attachment point.
(37) A jumped-over attachment point cannot be a primary attachment point.
In the chain equation, the element after an odd element i in the 3n+1
sequence (n>0) is defined to be (3i+1)/2. Counting the
even element before a primary attachment point and the even elements up to the
tertiary attachment point gives 6 even elements. If there are primary,
secondary, and tertiary attachment points in a cycle, one of them must be a jumped-over
attachment point (by Proposition (35)).
Solving for a one-jump attachment point followed by a no-jump attachment point
(in primary, secondary, tertiary, etc., attachment points) gives the Diophantine equation (3/2)h=(8t2+3c)/(t1+c)
where 2h is the largest power of 2 that divides t1+c.
Solving for a no-jump attachment point followed by a jumped-over attachment
point gives (3/2)i=(3/8)(t2+3c)/(t3+c)
(usually, 2i is not the largest power of 2 that divides t3+c).
Solving for a jumped-over attachment point followed by a one-jump attachment
point gives (3/2)i-j=3(t4+c)/(t3+c),
etc.
Hardy and Littlewood13 proved that the sequence {frac(xn)}
where frac(x) is the fractional part of x is equidistributed for
almost all real numbers x>1 (the exceptional set has Lesbeque measure
zero). (A sequence of real numbers {xn} is
equidistributed on an interval [a, b] if the probability of
finding xn in any subinterval is proportional to the
subinterval length. The points of an equidistributed sequence form a dense
set on the interval [a, b].) The properties of {frac(3/2)n}
have been extensively studied. Since {frac(3/2)n}
appears to be equidistributed (and thus dense), the equation (3/2)h=(8t2+3c)/(t1+c)
(or one of the other equations) is likely to have many solutions (as can be
easily verified).
The exponents of 3/2 in the above equations are small. For example, for c=41, the attachment points for primary, secondary, tertiary, and
quatenary attachment points for a cycle are 3→29, 128 (a one-jump attachment
point), -3, 32 (a no-jump attachment point), -21→2 (an attachment point where 8
is jumped over [the sequence up to 8 is {-21, -22, -11, 8}]), and
-87→-55→-31→-13, 2 (a multiple-jump attachment point). The last attachment
point is not a one-jump attachment point, but -31 can be substituted for t4
in the equation above. t1=3, t2=-3,
and t3=-21 and the values of h, i, and j
are 2, 2, and 1 respectively. For c=137, there are primary,
secondary, tertiary, and quatenary attachment points for a cycle (starting with
a one-jump attachment point) and the successive exponents of 3/2 are 4, 2, and
1. For c=107, there are primary, secondary, tertiary, etc.,
attachment points for a cycle (starting with a no-jump attachment point) and the
successive exponents of 3/2 are 2, 1, 1, and 3. For c=4159, there
are primary, secondary, tertiary, etc., attachment points for a cycle (starting
with a one-jump attachment point) and the successive exponents of 3/2 are 1, 3,
2, 2, 2, and 1. For c=4519, there are primary, secondary, tertiary,
etc. attachment points for a cycle (starting with a one-jump attachment point)
and the successive exponents of 3/2 are 2, 2, 1, 1, 2, and 1. When there
are more than three attachment points in primary, secondary, tertiary, etc.,
attachments points, the attachment points are frequently powers of 2 (for c≤151,
the only exception occurs for the above cycle for c=137).
Another empirical result is;
(38) The last attachment point in the group of primary, secondary,
tertiary, etc., attachment points preceding a primary multiple-jump attachment
point is a no-jump or jumped-over attachment point.
A Diophantine equation (similar in form to those derived for primary, secondary,
tertiary, etc., attachment points) involving the t value of a
multiple-jump attachment point (or at least the odd element at the beginning of
the last jump of the multiple-jump) and the t value of the preceding no-jump
or jumped-over attachment point can be derived.
The Simplified Structure of a 3n+c Cycle Having Attachment Points
Another empirical result is;
(39) A primary attachment point is a multiple-jump attachment point only
if the attachment point is one jump away from the first odd cycle element after
the preceding primary attachment point.
A consequence of the above proposition (and Proposition (37)) is that a u
value jumps (in one jump) to the next primary
attachment point, or if its proxy isn't the odd integer immediately before the
next primary attachment point, the proxy jumps (in one jump) to the odd integer
immediately before the next primary attachment point, etc. This is the
aforementioned simplified structure of a cycle.
The Largest Power of 2 That Divides the Difference Between a u Value
and Its Proxy
Let 2j be the
largest power of 2 that divides the difference between a u value and its
proxy. Empirical results are;
(40) For a one-jump attachment point that is a primary attachment point, the expected value of j+1 is
the number of odd
elements in the jump (counting the destination of the jump).
(41) For a multiple-jump attachment point that is a primary attachment
point, j is small (the numbers of j values equal to 1, 2, 3, 4, 5,
and 6 for the c values less than or equal to 997 are 555, 447, 82, 9, 1,
and 1 respectively).
There is usually a one-jump
attachment point in a cycle where j or j+1 equals the number of
odd elements in the jump. (For the c=1 cycle, -21≡-17(mod 22) and there are 3 odd
elements in the jump.) For example, when c=3013, there are 93 primitive cycles (with a total of 338
attachment points) having an (K+L, K) value of (38, 24) (a
generalized continued-fraction convergent of log(3)/log(2)). For 72 of the 202
primary one-jump attachment points,
j+1 equals the number of
odd elements in the jump and for 48 of the primary one-jump attachment points, j
equals the number of odd elements in the jump. A histogram of the differences between the number of odd
elements in the jump and j is;

More on the Chain Equation
Note that the modulo operations (u≡t(mod 2j))
introduce variables corresponding to the ai values in the
chain equation (in the chain equation, xi≡-1(mod 2k(i))
where xi is a local minimum). Similarly, the odd
integers before the attachment points in no-jump attachments points correspond
to ai values so that there are the same number of variables as
in the chain equation. From this
perspective, the c=1 cycle is a 1-cycle. [The variables of the
chain equation are k0=4, l0=1, a0=-1,
k1=3, l1=3, and a1=-5.]) However, these equations don't have
the same form as the chain equation (except for multiple-jump attachment points
where the usual "path" is taken) since, for a one-jump attachment point, the attachment point equals 3i+c
where i is the destination of the jump. Similarly, these equations don't
have the same form as the chain equation for no-jump attachment points.
Simons and de Weger show that all xi are about the same size
by "chaining" them. Their Lemma 6 is;
For all i = 0,1,..., m-1
we have xi+1 < bδxiδ
where b = (1 + X0-1)/21/δ
and X0 is a lower bound of xmin.
For a one-jump attachment point, the next u value equals {[(3/2)f+1(t+c)-(c/2)]/2}/2g
where 2f is the largest power of 2 that divides t+c.
This expression is less than (1/2)(3/2)f+1(t+c)=(1/2)(2f+1)δ-1(t+c).
If u and t are positive,
t=2ja+u where a≥1, so the next u
value is less than (1/2)[2f+1-j(2ja+u+c)]δ-1(t+c)=(2f+1-j)δ-1(1/2)(t+c)δ.
So if u and t are positive and f+1 (the number of odd elements in the jump [counting the
destination of the jump]) is less than or equal to j, a result analogous
to Lemma 6 can be derived (where b=(1+cX0-1)/21/δ
and X0 is a lower bound for tmin).
For a no-jump attachment point, the next u value equals [(3/2)(t+c)-c]/2g.
This expression is less than (1/2)(3/2)(t+c), so if u and
t are positive, a result analogous to Lemma 6 can be derived. For a multiple-jump attachment point consisting of a jump followed by a hop,
the odd element immediately before the attachment point is [(3/2)f+1(t+c)-(c/2)]/22.
The next u value then equals {[(3/2)f+2(t+c)+(5/4)c]/22}/2g.
This expression is not necessarily less than (1/2)(3/2)f+2(t+c).
For a multiple-jump attachment point consisting of a jump followed by two hops,
the next u value equals {[(3/2)f+3(t+c)+(47/8)c]/23}/2g.
Simons and de Weger's Lemma 7 (derived from Lemma 6 and Corollary 5) is;
0 < Λ < mcm2-((δ
-1)/ζ)K
where cm=
2(m/δ)(δ -1)/ζbδ/(δ-1)-m/ζ
and ζ denotes δm-1. (The symbol
ζ is used due to typographical difficulties.) Simons and de Weger's Lemma 14 (their main result) is;
Let x=K1(m) be the largest solution of
e-13.3(0.46057+log x)=mcm2-((δ
-1)/ζ)x.
Then K<K1(m).
Complementary Variables
The expected number of odd elements in the jump (or jumps in the case of a
multiple-jump attachment point) from t to the odd integer before a
primary attachment point (including the destination of the jump or t in
the case of a no-jump attachment point) is the number of even elements after the even element immediately before
the primary attachment point
(including the even element) plus the
number of jumps (none for a no-jump attachment point, 1 for a one-jump
attachment point, and at least 2 for a multiple-jump attachment point) minus the number of hops between u
and the primary attachment point. For example, for the c=1 cycle, there are 3 odds
elements in the jump from -21 to -23, the even elements are -136,
-68, and -34, and the hop between -17 and -68 is {-55, -164, -82, -41} (3=3+1-1). A
histogram of the number of odd elements in the jump (or jumps) from t to
the odd integer before the primary attachment point minus the number of jumps plus the number
of hops between u and the primary attachment point minus the number of even elements after the even element
before the primary
attachment point for the 22851 primary attachment points for the c values less than or equal to
1999 superimposed on a normal probability distribution having the same
parameters is;

The mean of the distribution is -0.004901 and the standard deviation is 2.3789.
Other than being discrete-valued, the distribution resembles a normal probability distribution
for small cmax values.
For c values less than or equal to 49, the mean is 0.5319 with a 95% confidence
interval of (0.1571, 0.9067) and the standard deviation is 1.8299 with a 95%
confidence interval of (1.6005, 2.1367). A normal probability plot
of the data is;

For c values less than or equal to 199, the mean is 0.3458 with a 95%
confidence interval of (0.1694, 0.5221) and the standard deviation is
2.4152 with a 95% confidence interval of (2.2968, 2.5466). A normal
probability plot of the data is;

A histogram of the number of odd elements in the jump (or jumps) from t
to the odd integer before the primary attachment point minus the number of jumps
plus the number of hops between u and the primary attachment point minus
the number of even elements after the even element before the primary attachment
point for the 36112285 primary attachment points for the c values less
than or equal to 199999 superimposed on a normal probability distribution having
the same parameters is;

This distribution has a mean of -0.1381 and a standard deviation of 2.3462.
A plot of the standard deviations of the distributions versus cmax for
cmax=9997, 1999, 2999, ..., 199999 is;

The distributions appear to be tending towards a fixed probability distribution.
A histogram of the sum of the number of odd elements in the jumps from t
values to the odd elements before the primary attachment points minus the sum of the number
of jumps plus the number
of hops in the cycle minus the sum of the number of even elements after the even
element before the primary attachment points for the 3213
cycles less than or equal to 1999 is;

The above distribution has a mean of -0.03486 and a standard deviation of
6.1492. The number of odd elements in the jumps from t to the odd
element before a primary attachment point and the number of even elements after
the even element before the primary attachment point are "complementary"
variables. A histogram of the sum of the number of odd elements in
the jumps from the t values to odd elements before the primary attachment
points minus the sum of the number of even elements after even elements before
the primary attachment points for the 3213 cycles less than or equal to 1999 is;

The above distribution has a mean of -0.4591 and a standard deviation of
6.6471. A quadratic least-squares fit of the standard deviations of these
distributions plotted against log(cmax)
for cmax=9997, 19999, 29999, ..., 199999 is;

p1=0.8128 with a 95% confidence interval of (0.6758, 0.9497),
p2=-12.93 with a 95% confidence interval of (-15.92, -9.95),
and p3=59.63 with a 95% confidence interval of (43.45, 75.8).
SSE=0.7203, R-square-0.9975, adjusted R-square=0.9972, and RMSE=0.2058. A
quadratic least-squares fit of the means of these distributions plotted against
log(cmax) for cmax=9997, 19999, 29999, ...,
199999 is;

p1=0.01189 with a 95% confidence interval of (0.008548,
0.1524), p2=-0.5579 with a 95% confidence interval of
(-0.6302, -0.4855), and p3=-1.275 with a 95% confidence
interval of (-1.605, -0.9451). SSE=0.7506, R-square=0.9887, adjusted
R-square=0.9874, and RMSE=0.2101.
The number of jumps from t to the odd element before a
primary attachment point and the number of hops between the corresponding u
value and the primary attachment point are complementary variables. A histogram of the number of hops in the cycle minus the sum of the number
of jumps from t values to the odd elements before the primary attachment
points for the 3213 cycles less than or equal to 1999 is;

The above distribution has a mean of 0.4242 and a standard deviation of
5.2375. A quadratic least-squares fit of the standard deviations of the
distributions plotted against log(cmax) for cmax
=9997, 19999, 29999, ..., 199999 is;

p1=0.2415 with a 95% confidence interval of (0.2038, 0.2793),
p2=-2.73 with a 95% confidence interval of (-3.552, -1.908),
and p3=11.83 with a 95% confidence interval of (7.368, 16.28).
SSE=0.0547, R-square=0.9993, adjusted R-square=0.9992, and RMSE=0.05672.
The means of the distributions are approximately equal to 0.
Chaining u Values Together and Chaining t Values Together
Let n denote the number of jumps in the multiple-jump of a primary
multiple-jump attachment point. Also, let n equal 1 for a primary
one-jump attachment point and let n equal 0 for a primary no-jump
attachment point. Let h denote the number of hops between u and the primary
attachment point, let f denote the number of odd elements in the jump (or
jumps) from t to the odd element immediately before the attachment point
(let f equal 0 for a no-jump attachment point), and let g denote the number of even elements after the even element
before the primary attachment point. As previously shown, {[(3/2)f+1(t+c)]/2n}/2g
is less than the next u value for no-jump and one-jump attachment points
and greater than the next u value for multiple-jump attachment points.
Assuming these deficiencies and excesses cancel out, ∏{[(3/2)f(i)+1(ti+c)]/2n(i)}/2g(i)
is approximately equal to ∏ui where the product is from i=1
to a. [2∑(f(i)+1)-∑j(i)]δ-1/2∑g(i)
is usually less than 1, so if the u and t values are positive,
∏(ti+c )δ/2n(i)
should be greater than ∏ui.
(Of the 3212 cycles for the c values less than or equal to 1999, [2∑(f(i)+1)-∑j(i)]δ-1/2∑g(i)
is greater than 1 in only 37 instances and its largest value is 17.31905.) In proving Lemma 6, Simons and de Weger show that (1/2)(xi+1)δ>xi+1.
Similarly, if the u values are positive, (1/2)(ui+c)δ is greater
than the next local minimum (possibly the destination of a hop). An
empirical result is;
(42) The u values can be chained together, that is, |ui+c|δ
is almost always greater than |ui+1|. The
corresponding t values can be chained together, that is, 2n(i)|ti+c|δ
is almost always greater than |ti-1|.
Also, 2n(i)|ti+c|δ
is almost always greater than |ui+1|. (The u and t values are indexed circularly.)
Note that there are no restrictions on the signs of the u and t
values in the above proposition. Of
the 22843 primary attachment points of the c values less than or equal to
1999, the chain of u values is broken only 23 times (in every
instance, the next primary attachment point doesn't have an associated secondary
attachment point). Of the 22843 primary attachment points of the c values less
than or equal to 1999, the chain of proxies is broken only 47 times. The
t value of a primary multiple-jump attachment point where the multiple-jump
consists of two jumps, two hops, or a jump and a hop can be chained (without scaling
by a factor of 22) with the
t value of the preceding attachment point (not necessarily primary).
(If |t+c|=2h, then the absolute value of the
preceding t value equals 3h [an empirical result] so
that |t+c|δ equals the absolute value of the
preceding t value.) Chaining
one of these t values to the t value of the preceding primary
attachment point is then apt to fail (even after scaling by a factor of 22) when the preceding
primary attachment point has associated secondary, tertiary, quatenary, etc.
attachment points. This accounts for 38 out of the 47 instances where the
chain of proxies is broken. In 3 other instances, the t value of a
primary one-jump attachment point can't be chained to the t value of the
preceding primary attachment point. This occurs when the preceding primary
attachment point has associated secondary and tertiary (and quatenary)
attachment points. Of the 22843 primary attachment points of the
c values less than or equal to 1999, 2n(i)|ti+c|δ
is less than |ui+1| in 99 instances and 96 of these
instances occur when the multiple jump of a primary multiple-jump
attachment point consists of two jumps, two hops, or a jump and a hop.
The
corresponding definition of b in Lemma 6 is b=|1+cX0-1|
where X0 is multiple-valued, that is, if u or t
is positive, then u or t is greater than X0, or
if u or t is negative, then u or t is less than
-X0. (Note that b=1+cX0-1
or |1-cX0-1|.) m-cycles then become
a-cycles. ca is then defined so that |1+cX0-1|ab(δ/(δ-1))(ζ/(δ-1)-a)=caζ/(δ-1),
that is, ca=bδ/(δ-1)-a/ζ
where ζ denotes δa-1. ∑(1/|ui|+1/|ti|)
where the summation is from i=1 to a is less than a/umin+a/tmin,
so the corresponding version of Lemma 7 (empirically derived) is;
(43) |Λ|<5caca2-((δ-1)/ζ)K
X0 can be defined to be the smallest |u| or |t|
value in the cycle or an empirically derived lower bound of the minimum.
For the c=121 cycle, L=42, K=46, a=10, the
largest negative proxy value is -9, the smallest positive proxy value is 21, and
the smallest u value is 19. Λ equals 10.46078661. Assuming
this is the only c=121 10-cycle in existence, X0 can be
set to 9. b then equals 14.44444444 or 12.44444444. ca
then equals 1059.577577 or 718.2799973. 5caca2-((δ-1)/ζ)K
then equals 5310117 or 359969.
This test (where X0 is set to the smallest |u| or |t|
value in the cycle) fails for 489 of the 663743 cycles with attachment points for the
c values less than or equal to 199999. In almost every case, the (K+L,
K) value of the cycle is approximately equal to the (K+L, K)
value of an M-cycle generated from the parity vector p and a is small.
In every case, L<K and a≤10. Usually (in all but 45
cases), the cycle
is a 1-cycle where the inequality simplifies to |Λ|<5cb2-K.
Setting the X0 value to 17 for the c=1 cycle gives 5cb2-K equals 0.04136029
or 0.03676471 (Λ=-0.06566703). Denote the (L,
K) value of a cycle generated from the parity vector p by (L',
K'). If the (L, K) value of a cycle doesn't equal that
of an M-cycle generated from the parity vector p, but K=K'
for some K', set d to L'-L, otherwise set d
to zero. If K≠K' for any K' then set d
to L'-L where L' corresponds to the first K'
>K. A histogram of the d values for the cycles where a≠1
is;

In two instances, the d value is negative. A histogram
of the d values for the cycles where a=1 is;

The (c, L, K, a, utmin) values
for the exceptions when a≠1 are (295, 12, 18, 2, 281), (679, 24, 36, 5,
669), (2381, 20, 30, 5, 2349), (2647, 23, 32, 4, 2589), (3221, 14, 21, 2, 3187),
(3623, 15, 23, 3, 3609), (4741, 13, 19, 2, 4743), (6511, 15, 22, 2, 6441),
(6661, 23, 33, 5, 6621), (9145, 20, 30, 3, 9171), (12769, 21, 28, 3, 12699),
(13085, 12, 18, 3, 13123), (16105, 14, 21, 4, 16083), (17753, 16, 24, 4, 17751),
(22885, 24, 38, 6, 22859), (24817, 15, 21, 2, 25083), (27713, 38, 62, 10,
27753), (31727, 14, 23, 4, 31713), (33313, 9, 12, 3, 33303), (37465, 12, 18, 2,
37479), (42665, 16, 40, 3, 43689), (50857, 9, 30, 2, 52393), (58045, 12, 16, 3,
58117), (71873, 16, 14, 2, 72041), (71873, 16, 24, 3, 71899), (72023, 14, 20, 4,
72073), (73811, 20, 30, 6, 74013), (73811, 20, 30, 5, 73901), (82955, 12, 16, 2,
82827), (86233, 24, 36, 4, 86515), (103427, 8, 12, 2, 103395), (104551, 39, 60,
9, 104845), (108521, 22, 34, 4, 108487), (116449, 20, 28, 5, 1166871), (127735,
16, 24, 5, 127593), (130955, 20, 30, 4, 130827), (130955, 20, 30, 5, 130969),
(138503, 14, 21, 2, 138173), (138503, 14, 21, 3, 138609), (145201, 23, 38, 5,
145359), (154403, 12, 18, 2, 154365), (154403, 12, 18, 4, 154395), (159523, 24,
36, 5, 159387), (172555, 14, 21, 3, 172713), and (192685, 16, 24, 192191).
In every instance, the test passes when b
is set to 1+cX0-1 and fails when b is set to
|1-cX0-1| (the respective values of 5caca2-((δ-1)/ζ)K
in the latter case are 0.3691, 0.3922, 1.4575, 2.7252, 0.2127, 0.1860, 0.0061,
0.3373, 0.6257, 0.1063, 0.6044, 0.8059, 0.1618, 0.0011, 0.0397, 1.6251, 0.0417,
0.0299, 0.0977, 0.0529, 4.6475, 1.2214, 1.1050, 0.2577, 0.0566, 0.2069, 1.1974,
0.2520, 1.4361, 1.5065, 0.5626, 0.9057, 0.0226, 1.2505, 0.4705, 0.3435, 0.0024,
1.1474, 0.5873, 0.2706, 0.1224, 0.0032, 0.1931, 0.9929, and 0.7907 and the respective values of |Λ| are
1.0194, 2.0388, 1.6990, 2.9675, 1.1893, 1.0715, 1.3071, 1.4770, 2.5620, 1.6990,
3.2031, 1.0194, 1.1893, 1.3592, 1.2279, 1.8824, 1.2008, 0.3784, 1.3727, 1.0194,
5.1282, 5.9256, 1.8303, 1.3592, 1.3592, 1.5948, 1.6990, 1.6990, 1.8303, 2.0388,
0.6796, 2.7048, 1.4634, 2.5099, 1.3592, 1.6990, 1.6990, 1.1893, 1.1893, 0.5347,
1.0194, 1.0194, 2.0388, 1.1893, and 1.3592). In every instance, the
smallest |u| or |t| value in the cycle is approximately equal to
c. A plot of c versus utmin is;

A plot of the relative errors is;

The two large negative spikes in the middle of the graph correspond to the two
negative d values in a previous graph. A similar relationship
between c and utmin is not valid for exceptions when
a=1.
When only umin is considered (and a factor of 16.0 is used
instead of 5.0), the inequality fails for 359 of the cycles for c≤199999.
In all but 72 instances, the cycle is a 1-cycle. In every instance, L<K
and a≤13. A histogram of the d values for a≠1 is;

Only one value is negative. A histogram of the d values when a=1
is;

A plot of c versus umin is;

A plot of the relative errors is;

The large negative spike in the middle of the graph corresponds to the
negative d value in a previous graph.
When only tmin
is considered (and a factor or 128.0 is used), the inequality fails for 140 of
the cycles where c≤199999. In all but 12 cycles, the cycle is a
1-cycle. In every instance L≤K and a≤13. A histogram
of the d values for a≠1 is;

A histogram of the d values for a=1 is;

A plot of c versus tmin is;

For a linear least-squares fit of the curve, the slope is 0.9996 with a 95%
confidence interval of (0.9993, 1), the intercept is 10.85 with a 95% confidence
interval of (-14.19, 35.9), and R-squared=1. A plot of the relative errors
is;

Local Maximum and Minimum Odd Elements in a 3n+c Cycle
Let locmin
denote the odd element between two successive primary attachment points
having the smallest absolute value. Usually, for a
one-jump attachment point,
locmin equals u or is a few successive hops away from u. For the
4234
primary one-jump attachment points for the c values less
than or equal to 997, the numbers of attachment points where 0, 1, 2, 3, 4, 5,
and 6 hops are required to reach locmin are 3677, 358, 102, 19, 5, 1, and 0
respectively. For 72 of the attachment points, locmin can't be
reached by successive hops away from u. These proportions
don't change much for different c upper bounds; a table of proportions
where i denotes the number of hops and n denotes the number of
primary one-jump attachment points is;
cmax= 49999 99997 149999 199999
i=0 9.087466e-001 9.103450e-001 9.108970e-001 9.111167e-001
1 6.377740e-002 6.288359e-002 6.253354e-002 6.238482e-002
2 1.576506e-002 1.560997e-002 1.560444e-002 1.560868e-002
3 4.056629e-003 3.968739e-003 3.938980e-003 3.916318e-003
4 9.995667e-004 9.866914e-004 9.902790e-004 9.858214e-004
5 2.581761e-004 2.566830e-004 2.553726e-004 2.519073e-004
6 6.479131e-005 6.738539e-005 6.547580e-005 6.579589e-005
7 1.088098e-005 1.285856e-005 1.365493e-005 1.372299e-005
8 0.000000e+000 9.765999e-007 2.544396e-006 2.819064e-006
9 4.945902e-007 4.882999e-007 5.936925e-007 6.382787e-007
10 0.000000e+000 0.000000e+000 8.481321e-008 5.318989e-008
- 6.320368e-003 5.867575e-003 5.698006e-003 5.652702e-003
n= 2021876 6143765 11790616 18800566
Let locmax
denote the odd element between two successive primary attachment points having
the largest absolute value. Let i denote the last odd element
before the second primary attachment point. If locmax≠i, the
attachment point (that is, the second primary attachment point) is usually a
no-jump attachment point, but can occasionally be a one-jump attachment point
(but not a jumped-over or multiple-jump attachment point). For the c
values less than or equal to 997, there are 1622 primary attachment points where
locmax≠i and 1489 of these are no-jump attachment points and 133 are
one-jump attachment points.
A histogram of the differences between the number of odd
elements in primary one-jump attachment points and the j values
for the c=467 cycles where the (K+L, K) values are (84, 53)
is;

A histogram of the differences between the number of odd elements in primary
one-jump attachments points and the j values for the c=311 cycles
where the (K+L, K) values are (19, 12) is;

As expected, the shoulders on the peak for the c=311 cycles are broader
than those on the peak for the c=467 cycles (taking into account the different numbers
of primary one-jump attachment points). When j is greater than the
number of odd elements in the jump, locmin is usually not equal to u.
An empirical result is;
(44) When j equals the number of odd elements in a
primary one-jump attachment point, locmin equals u.
When locmin doesn't equal u, the difference between the number of odd elements in the
jump and the j value ranges from -11 to 10 for the c values less
than or equal to 997. The corresponding numbers of attachment points are
1, 0, 0, 1, 2, 8, 15, 7, 30, 69, 113, 0, 25, 118, 89, 45, 18, 8, 2, 2, 3, and 1.
The corresponding numbers of attachment points where locmin
can't be reached by successive hops away from u are 0, 0, 0, 0, 0, 1, 0, 0, 4,
5, 6, 0, 25, 12, 11, 5, 2, 0, 0, 0, 1, and 0. Note that these attachment
points account for all of the attachment points where j+1 equals the
number of odd elements in the jump and that most of these attachment points occur
when j is less than the number of odd elements in the jump.
A histogram of the number of odd elements in the jump minus the j
value for the primary one-jump attachment points where locmin doesn't
equal u and locmin can't be reached by successive hops away from
u for the c values less than or equal to 3997 is;

This distribution has a mean of 1.056657 and a standard deviation of
2.295541. A histogram of the number of odd elements in the jump minus the
j value for the primary one-jump attachment points where locmin
doesn't equal u but locmin can be reached by successive hops away
from u for the c values less than or equal to 3997 is;

This distribution has a mean of .6050493 and a standard deviation of
2.969974. When j is greater than the number of odd elements in the
jump, locmax is usually not equal to the last odd element before the
attachment point. An empirical result is;
(45) When j equals the number of
odd elements in a primary one-jump attachment point, locmax equals
the last odd element before the attachment point.
When locmax
doesn't equal the last odd element before the attachment point, the
difference between the number of
odd elements in the jump and the j value ranges from -6 to 2
for the c values less than or equal to 997. The corresponding numbers of
attachment points are 1, 5, 0, 5, 10, 24, 0, 87, and 1. For the c=467
cycles where (K+L, K) equals (84, 53), the difference between the
number of odd elements in the jump (1) and the j value ranges from -4 to
0. The corresponding numbers of attachment points are 1, 4, 7, 6, and 14.
For primary multiple-jump attachment points, locmin equals u and locmax
equals the last odd element before the attachment point. For the c
values less than or equal to 997, the numbers of primary multiple-jump
attachments points where j equals 1, 2, 3, ..., 7 are 556, 447, 82, 9, 1,
1, and 0 respectively (there are 1096 primary multiple-jump attachment points).
The proportions don't change much for different c upper bounds; a table
of proportions where n denotes the number of primary multiple-jump
attachment points is;
cmax= 49999 99997 149999 199999
j=1 5.018008e-001 5.008240e-001 5.004788e-001 5.004156e-001
2 4.099361e-001 4.108239e-001 4.110778e-001 4.110728e-001
3 7.693787e-002 7.689667e-002 7.703393e-002 7.706442e-002
4 9.129327e-003 9.315844e-003 9.303581e-003 9.330295e-003
5 1.855497e-003 1.810723e-003 1.794086e-003 1.802707e-003
6 2.786773e-004 2.807546e-004 2.665826e-004 2.699150e-004
7 5.467719e-005 4.341567e-005 3.855657e-005 3.664347e-005
8 7.055122e-006 3.473253e-006 5.723242e-006 6.233167e-006
9 0.000000e+000 1.157751e-006 9.036697e-007 1.133303e-006
10 0.000000e+000 0.000000e+000 0.000000e+000 1.888838e-007
11 0.000000e+000 0.000000e+000 0.000000e+000 0.000000e+000
n= 566964 1727487 3319797 5294259
For a primary
no-jump attachment point, the probability that j equals 1 is about 1/2,
the probability that j equals 2 is about 1/4, the probability that j
equals 3 is about 1/8, etc. For the c values less than or equal to
997, the numbers of primary no-jump attachment points where j equals 1,
2, 3, ..., 12 are 1265, 627, 302, 152, 83, 37, 18, 18, 3, 1, 2, and 0
respectively. For the c values less than or equal to 199999, the
numbers of primary no-jump attachment points where j equals 1, 2, 3, ...,
21 are 6008288, 2998990, 1505485, 750484, 377569, 188532, 94326, 46823, 23613,
11593, 5914, 3000, 1368, 729, 423, 230, 68, 21, 2, 2, and 0 respectively (there
are 12017460 primary no-jump attachment points).
The Largest Power of 2 That Divides the Difference Between a u Value
and Its Proxy and the Generalized Continued-Fraction Convergents of
log(3)/log(2)
A histogram of j minus the number of jumps from t to the odd
integer before the primary attachment point plus the number of hops between u
and the primary attachment point minus the number of even elements after the
even element before the primary attachment point for the 22851 primary
attachment points for the c values less than or equal to 1999 is;

j and the number of even elements after the even element before a primary
attachment point are complementary variables.
A histogram of j minus the number of even elements after the even element
before the primary attachment point for the 22851 primary attachments points for
the c values less than or equal to 1999 is;

A histogram of j minus the number of even elements after the even
element before the primary attachment point for the 36112285 primary attachment
points for the c values less than or equal to 199999 is;

This distribution has a mean of -0.7955 and a standard deviation of 2.0347.
For cmax=9997, 1999, 2999, ..., 199999, the standard
deviations of the distributions are 2.0402, 2.0386, 2.0378, 2.0377, 2.0359,
2.0356, 2.0346, 2.0348, 2.0349, 2.0346, 2.0348, 2.0347, 2.0346, 2.0346, 2.0347,
2.0345, 2.0346, 2.0345, 2.0346, and 2.0347 respectively. The means of the
distributions are approximately equal to -0.8. The distribution doesn't
change much for different c upper bounds.
For c values less than or equal to 499, this distribution has a mean
of -0.5522 and a standard deviation of 2.0706 (there are 3200 primary
attachment points). For c=467 (and (K+L, K)=(84, 53)), the distribution has a mean of
0.1892 and a standard deviation of 2.1805 (there are 111 primary attachment
points). Since there are no jumped-over attachment points, the differences between the j values and the
numbers of even elements after the even element before the primary
attachment point are skewed to the positive side. (The
differences range from -3 to 9 and the histogram values are 1, 15, 39, 21, 15,
8, 4, 1, 3, 1, 0, 2, and 1 respectively.) Apparently, there is a limit to
how skewed the distribution can be for a given c value. For c=107,
there is apparently only one cycle and the (K+L, K) value is (106,
53). Since the number of even and odd elements in the cycle are the same,
the differences between the j values and the numbers of even elements
after the even element before the primary attachment point are skewed to the
negative side. The distribution has a mean of -1.4 and a standard
deviation of 3.0984 (there are 10 primary attachment points). (The
differences range from -9 to 2 and the histogram values are 1, 0, 0, 0, 0, 0, 1,
2, 2, 1, 2, and 1 respectively.) In cycles having the same number of even
and odd elements and where the number of odd elements equals the denominator of
a generalized continued-fraction convergent of log(3)/log(2), j minus the
number of even elements after the even element before the primary attachment
point is no more
negative (approximately) than the difference for cycles having the (K+L,
K) value of a generalized continued-fraction convergent of log(3)/log(2) is
positive (an empirical result).
A histogram of the sum of the j values minus the sum of the number of
even elements after the even element before the primary attachment point for the
3213 cycles with attachment points for the c values less than or
equal to 1999 is;

This distribution has a mean of -5.2770 and a standard deviation of 8.9742.
The difference between the sum of the j values and the sum of the numbers
of even elements after the even element before the primary attachment point
is likely
to be the most negative in cycles having more even elements than odd elements. The largest difference appears to very slowly increase as c increases.
A quadratic least-squares fit of the means of the distributions plotted against
(cmax+1)/1000 or (cmax+3)/1000 for cmax=9997,
19999, 29999, ..., 199999 is;

(The coefficients are poorly conditioned when the means are plotted against cmax.)
p1=0.0561 with a 95% confidence interval of (0.04223,
0.06996), p2=-2.778 with a 95% confidence interval of (-3.078,
-2.478), and p3=-9.464 with a 95% confidence interval of
(-10.83, -8.097). SSE=12.89, R-square=0.9927, adjusted R-square=0.9919,
and RMSE=0.8709.
A histogram of j minus the number of even elements after the even element
before the primary attachment point where the (K+L, K) value of
the cycle equals a generalized continued-fraction convergent of log(3)/log(2)
for the c values less than or equal to 9997 is;

This distribution has a mean of 0.03171 and a standard deviation of 2.0258
(there are 9462 samples). A
histogram of the sum of the j values minus the sum of the numbers of even
elements after the even element before the primary attachment point where the (K+L,
K) value of the cycle equals a generalized continued-fraction convergent
of log(3)/log(2) for the c values less than or equal to 9997 is;

This distribution has a mean of 0.07266 and a standard deviation of 3.0704
(there are 4129 samples).
A histogram of j minus the number of even elements after the even element
before the primary attachment point where the number of even and odd elements in
the cycle are the same and the K value equals the denominator of a
generalized continued-fraction convergent of log(3)/log(2) for the c
values less than or equal to 9997 is;

This distribution has a mean of -0.6945 and a standard deviation of 1.9292
(there are 2236 samples).
A histogram of the sum of the j values minus the sum of the numbers of
even elements after the even element before the primary attachment point where
the number of even and odd elements in the cycle are the same and the K
value equals the denominator of a generalized continued-fraction convergent of
log(3)/log(2) for the c values less than or equal to 9997 is;

This distribution has a mean of -4.0262 and a standard deviation of 4.8975
(there are 764 samples).
A histogram of the sum of the j values plus d/δ minus the sum
of the numbers of even elements after the even element before the primary
attachment point where the number of even and odd elements in the cycle are the
same and the K value equals the denominator of a generalized
continued-fraction convergent of log(3)/log(2) for the c values less than
or equal to 9997 is;

This distribution has a mean of 1.0524 and a standard deviation of 4.1845
(there are 764 samples). This distribution resembles the corresponding distribution where the (K+L,
K) values equal those of a generalized continued-fraction convergent of
log(3)/log(2). A histogram of these values scaled by 4129/764 (the ratio
of the sample sizes) superimposed
on the corresponding distribution where the (K+L, K) values equal
those of a generalized continued-fraction convergent of log(3)/log(2) is;

For c≤19999, there are 5288 cycles having the (K+L, K)
value of a generalized continued-fraction convergent of log(3)/log(2) and there
are 1903 cycles having an equal number of even and odd elements and a K
value equal to the denominator of a generalized continued-fraction convergent of
log(3)/log(2). The corresponding histograms are;

In general, adding d/δ
"normalizes" values so that they can be compared to those of cycles having
the (K+L, K) values generated by the parity vector p.
The Distribution of [3·log(c)]-a Values
A histogram of [3·log(cmax)]-[3∙log(c)]+a for the 4897 cycles for cmax=2999
superimposed on a chi-square distribution with 6 degrees of freedom is;

This distribution has a mean of 12.1873 and a standard deviation of 10.0945.
[3·log(cmax)]=24, so about 91% of the [3·log(c)]-a values are non-negative. A histogram of
[3·log(cmax)]-[3·log(c)]+a
for the 23132 cycles for cmax=9997 is;

This distribution has a mean of 15.2292 and a standard deviation of 19.0883.
[3·log(cmax)]=27, so about 85% of the [3·log(c)]-a values are non-negative. For cmax equal
to 997, 1999, 2999, ..., and 19999, the means of these distributions are 7.6247,
9.5976, 12.1873, 12.4800, 13.6209, 15.1857, 14.8543, 13.2578, 14.7518, 15.2292,
15.8069, 17.2515, 17.6940, 18.1386, 18.1259, 19.6618, 19.7332, 20.1047, 20.4672,
and 20.9466 respectively and the standard
deviations are 5.6051, 8.5752, 10.0945, 12.1485, 13.3792, 14.7405, 15.9844, 16.5977, 18.0075,
19.0883, 20.1579, 21.1702, 21.8124, 22.9374, 23.5984, 24.4908, 25.1141, 25.8074,
26.3705, and 27.1986 respectively. (The values of [3·log(cmax)]
minus the means are 12.3753, 12.4024, 11.8127, 11.5200, 11.3791, 10.8143,
11.1457, 12.7422, 12.2482, 11.7708, 11.1931, 10.7485, 10.3060, 9.8614, 9.8741,
9.3382, 9.2667, 8.8953, 8.5328, and 8.0534 respectively.)
The distributions resemble a chi-square probability distribution (or an exponential probability distribution), but since
the means and standard deviations increase, the probability that [3·log(c)]-a
takes on a specific value is not fixed. For example, proportions of some
[3·log(c)]-a values (denoted by i) for the
different distributions are;
cmax= 997 1999
2999 3997 4999 5999
6997 7999 8999 9997
i=0 .0045 .0056
.0078 .0081 .0082 .0086 .0080
.0070 .0072 .0072
1 .0071 .0084
.0102 .0113 .0102 .0101 .0096
.0082 .0083 .0083
2 .0109 .0115
.0127 .0127 .0120 .0113 .0106
.0085 .0083 .0081
3 .0084 .0100
.0098 .0102 .0113 .0118 .0108
.0089 .0089 .0091
4 .0161 .0153
.0159 .0143 .0133 .0131 .0122
.0101 .0098 .0095
5 .0141 .0140
.0153 .0146 .0147 .0144 .0135
.0112 .0114 .0114
6 .0206 .0174
.0169 .0169 .0158 .0151 .0140
.0117 .0117 .0117
7 .0308 .0240
.0216 .0184 .0168 .0168 .0151
.0127 .0122 .0124
8 .0219 .0215
.0196 .0177 .0186 .0179 .0166
.0133 .0129 .0131
9 .0379 .0321
.0296 .0265 .0239 .0232 .0204
.0166 .0165 .0162
10 .0463 .0352
.0333 .0290 .0259 .0243 .0219
.0177 .0171 .0171
11 .0668 .0464
.0392 .0335 .0312 .0282 .0258
.0209 .0198 .0188
12 .0521 .0445
.0392 .0327 .0304 .0279 .0251
.0201 .0197 .0195
13 .0758 .0542
.0506 .0437 .0396 .0373 .0329
.0262 .0248 .0243
As expected, the proportions for the larger [3·log(c)]-a
values decrease more rapidly than those for the smaller values. The large
number of cycles (2849) for c=7153 doesn't appear to affect the
proportions for cmax=7999 substantially. The cmaxδmax/log(cmax)
values for cmax equal to 997, 1999, 2999, ..., 9997 are
890.3, 2255.4, 3781.3, 5855.0, 7852.8, 10164.9, 12633.0, 14772.9,
17798.1, and 20719.3 respectively and the numbers of cycles are 1556, 3213,
4897, 6796, 8870, 10807, 13477, 18448, 20820, and 22132 respectively (δmax
denotes the standard deviation of the distribution for cmax).
This composite curve indicates that the a values of the cycles for a
given c value should have a distribution resembling that of an exponential probability distribution.
(Also, the exponential distribution applies to the first success in a Poisson
process and the "waiting time" between successes and would explain the
relationship to Poisson probability distributions.) For example, for K+L=16 and K=10,
there are 504 parity vectors that are distinct under rotation. 216-310=6487=13·499
and there are 456 primitive cycles for c=6487 having a (K+L, K)
value of (16, 10) (438 of which have attachment points), 41 primitive
cycles for c=499 having a (K+L, K) value of (16, 10) (39 of
which have attachment points), and 7 primitive cycles for c=13 having a (K+L,
K) value of (8, 5). Note that 504=456+41+7 (since 16 and 10 are not
relatively prime, there are 7 parity vectors consisting of duplicated
sub-vectors). For the 438 c=6487 cycles with attachment points and
a (K+L, K) value of (16, 10), there are 11 [3·log(c)]-a
values equal to 23, 191 [3·log(c)]-a values equal to 24, and
236 [3·log(c)]-a values equal to 25. These counts would
more closely resemble an exponential probability distribution if there were
other c=6487 cycles having different (K+L, K) values. For c=6487, there are cycles having (K+L, K)
values of (16, 10), (32, 20), (48, 30), (64, 40), (80, 50), and (96, 60).
There are 516 cycles and there are 1, 2, 3, 7, 19, 40, 207, and 237 [3·log(c)]-a
values of 18, 19, 20, 21, 22, 23, 24, and 25 respectively. These counts
more closely resemble an exponential probability distribution. The counts for the
individual (L, K) values are;
(L, K)=(6, 10) (12, 20) (18, 30)
(24, 40) (30, 50) (36, 60)
[3·log(c)]-a=18
0 0
0
0 0
1
19 0
0 0
1 1
0
20 0
0 1
2 0
0
21 0
2 5
0 0
0
22 0
12 5
2 0
0
23 11
28 1
0 0
0
24 191
16 0
0 0
0
25 236
1 0
0 0
0
As discussed in the Journal of Integer Sequences article, there are
frequently cycles for a given c value with (L, K) values
that are multiples of other (L, K) values. In this example,
the function of the cycles with (L, K) values that are a multiple
of (6, 10) is apparent; the modal class (or the average of the modal classes if
the distribution is multimodal) of the distributions of [3·log(c)]-a
values for the different (L, K) values (that is, the values in the
columns of the above matrix) decreases linearly (roughly). (In this example, the modal classes
are 25, 23, 21.5, 21, 19, and 18 respectively.)
For c=7153 (equal to |219-312|), there are cycles
having (L, K) values of (7, 12), (14, 24), (21, 36), (28, 48),
(35, 60), (42, 72), (56, 96), (63, 108), (271, 221), (292, 257), (341, 341), and
(362, 377). There are 2849 cycles and there are 1, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 2, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 2, 0, 1, 1, 0, 0, 2, 4, 4, 11, 25, 55, 125, 314, 1333, and
968 [3·log(c)]-a values of -60, -59, -58, ..., 25
respectively. Including these cycles (say for cmax in the
range from 6499 to 7499) doesn't change the smoothness of the composite curve substantially.
There are also frequently associated cycles (defined
and discussed in the Journal of Integer Sequences article) for a given
c value. Let (L1,
K1) denote the number of even and odd elements in the cycles with
the smallest number of even elements. In associated cycles, the (L,
K) values of cycles are in arithmetic progression with an increment of (L1,
K1) and aren't multiples of (L1, K1).
For
example, for c=1843, the (L, K) values of the cycles
(sorted by increasing L values) are (6, 11), (12, 22), (18, 9), (24, 20),
(30, 31), (36, 42), (42, 53), (48, 64), (54, 51), and (90, 117) (the cycles with
(L, K) values of (18, 9), (24,
20), (30, 31), (36, 42), (42, 53), and (48, 64) are the associated cycles).
There are 44 cycles and there are 1, 0, 0, 0, 0, 0, 1, 1, 0, 3, 1, 2, 0, 2, 2,
1, 2, 3, 11, and 14 [3·log(c)]-a values of 1, 2, 3,
..., 21 respectively. The counts for the individual (L, K)
values are;
(L, K)= (6, 11) (12, 22) (18, 9) (24, 20)
(30, 31) (36, 42) (42, 53) (48, 64) (54, 51) (90,
117)
[3·log(c)]-a= 1
0 0
0 0
0 0
0 0
0 1
2 0
0 0
0 0
0 0
0 0
0
3 0
0 0
0 0
0 0
0 0
0
4 0
0 0
0 0
0 0
0 0
0
5 0
0 0
0 0
0 0
0 0
0
6 0
0 0
0 0
0 0
0 0
0
7 0
0 0
0 0
0 0
0 0
0
8 0
0 0
0 0
0 0
0 1
0
9 0
0 0
0 0
0 0
1 0
0
10 0
0 0
0 0
0 0
0 0
0
11 0
0 0
0 0
1 2
0 0
0
12 0
0 0
0 0
0 0
1 0
0
13 0
0 0
0 1
1 0
0 0
0
14 0
0 0
0 0
0 0
0 0
0
15 0
0 0
1 1
0 0
0 0
0
16 0
0 1
1 0
0 0
0 0
0
17 0
0 0
1 0
0 0
0 0
0
18 0
1 0
1 0
0 0
0 0
0
19 0
3 0
0 0
0 0
0 0
0
20 7
3 1
0 0
0 0
0 0
0
21 14
0 0
0 0
0 0
0 0
0
The associated cycles have the same function as the multiples of cycles; the
modal classes of the distributions of [3·log(c)]-a values
decrease linearly (roughly). The modal classes in this example are 21,
19.5, 18, 16.5, 14, 12, 11, 10.5, 8, and 1. Note that there is a big gap
between the modal classes for the cycles having the last two (L, K)
values (which aren't associated
cycles). When the (L, K) values are sorted by increasing
L values, the modal classes almost always decrease. As previously
shown, a Poisson probability distribution models the number of cycles fairly
well if
only one of the interrelated cycles is counted, only one of the associated
cycles is counted, and only one of cycles with (L, K) values that
are a multiple of another (L, K) value is counted.
For c=2425, the (L, K) values of the cycles (sorted by
increasing L values) are (6, 11), (12, 22), (18, 33), (24, 44), (36, 26),
(42, 37), (48, 48), and (54, 59) (the cycles with (L, K) values of
(36, 26), (42, 37), (48, 48), and (54, 59) are the associated cycles).
(Note that the L value of the first associated cycle is frequently a
multiple of L1.) There are 40 cycles and there are 1, 0, 0, 2, 1, 0, 3, 1, 0, 0, 0, 2, 1, 0, 19
and 10 [3·log(c)]-a values of 7, 8, 9, ..., 22
respectively. The counts for the individual (L, K) values are;
(L, K)= (6, 11) (12, 22) (18,
33) (24, 44) (36, 26) (42, 37) (48, 48) (54, 59)
[3·log(c)]-a= 7 0 0
0 0 0 0 0 1
8 0 0
0 0 0 0 0 0
9 0 0
0 0 0 0 0 0
10 0 0
0 0 0 0 0 2
11 0 0
0 0 0 0 1 0
12 0 0
0 0 0 0 0 0
13 0 0
0 0 1 1 1 0
14 0 0
0 0 0 1 0 0
15 0 0
0 0 0 0 0 0
16 0 0
0 0 0 0 0 0
17 0 0
0 0 0 0 0 0
18 0 0
1 1 0 0 0 0
19 0 0
1 0 0 0 0 0
20 0 0
0 0 0 0 0 0
21 18 1
0 0 0 0 0 0
22 10 0
0 0 0 0 0 0
The modal classes are 21, 21, 18.5, 18, 13, 13.5, 12 and 10.
For c=3689, the (L, K) values of the cycles are (6, 12),
(12, 24), (111, 102), (123, 126), and (147, 174) (there are no associated
cycles, but the difference between (111, 102) and (123, 126) is (12, 24)).
There are 15 cycles and there are 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 3, and 7 [3·log(c)]-a
values of -11, -10, -9, ..., 23 respectively. The counts for the
individual (L, K) values are;
(L, K)= (6, 12) (12, 24)
(111, 102) (123, 126) (147, 174)
[3·log(c)]-a=-11 0 0
0 0 1
-10 0 0
0 0 0
-9 0 0
0 0 0
-8 0 0
0 0 0
-7 0 0
0 0 0
-6 0 0
0 1 0
-5 0 0
1 0 0
-4 0 0
0 0 0
-3 0 0
0 0 0
-2 0 0
0 0 0
-1 0 0
1 0 0
0 0 0
0 0 0
1 0 0
0 0 0
2 0 0
0 0 0
3 0
0 0 0 0
4 0
0 0 0 0
5 0
0
0
0
0
6 0
0
0
0
0
7 0
0
0
0
0
8 0
0
0
0
0
9 0
0
0
0
0
10 0
0
0
0
0
11 0
0
0
0
0
12 0
0
0
0
0
13 0
0
0
0
0
14 0
0
0
0
0
15 0
0
0
0
0
16 0
0
0
0
0
17 0
0
0
0
0
18 0
0
0
0
0
19 0
0
0
0
0
20 0
0
0
0
0
21 0
1
0
0
0
22 3
0
0
0
0
23 7
0
0
0
0
In this case, there are two separate populations of (L, K) values,
one where 2K+L-3K is negative and the other
where it is positive
(the same as for c=7153 and other values).
Another Way for 3n+c Cycles to be Interrelated
An
empirical result is;
(46) For a given c value, if there are two 3n+c
cycles having (L, K) values of (L1, K1)
and (L2, K2) where K1=K2
and L1≠L2, then either L1≤K1
and L2≥K2 or L1≥K1
and L2≤K2.
If there are several such pairs of cycles, say K1=K2,
L1≠L2, K3=K4
(K3≠K1), L3≠L4,
and K5=K6 (K5≠K1,
K5≠K3), L5≠L6,
then one of L1-L2, L3-L4,
L5-L6 divides the other differences in L
values.
Of the 23132 3n+c cycles for c less than or equal to 9997,
there are 24 such pairs of cycles (not counting interrelated cycles). Note that for a given c value and number of odd elements, there can be at most three cycles (not
counting interrelated cycles) having different L
values. Belaga14 calls numbers of the form Bk,l
= 2l - 3k > 0 "Collatz numbers" and
gives a rephrasing of the Diophantine interpretation of the Collatz problem:
no non-trivial Collatz number can be a divisor
of numbers from a certain finite set of natural numbers called the "Collatz (k,
l)–corona". A Collatz number such
that 2l-1 - 3k < 0 is called "narrow". When 2K+L-3K is
positive and (K+L, K) is a generalized continued-fraction
convergent of log(3)/log(2), the Collatz number is narrow. In all of the
above 24 pairs of cycles, neither of the corresponding Collatz numbers is narrow. An
empirical result is;
(47) For a given c value, if there are two 3n+c
cycles have (L, K) values of (L1, K1)
and (L2, K2) where L1=L2
and K1≠K2, then either L1≤K1
and L2≥K2 or L1≥K1
and L2≤K2 (usually). If there are
several such pairs of cycles, then one of the differences in K values
divides the other differences in K values (apparently always).
For the 3n+c cycles for c less than or equal to 9997, there
are 107 such pairs of cycles (not counting interrelated cycles). An
exception occurs for a pair of cycles for c=145 having (L, K)
values of (16, 18) and (16, 32) (16 is approximately equal to 18). An
exception occurs for a pair of cycles for c=1009 having (L, K)
values of (56, 37) and (56, 46) (these are the only cycles for this c
value, so conditions are less stringent). A similar exception occurs for a
pair of cycles for c=7063 having (L, K) values of (168,
192) and (168, 174). A third type of exception occurs when there are many
such pairs of cycles for a given c value. For example, when c=6305,
the (L, K) values that can be paired are [(24, 12), (24, 20), (24,
28), (24, 36)], [(48, 40), (48, 48), (48, 56)], and [(72, 60), (72, 68), (72,
84)]. Another empirical result is;
(48) For a given c value, if there are two 3n+c
cycles having (K+L, K) values of (K1+L1,
K1) and (K2+L2, K2)
where K1+L1=K2+L2,
K1≠K2, then either L1≤K1
and L2≥K2 or L1≥K1
and L2≤K2.
If there are several such pairs of cycles, then one of the differences in
K values divides the other differences in K values and one of the
differences in L values divides the other differences in L values.
Note that for a given c value and length, there can be at most three
cycles (not counting interrelated cycles) having different numbers of odd
elements. Of the 23132 3n+c cycles for c less than or
equal to 9997, there are 11 such pairs (not counting interrelated cycles) and in
every case, neither of the corresponding Collatz numbers is narrow. Proposition (48) is
usually valid (with the same kinds of exceptions as for Proposition (47))
for pairs of cycles where fK1+gL1=fK2+gL2
(this would account for there being few cycles that aren't interrelated).
For the 333 c values less than or equal to 997, the number of c
values having 1, 2, 3, 4, 5, 6, 7, and 8 cycles (not counting interrelated
cycles) are 109, 121, 70, 20, 8, 1, 4, and 0 respectively. (As
previously mentioned, the number of interrelated cycles having a given (K+L,
K) value is determined by the number of parity vectors having this length
and number of 1's that are distinct under rotation.) For a given c
value, pairs of cycles that satisfy the equation fK1+gL1=fK2+gL2
(or have equal L values and unequal K values or equal K
values and unequal L values) can also be considered to be
interrelated. For example, when c=9215, the pairs of cycles having
[(L1, K1) (L2, K2)]
values of [(24, 20), (12, 22)], [(18, 9), (6, 11)], [(36, 42), (24, 44)],
[(30, 31), (18, 33)], [(42, 29), (18, 33)], [(42, 29), (30, 31)], [(48, 40),
(24, 44)], [(48, 40), (36, 42)], [(42, 53), (54, 51)], and [(48, 64), (60, 62)]
can be considered to be interrelated. For all combinations of
relatively prime f and g values less than 13 (which usually
accounts for most solutions), the adjusted number of c values having 1,
2, 3, 4, 5, 6, 7, and 8 cycles are 127, 125, 61, 12, 7, 1, 0, and 0 respectively. This
appears to be a Poisson probability distribution where λ is approximately equal
to 1. For the 667 c values less than or equal to 1999, the number
of c values having 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 cycles (not counting
interrelated cycles) are 220, 246, 134, 34, 21, 6, 5, 0, 0, and 1 respectively.
Accounting for the second type of interrelated cycles, the number of c
values having 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 cycles are 247, 254, 121, 25,
15, 5, 0, 0, 0, and 0 respectively. For the 1000 c values less than
or equal to 2999, the number of c values having 1, 2, 3, 4, 5, 6, 7, 8,
9, and 10 cycles (not counting interrelated cycles) are 321, 361, 198, 66, 34,
9, 8, 1, 1, and 1 respectively. Accounting for the second type of
interrelated cycles, the number of c values having 1, 2, 3, 4, 5, 6, 7,
8, 9, and 10 cycles are 359, 368, 188, 54, 23, 6, 2, 0, 0, and 0 respectively.
The mean of this distribution (where x=0, 1, 2, ...) is 1.04.
A difficulty with this approach is determining an upper bound of f and
g. This approach hasn't been thoroughly investigated.
The Order of a 3n+c Cycle
The order of a cycle is defined to be the smallest natural number of the form
3∙2k greater than or equal to the absolute value of every
element of the cycle. In the following, if all the absolute values of the
elements of an extended sequence of a cycle are less than the cycle order, then the
extended sequence is further extended backwards until the cycle order has been
exceeded (the elements of this portion of the extended sequence will be integers
of the form 2it where t is the odd integer divisible by
3). The extension order is then taken to be the cycle
order. If the cycle order has already been exceeded between the odd
integer divisible by 3 and the attachment point, the order of the extension is
defined to be the smallest natural number of the form 3∙2k
greater than or equal to the absolute value of every element of the extended
sequence. The extended sequence is then further extended backwards until
this order has been exceeded. (For the remainder of this article, this
will be referred to as being the extended sequence of an attachment point.) For example, the extended sequence for the
c=1 cycle is {-336, -168, -84, -42, -21, -62, -31, -92, -46, -23, -68,
-34, -17, -50, -25, -74, -37, -110, -55, -164, -82, -41, -122, -61, -182, -91,
-272, -136, -68} and the cycle order and extension order are 384. An
empirical result is;
(49) For a one-jump attachment point, the cycle order equals the extension
order.
Let P denote the primary attachment point having the largest absolute
value. In most 3n+c cycles, 4 times the absolute value of
P determines the orders (all the same) of all the extended sequences of the
cycle. Many exceptions are associated with multiple-jump attachments
points. When there is a multiple-jump to P and there is a secondary
attachment point, the order of the extended sequence of the primary attachment
point may be different from the order of the extended sequence of the secondary
attachment point.
Let m be the number of odd elements in an extended sequence up to the
attachment point (where the element following an odd element i is
temporarily defined to be (3i+c)/2) and e the number of
even elements. For a no-jump attachment point, e is greater than or
equal to m. For a one-jump attachment point where c≤151,
e+1 is greater than or equal to m. For a multiple-jump or
jumped-over attachment point where c≤151 and the absolute value of the odd element immediately
before the attachment point is greater than order/6, e+2 is
greater than or equal to m. Of the 649 attachment points of the
c values less than or equal to 151, e is less than m for only
32 attachment points. The only c values less than or equal to 151
where e is less than m for a one-jump attachment point are 19, 31,
97, 115, and 139. In every case, the attachment point equals P and
4|P| determines the order of the extended sequence. A histogram of
the e-m values for the 1807 one-jump attachment points for c
values less than or equal to 499 is;

As c
increases, the upper bound of m-e appears to gradually increase. For example,
for c=259 and 271, m-e=2 for a one-jump attachment point. In
both cases, the attachment point equals P and 4|P| determines the
order of the extended sequence. A histogram of the e-m values for
the 19223351 one-jump attachment points for cmax=199999
superimposed on a normal probability distribution having the same parameters (a
mean of 8.5393 and a standard deviation of 3.4633) is;
A linear least-squares fit of the means of these distributions plotted against
log((cmax+1)/1000) or log((cmax+3)/1000) for
cmax=997, 1999, 2999, ..., 199999 is;

p1=0.7478 with a 95% confidence interval of (0.7447, 0.7509)
and p2=4.567 with a 95% confidence interval of (4.553, 4.581).
SSE=0.08784, R-square=0.9991, adjusted R-square=0.9991, and RMSE=0.02106.
A cubic least-squares fit of the standard deviations of these distributions
plotted against log((cmax+1)/1000) or log((cmax+3)/1000)
for cmax=997, 1999, 2999, ..., 199999 is;

p1=0.006052 with a 95% confidence interval of (0.005319,
0.006784), p2=-0.07311 with a 95% confidence interval of
(-0.08006, -0.06616), p3=0.3758 with a 95% confidence interval
of (0.3558, 0.3958), and p4=2.628 with a 95% confidence
interval of (2.61, 2.646). SSE=0.02255, R-square=0.9901, adjusted
R-square=0.99, and RMSE=0.01073.
For c=187, m-e=3 for a
multiple-jump attachment point where the absolute value of the odd element immediately before the
attachment point is greater than order/6. In general, m-e is
relatively large for multiple-jump or jumped-over attachment points when there
are associated primary, secondary, tertiary, etc., attachment points.
Let max denote the odd integer in the cycle
having the largest absolute value and let i denote the odd integer immediately before
the
primary attachment point following max ((3i+c)/4 equals the primary attachment
point). For example, for a cycle for c=5, max=3397 and the
sequence between max and the primary attachment point is {3397,
10196, 5098, 2549, 7652, 3826, 1913, 5744, 2872, 1436} (i=1913 and
3397→2549→1913). Empirical results are;
(50) If i≠max and max jumps to i (either by one or
multiple jumps), then the primary attachment point is a no-jump attachment point
and the corresponding t value is less than max.
(51) If i≠max and max jumps over i, then the primary
attachment point is a one-jump attachment point and the corresponding t
value is less than max.
If the primary attachment point is P (that is, i=max) and 4|P|
determines the extension order, then the primary attachment point is usually a
one-jump attachment point (but may be a multiple-jump attachment point or even a
no-jump attachment point).
3n+c Cycles With Only One Attachment Point
In this paragraph, cycles containing only one attachment point are discussed.
Also, the order of the extended sequence is required to have been determined by
4|P|. The sequence vector of such an extended sequence mostly has
bilateral symmetry when the number of 2's in the sequence vector (not counting
the last element of the sequence vector) is even (usually, it is necessary to
disregard the first and last elements of the sequence vector when considering
the symmetry, but sometimes it is also necessary to disregard the second or
next-to-last elements of the sequence vector). Since there is only one
attachment point, the sequence vector in the interior of the cycle is a 1-2
sequence vector. Then the sequence vector of the extended sequence is a
1-2 sequence vector except for the first and last elements of the sequence
vector. (The first element of the sequence vector does not indicate that
there is an odd sequence element immediately before the extended sequence; it
just counts the number of even sequence elements before the first odd sequence
element. A similar situation applies for the last element of the sequence
vector.) The sequence vectors of the extended sequences of the
interrelated cycles for c=13 are (4, 1, 1, 1, 1, 2, 2), (3, 2, 1, 1, 1,
2, 1, 2), (4, 1, 2, 1, 1, 2, 1, 1, 2), (4, 1, 1, 2, 1, 2, 1, 1, 1, 2), and (5,
1, 1, 1, 2, 2, 1, 1, 1, 1, 2). The sequence vectors of the extended
sequences of the interrelated cycles for c=37 and a cycle length of 9 are
(6, 2, 1, 2, 1, 2) and (5, 1, 2, 2, 1, 1, 2). The sequence vectors of the
extended sequences of the interrelated cycles for c=47 and a cycle length
of 11 are (4, 1, 1, 1, 2, 2, ), (4, 2, 1, 1, 2, 1, 2), (6, 1, 2, 1, 2, 1, 1, 2),
and (7, 1, 1, 2, 2, 1, 1, 1, 2). The sequence vectors of the extended
sequences of the interrelated cycles for c=101 and a cycle length of 10
are (6, 2, 1, 2, 2) and (5, 1, 2, 2, 2). In all of these cases, it is
possible to list the interrelated cycles so that the number of 1's between the
pair of 2's (if there is a pair) decreases by one and the extension order remains
the same or increases for each successive interrelated cycle.
Generalized Dead Limbs
Consider a 3n+1 sequence where the fourth-to-last element of the sequence
(denoted by i) is odd, the third-to-last element of the sequence is
divisible by 8, and the sequence has been extended backwards (without any
restrictions on the path taken), until an odd integer divisible by 3 has been
encountered. The order of this sequence is defined to be the smallest
natural number of the form 3∙2k greater than or equal to the
element in the sequence with the largest absolute value. The sequence is
then further extended backwards until the order is exceeded. Note that if
the absolute value of i is greater than the order divided by 6, then the
absolute value of the third-to-last element of the sequence (3i+1) is
greater than the order divided by 2, that is, the third-to-last element of the
sequence (along with other elements of the sequence) determines the order.
When the absolute value of i is greater than the order divided by 6,
these sequences will be referred to as "generalized dead limbs" (ordinary dead
limbs will be defined later).
In the following, the element after an odd element j
is temporarily defined to be (3j+1)/2 (for the purpose of determining
lengths). Let e denote the number of even elements in a generalized
dead limb, m the number of odd elements, and l the number of
elements. Also, generalized dead limbs containing duplicated cycles
are excluded. An empirical result is;
(52) For a given number of odd elements in a generalized dead limb, the
number of even elements is mostly fixed; the number of even elements can deviate
by at most 1.
For example, for m=1, e can equal 4 or 3. (The (e,
m) value will be denoted by ((4, 3), 1).) (e, m)
values for generalized dead limbs are ((4, 3), 1), ((5, 4), 2), ((5, 4), 3),
((6, 5), 4), ((6, 5), 5), ((7, 6), 6), ((8, 7), 7), ((8, 7), 8), ((9, 8), 9),
((9, 8), 10), ((10, 9), 11), ((11, 10), 12), ((11, 10), 13), ((12, 11), 14),
((12, 11), 15), ((13, 12), 16), ((13, 12), 17), ((14, 13), 18), ((15, 14), 19),
((15, 14), 20), ((16, 15), 21), (16, 15), 22), ((17, 16), 23), ((18, 17), 24),
.... An empirical result is;
(53) The adjusted (l, m) values (where l is
decremented by 4 or 3) of generalized dead limbs include the generalized
continued-fraction convergents of log(3)/log(2).
The (l, m)
value of a 3n+1 cycle is a generalized continued-fraction convergent of
log(3)/log(2) (based on empirical evidence). (Assuming the factor of
1.000001 in Simons and de Weger's inequality can be reduced to 1.0, the (l,
m) value of a 3n+1 cycle [n>0] is a continued-fraction convergent of
log(3)/log(2).) For example, the (l, m) value of the 3n+1
cycle {-34, -17, -25, ..., -68} is (11, 7) and the (l, m) value of
the extended sequence {-336, -168, -84, ..., -68} (a generalized dead limb
containing the cycle) is
(19, 10). An empirical result is;
(54) The (l, m) value of a generalized dead limb minus the (l,
m) value of a generalized continued-fraction convergent of log(3)/log(2)
is the (l, m) value of a shorter generalized dead limb.
Let f denote the mapping of the number of odd elements in a generalized
dead limb to the smaller of the two possible numbers of even elements in the
limb. Attachment points were previously defined for cycles. The
definition of attachment points for generalized dead limbs is the same; the
attachment points are just not necessarily in cycles. An empirical result
is;
(55) The number of even elements in a generalized dead limb containing
x primary attachment points is optimal in that the number of even elements
up to the yth primary attachment point, y<x, is greater than or
equal to f(m) where m is the number of odd elements up to
the yth primary attachment point.
Weibull probability distributions are used to model birth and decay processes
and have a scaling and shaping parameter.
For the generalized dead limbs where the odd elements divisible by 3 are less
than a fixed amount and the orders are less than a fixed amount, the number of
even elements (for a given number of odd elements) up to the yth primary
attachment point has a Weibull probability distribution. For example, for generalized
dead limbs (in the 3n-1 sequence, n>0) where the odd
elements divisible by 3 are less than or equal to 99999999, x=5, and y=3, the numbers of generalized dead
limbs where m=10 and e-8 equals 0, 1, 2, ..., 19 are 62, 1246,
2939, 3626, 3213, 2097, 1307, 651, 338, 168, 99, 51, 15, 8, 0, 0, 1, 1, 0, and 1 respectively (f(10)=8).
The parameters of the Weibull probability distribution for this data
(excluding the 62 values equal to 0) are 4.2974 (with a 95% confidence interval of (4.2640,
4.3310) and 2.1167 (with a
95% confidence interval of (2.0921, 2.1415). A Weibull plot of the data is;

A histogram of the data and the corresponding Weibull probability
distribution is;

A plot of the Weibull scaling parameters for m=3, 4, 5, ..., 20 and
where the odd elements divisible by 3 are less than or equal to 99999999 is;

The curve of smaller values is for when the odd elements divisible by 3 are
less than or equal to 999999999. The scaling parameters don't change much
for this larger sample size.
A plot of the Weibull shaping parameters for m=3, 4, 5, ..., 20 and
where the odd elements divisible by 3 are less than or equal to 99999999
is;

The curve of smaller values is for when the odd elements divisible by 3 are
less than or equal to 999999999. The shaping parameters don't change much
for this larger sample size.
When c>1, the behavior of such sequences approaches that of c=1
in a limiting sense, that is, for a fixed c value and a sufficiently
large order, the sequences have the same (l, m) values as for
c=1 (an empirical result).
For the 3n+1 cycle and the extended sequence of P (-68), (8, 3)
((19, 10) [the (l, m) value of the extended sequence] minus (11,
7) [the (l, m) value of the cycle and a generalized
continued-fraction convergent of log(3)/log(2)]) is the (l, m)
value of a shorter generalized dead limb. Similar cycles occur in general
3n+c sequences. For the 3n+5 cycle and the extended
sequence of P where P=1562, (5, 1) ((32, 18) [the (l, m)
value of the extended sequence] minus (27, 17) [the (l, m) value
of the cycle and a generalized continued-fraction convergent of log(3)/log(2)])
is the (l, m) value of a shorter generalized dead limb. For
another 3n+5 cycle and extended sequence having (l, m)
values of (27, 17) and (32, 18) respectively, the difference is (5, 1).
For the 3n+13 cycle and the extended sequence of P where P=454,
(5, 1) ((13, 6) [the (l, m) value of the extended sequence] minus
(8, 5) [the (l, m) value of the cycle and a continued-fraction
convergent of log(3)/log(2)]) is the (l, m) value of a shorter
generalized dead limb. For four other 3n+13 cycles having (l,
m) values of (8, 5), the differences are (6, 2), (8, 3), (9, 4), and (11,
5) (all (l, m) values of shorter generalized dead limbs).
For the 3n+13 cycle and the extended sequence of P where P=1048,
(5, 1) ((29, 16) [the (l, m) value of the extended sequence] minus
(24, 15) [the (l, m) value of the cycle and a generalized
continued-fraction convergent of log(3)/log(2)]) is the (l, m)
value of a shorter generalized dead limb. For the 3n+23 cycle and
the extended sequence of P where P=-23704, (12, 6) ((31, 18) [the
(l, m) value of the extended sequence] minus (19, 12) [the (l,
m) value of the cycle and a generalized continued-fraction convergent of
log(3)/log(2)]) is the (l, m) value of a shorter generalized dead
limb. For six other 3n+23 cycles having (l, m) values
of (19, 12), the differences are (12, 6), (8, 3), (9, 4), (5, 1), (7, 2), and
(5, 1) (all (l, m) values of shorter generalized dead limbs).
For two of these cycles, 4|P| does not determine the order of the
extended sequence (this frequently occurs for interrelated cycles).
For the 3n+29 cycle containing the primary attachment points 788552,
194366, 79082, 73934, 41606, and 18794, (7,2) ((72, 43) minus (65, 41) [a
continued-fraction convergent of log(3)/log(2)]) is the (l, m)
value of a shorter generalized dead limb. For the 3n+29 cycle
containing the primary attachment points 1707830, 1441016, 360254, 577232,
36902, 20306, and 7622, (10, 4) ((75, 45) minus (65, 41)) is the (l, m)
value of a shorter generalized dead limb. For the 3n+71 cycle
containing the primary attachment points 41360 and 17042, (6, 2) ((33, 19) minus
(27, 17)) is the (l, m) value of a shorter generalized dead limb.
For four other 3n+71 cycles having (l, m) values of (27,
17), the differences are (6, 2), (5, 1), (5, 1), and (5, 1) (all (l, m)
values of shorter generalized dead limbs). For two of these cycles, 4|P|
does not determine the order of the extended sequence. For the 3n+139 cycle containing the primary
attachment point 16472, (20, 11) ((31, 18) minus (11, 7)) is the (l, m)
value of a shorter generalized dead limb. For twenty-three other 3n+139
cycles having (l, m) values of (11, 7), the differences are (13,
6), (13, 7), (10, 5), (9, 4), (11, 5), (12, 6), (6, 2), (9, 4), (5, 1), (8, 3),
(9, 4), (6, 2), (11, 5), (5, 1), (8, 3), (7, 2), (8, 3), (5, 1), (6, 2), (5, 1),
(7, 2), (5, 1), and (5, 1). Except for (13, 7), these differences are (l,
m) values of shorter generalized dead limbs. (The permissible (l,
m) values for a generalized dead limb containing seven odd elements are (15,
7) and (14, 7).) For five of these cycles, 4|P| does not determine
the order of the extended sequence. Similar 3n+c cycles and extended sequences occur for c=311, 343,
355, 467, ....
Hypothetical 3n+1 Cycles
Properties of 3n+1 cycles can be inferred from those of general 3n+c
cycles that are in generalized dead limbs and have (l, m) values
of generalized continued-fraction convergents of log(3)/log(2). That a 3n+1
cycle having an attachment point should be in a generalized dead limb is to be
expected since most 3n+c cycles having attachment points are in
generalized dead limbs and the 3n+1 sequence is comparatively
"well-behaved". Catalan's conjecture (proved by Mihăilescu15)
states that the only natural number solutions of xa-yb=1
are x=3, a=2, y=2, and b=3. The only solution
of 2l-3m=-1 is then (3, 2). Also, |2l-3m|
increases monotonically (apparently) for (l, m) values that are
generalized continued-fraction convergents of log(3)/log(2) (excluding (2, 1),
(4, 2), (6, 4), and (9, 6)), so there shouldn't be any more 3n+1 cycles
where |2l-3m|=1. Study of 3n+c
cycles where c properly divides |2l-3m| and the (l, m) values are relatively large should yield expected
properties of any other 3n+1 cycles (the number of odd elements in a hypothetical
3n+1 cycle [n>0] has been confirmed to be very large). A c value
of 467 (and several others) fulfills these and the above requirements.
When c=467, there are fifteen primitive cycles having (l, m)
values of (84, 53) (a continued-fraction convergent of log(3)/log(2)) and these
cycles have 120 attachment points. Empirical results are;
(56) When the domain of the absolute values of the u values and the
absolute values of their proxies is
sufficiently small, the (l, m) value of a 3n+c cycle
is a generalized continued-fraction convergent of log(3)/log(2), the cycle is in
a generalized dead limb, and the (l, m) value of the extended
sequence of P
minus the (l, m) value of the cycle is the (l, m)
value of a shorter generalized dead limb.
(57) When the domain of the absolute values of the u
values and the absolute values of their proxies is sufficiently small, all the extended sequences of a 3n+c cycle have the
same order, the sign does not change in an extended sequence, and there are more even
elements in an extended sequence than odd elements (the only possible (e,
m) values of the extended sequence of P are then ((4, 3), 1), ((5,
4), 2), ((5, 4), 3), ((6, 5), 4), ((6, 5), 5), ((7, 6), 6), ((8, 7), 7), ((8,
7), 8), and ((9, 8), 9)).
(58) When the domain of the absolute values of the u
values and the absolute values of their proxies is sufficiently small, there are no jumped-over attachment points (so
that the attachment points are either primary or secondary attachment points),
P is a one-jump attachment point, one-jump or multiple-jump attachment
points are primary attachment points, secondary attachment points are no-jump
attachment points, multiple-jump attachment points do not have associated
secondary attachment points, and a multiple-jump attachment point is preceded
by a no-jump attachment point (possibly a primary attachment point).
Here, "sufficiently small" means being on the verge of becoming too small. For a c=467 cycle, the
plot of the |u| values and the absolute values of the corresponding proxy
values versus their domain is;

(The x values have been scaled up by a factor of 108 and all
but three data points are shown. No shape-preserving interpolation of data
points is done.) The domain is (-2.390748e-007,
4.432486e-007).
As shown previously, the number of even elements in the extended sequence is
sometimes smaller than the number of odd elements for a one-jump
attachment point (especially when the attachment point is P). For
two of the cycles for c=467, the number of even elements in an extended
sequence is one less than the number of odd elements and this occurs for
one-jump attachment points where the attachment point is P. For four of the 71 one-jump attachment
points for the c=467 cycles, t≡u(mod 2j)
where j is greater than the number of odd elements in the jump (in every
case, locmin is not equal to u). For three of the 15 cycles,
there is not a one-jump attachment point where j equals the number of odd
elements in the jump.
When c=311, there are two primitive cycles having an (l, m)
value of (57, 36) (a generalized continued-fraction convergent of log(3)/log(2)).
There are 11 attachment points and these attachment points have the same properties as the c=467
cycles. For one of the cycles, the number of even elements in an extended
sequence equals the number of odd elements and this occurs for a one-jump
attachment point where the attachment point is P. For one of these
cycles, there is not a one-jump attachment point where j equals the
number of odd elements in the jump. When c=311,
there are seventeen primitive cycles having an (l, m) value of
(38, 24) (a generalized continued-fraction convergent of log(3)/log(2)).
There are 66 attachment points and these attachment points have the same properties as the c=467
cycles except that there are two jumped-over attachment points (in different
cycles). For two of the cycles the number of even elements in an extended
sequence is one less than the number of odd elements and this occurs for
one-jump attachment points where the attachment point is P. For
fourteen of the 41 one-jump attachment points, t≡u(mod 2j)
where j is greater than the number of odd elements in the jump (usually
locmin is not equal to u). For seven of the cycles,
there is not a one-jump attachment point where j equals the number of odd
elements in the jump. The
domains of the absolute values of the u values and the absolute values of
their proxies are somewhat larger than
the domains of the c=467 cycles having (l, m) values of
(84, 53).
When c=343, there is a primitive cycle having an (l, m)
value of (149, 94) (a generalized continued-fraction convergent of
log(3)/log(2)). The domain of the absolute values of the u values
and the absolute values of their proxies
is (-6.216047e-007, 1.015725e-006), somewhat larger than the domains of the c=467
cycles having (l, m) values of (84, 53). There are 15
attachment points and these attachment points have the same properties as the c=467 cycles
having (l, m) values of (84, 53) except
that P is a no-jump attachment point. For all eight one-jump
attachment points, t≡u(mod 2j) where j is
less than or equal to the number of odd elements in the jump. For three of
these attachment points, j equals the number of odd elements in the jump.
When c=1091, there is a primitive cycle having an (l, m)
value of (130, 82) (a generalized continued-fraction convergent of
log(3)/log(2)). The domain of the absolute values of the u values
and the absolute values of their proxies
is (-3.446479e-007, 8.889605e-007), somewhat larger than the domains of the c=467
cycles having (l, m) values of (84, 53). There are 12
attachment points and these attachment points have essentially the same properties as the c=467
cycles having (l, m) values of (84, 53) except that there is a jumped-over attachment point and the number of
even elements in an extended sequence for a multiple-jump attachment point is
equal to the number of odd elements. For one of the 7 one-jump attachment points, t≡u(mod 2j)
where j is greater than the number of odd elements in the jump (locmin
is not equal to u). For two of these attachment points,
j equals the number of odd elements in the jump.
When c=2507, there are three primitive cycles having an (l,
m) value of (76, 48) (a generalized continued-fraction convergent of
log(3)/log(2)) and the domains of the absolute values of the u values
and the absolute values of their proxies
are (-1.018299e-006, 2.239814e-006), (-2.209624e-007, 7.065484e-007), and
(-1.465981e-006, 2.967221e-006). In one of the cycles, P is a
no-jump attachment point. In another cycle, there is a jumped-over
attachment point and the number of even elements in an extended sequence for a
one-jump attachment point (that of P) is equal to the number of
odd elements. In the remaining cycle, there is a jumped-over attachment
point preceding a multiple-jump attachment point. For one of the 11 one-jump
attachment points for these cycles, t≡u(mod 2j) where
j is greater than the number of odd elements in the jump (locmin is
not equal to u). For one of these cycles, j equals the
number of odd elements in the jump for three of the 5 one-jump attachment
points. Although the domains
appear to be small, they are not small enough for this large of a c value
to exhibit all of the above properties; many anomalies occur.
For comparison, when c=29, there are two primitive cycles having an (l,
m) value of (65, 41) (a continued-fraction convergent of log(3)/log(2)) and
the domains of the absolute values of the u values and the absolute
values of their proxies are (-1.136015e-005,
2.425506e-005) and (-2.555711e-005, 3.583320e-005). There are 15
attachment points and these attachment points have the same properties as the c=467 cycles having (l,
m) values of (84, 53) (except there are no anomalies).
When c=5, 13, 23, 71, 139, and 355,
there are cycles having (l, m) values of generalized
continued-fraction convergents of log(3)/log(2) that also have some properties of the
c=467 cycles having (l, m) values of (84, 53) .
Also, when c=407, cycles having an (l, m) value of (44, 28)
(almost equal to (46, 29) [a generalized continued-fraction convergent of
log(3)/log(2)]) have some properties of the c=467 cycles.
This is currently the extent to which 3n+c cycles with attachment
points have been investigated. In the remainder of the article, 3n+c
cycles not having attachment points are discussed.
Least-Residue Trees
In this section and the remaining sections, the original definition of 3n+c sequences
(where n>0 and c≥-1) is used. Consider the
following "least-residue" tree (where "{}" denotes a limb) consisting of the
natural numbers less than 3∙2k,
k=4;
{4, 2, 1}
{24, 12, 6, 3, 10, 5, 16, 8}
{36, 18, 9, 28, 14, 7, 22, 11, 34, 17}
{30, 15, 46, 23}
{26, 13, 40, 20}
{38, 19}
{42, 21}
{32}
{44}
{25}
{27}
{29}
{31}
{33}
{35}
{37}
{39}
{41}
{43}
{45}
{47}
Each limb consists of a snippet from the 3n+c sequence (in this case,
c=1).
Note that "odd" paths are taken at nodes when tracing back through the
sub-sequences (that is, if i is an even element of the sub-sequence and 3 divides
i-c, then the element prior to i is (i-c)/3). A limb containing an odd
natural number that is divisible by 3 will be referred to as a "dead" limb
(and limbs that aren't dead will be referred to as being "alive"). A limb ending in an odd natural number greater than 2k
attaches to
the beginning of another limb (or possibly itself) when going from one size of
the tree to the next. That is, if i is the last natural number in the
limb, then 3i+c "cements" the limb ending in i to the beginning of another limb
to form a longer limb in the next larger least-residue tree. A
dead limb that starts with an even natural number and ends with an odd natural
number cannot attach to itself at its beginning (or any point up to and
including the odd natural number divisible by 3) since (3i+c)/2
(where i is the last natural number in the limb) is not divisible by 3.
Similarly, a limb ending in an odd natural number greater than 2k
cannot attach to the interior of another limb (or itself) since the even natural
numbers in the interior of a limb (and, if the limb is dead, to the right of the odd natural number
divisible by 3) are either of the form 3j+c where j is a natural number or are less than
half the order, and the odd natural numbers in the interior of a limb are less
than half the order. (These limbs have properties similar to those of
interrelated 3n+c cycles having 1-2 sequence vectors. Also,
as will be shown, there is a connection between these limbs and "admissible"
parity vectors and Terras' stopping time.)
Note that there is no overall "gain" in a cycle. The feature of
least-residue trees that makes them relevant to cycle formation is that there is
no gain (at least in principle) from the end of a limb ending in an odd natural
number greater than 2k to the beginning of the limb, that is,
the last element of the limb is greater than order/3 and the first
element of the limb is greater than order/2 (unproven as yet).
Also, note that the definition of least-residue trees (where "odd" paths are
taken) is not broad enough to encompass all possible 3n+c cycle
formation. (All cycles will appear in the dead limbs of a least-residue
tree of sufficiently large order, however, active limb formation is easier to
analyze. More general least-residue trees will be introduced later.)
Another feature of least-residue trees is that they provide a means to define
"trivial" cycles. (What trivial cycles are is intuitively obvious, but
they haven't been defined.) The 3n-1 cycles of {2, 1} and {20, 10,
5, 14, 7} will be classified as trivial cycles (the other known 3n-1
cycle contains an element divisible by 8, so this paves the way for a unified
treatment of the 3n+1 and 3n-1 cycles). The objective in the
following (not attained) is to use mathematical induction to prove the existence
of a 3n+c "process". (In this process, a limb ending in an
odd natural number greater than 2k cannot attach to itself at
its beginning [apparently] when c=1 or -1. For a sufficiently large
k, an "odd" path is in a limb of a least-residue tree [assuming that
there is a jump in the "odd" path ending in an even natural number and that
there is a backward jump in the "odd" path ending in an odd natural number
divisible by 3]. By default, there would not be any cycles for 3n+1
or 3n-1 sequences having 1-2 sequence vectors.) A limb ending in an
odd natural number greater than 2k must attach to the
beginning of some limb when going to the next larger size of the tree; remaining
questions are how many limbs end in an odd natural number greater than 2k
and which limbs they attach to. When c>1, there are sometimes limbs in the least-residue trees starting with an
even natural number and ending in an odd natural number i where 3i+c>3∙2k
and i<2k (this cannot occur for c=1 or -1,
one of the unique properties of the 3n+1 and 3n-1 sequences).
In the following, this is not considered to be a different kind of limb since
the properties of these limbs haven't been fully determined yet. Nine different
kinds of limbs are required to define the 3n+c process (this is an
empirical result).
For convenience, the following sets will be defined for
c=1 (when c≠1,
certain sets are permuted). Let E denote the set of limbs that are not
dead, have more than one element, and end in an even natural number. Let
F denote the set of limbs that are dead and end in an even natural number.
(Limbs in E or F are already attached to other limbs.)
Let G denote the set of limbs that end in an odd natural number less than 2k
(other than the previously mentioned limbs for c>1, these limbs always contain
cycles [this is an empirical result]).
Let A denote the set of limbs ending in an element of {2k+1, 2k+9,
2k+17, ..., 2k+1-7}, let B denote the set of limbs ending
in an element of {2k+3, 2k+11, 2k+19, ..., 2k+1-5},
let C denote the set of limbs ending in an element of {2k+5, 2k+13,
2k+21, ..., 2k+1-3}, and let D denote the set of limbs
ending in an element of {2k+7, 2k+15, 2k+23,
..., 2k+1-1}. (When c≡1(mod 8), the sets A,
B, C, and D are not
permuted. When c≡3(mod 8), the sets B, A, D, and
C become the sets A, B,
C, and D respectively. When c≡5(mod 8), the sets C,
D, A, and B become the
sets A, B, C, and D respectively. When c≡7(mod 8), the sets
D, C, B, and A become the sets A, B,
C, and D respectively. For example, when c=-1, the
limbs in A end in odd natural numbers that are congruent to 7 modulo 8, the
limbs in B end in odd natural numbers that are congruent to 5 modulo 8, the
limbs in C end in odd natural numbers that are congruent to 3 modulo 8, and the
limbs in D end in odd natural numbers that are congruent to 1 modulo 8.) Let
T denote the set of limbs
ending in an element {2k+1+1, 2k+1+3, 2k+1+5,
..., 3∙2k-1} (these are one-element limbs). Let U denote the
set of limbs ending in an element of {[3(2k+5)+1]/2, [3(2k+13)+1]/2,
[3(2k+21)+1]/2, ..., [3(2k+1-3)+1]/2} (these are
one-element limbs). (When c is congruent to 1 modulo 6, the U
set is the
same. When c is congruent to 5 modulo 6, U is the set of limbs ending in
an element of {[3(2k+1)+5]/2, [3(2k+9)+5]/2, [3(2k+17)+5]/2,
..., [3(2k+1-7)+5]/2}.) Also, let S denote the set of limbs ending in an element of {2k+1, 2k+3,
2k+5, ..., 2k+1-1}. The 3n+c
process will be illustrated for k=5, 6, and 7.
The limb comprising E for k=6 and c=-1 is (118, 88) where the
first element in the parentheses denotes the beginning element in the 3n+c
sequence and the second element in the parentheses denotes the ending element. The limbs comprising
F are (96, 4), (144, 28), (120,
16), (108, 40), (156, 64), (102, 76), and (126, 52), the limbs comprising
G are (2, 1) and (20, 7), the limbs comprising T are (129), (131), (133),
..., (191), and the limbs comprising U are (100), (112), (124), (136), (148),
(160), (172), and (184). In the following table, "a 2 (142, 71)→106(A)",
for example, denotes that the limb is not dead (denoted by "a"), has 2 elements,
and attaches to 106 (the first element of a limb in A).
"d " denotes that the limb is dead. The limbs in A,
B, C, and D (in the four columns
respectively) are;
a 2 (142, 71)→106(A)
d 2 (138, 69)→103(A) d 5 (180,
67)→100(U) a 2 (130, 65)→97(D)
a 4 (106, 79)→118(E)
a 2 (154, 77)→115(C) d 2 (150, 75)→112(U)
d 7 (132, 73)→109(B)
d 2 (174, 87)→130(D) d
4 (114, 85)→127(A) a 2 (166, 83)→124(U)
d 2 (162, 81)→121(D)
a 2 (190, 95)→142(A)
d 2 (186, 93)→139(T)
d 25 (168, 91)→136(U)
a 2 (178, 89)→133(T)
a 1 (103)→154(B)
a 1 (101)→151(T)
d 1 (99)→148(U)
a 1 (97)→145(T)
d 1 (111)→166(C)
a 1 (109)→163(T)
a
1 (107)→160(U)
d 1 (105)→157(T)
a 1 (119)→178(D)
d 1 (117)→175(T)
a 1 (115)→172(U)
a 1 (113)→169(T)
a 1 (127)→190(A)
a 1 (125)→187(T)
d 1 (123)→184(U)
a 1 (121)→181(T)
For k=7 and c=1, the limbs comprising E are (194, 188) and (218,164), the limbs
comprising F are (192, 8), (288, 20), (240, 80), (336, 32), (264, 44), (312,
152), (360, 68), (204, 116), (228, 56), (276, 104), (300, 28), (324, 92), (372,
140), and (234, 176), the limbs comprising U are (200), (212), (224), ..., (380),
and the limbs comprising T are (257), (259), (261), ..., (383). The limbs
in A, B, C, and D consisting of more than one element are;
d 2 (258, 129)→194(E)
d 5 (348, 131)→197(C) a 2 (266, 133)→200(U)
d 2 (270,135)→203(B)
a 7 (242, 137)→206(B)
a 2 (278,
139)→209(A) d 2 (282, 141)→212(U)
d 7 (252, 143)→215(D)
a 2 (290, 145)→218(E)
d 2 (294,
147)→221(C) d 4 (198, 149)→224(U)
a 2 (302, 151)→227(B)
d 2 (306, 153)→230(C)
a 4 (206,
155)→233(A) a 2 (314, 157)→236(U)
d 2 (318, 159)→239(D)
d 17 (216, 161)→242(A)
a 2 (326,
163)→245(C) d 2 (330, 165)→248(U)
d 4 (222, 167)→251(B)
a 2 (338, 169)→254(D)
d 2 (342,
171)→257(T) a 4 (230, 173)→260(U)
a 2 (350, 175)→263(T)
d 2 (354, 177)→266(C)
d 9 (210,
179)→269(T) a 2 (362, 181)→272(U)
d 2 (366, 183)→275(T)
d 4 (246, 185)→278(B)
a 2 (374,
187)→281(T) d 2 (378, 189)→284(U)
a 4 (254, 191)→287(T)
When c=5 and k=5, the limbs in A, B, C, and
D consisting of more than one element are;
a 7 (58, 37)→58(A),
d 2 (78, 39)→61(A)
d 2 (66, 33)→52(U)
a 2 (70, 35)→55(D)
d 2 (90, 45)→70(D),
a 2 (94, 47)→73(T)
a 2 (82, 41)→64(U)
d 4 (54, 43)→67(T)
When c=11 and k=5, the limbs in A, B, C, and
D consisting of more than one element are;
a 2 (70, 35)→58(G),
d 2 (66, 33)→55(C)
d 2 (78, 39)→64(U)
d 5 (84, 37)→61(D)
d 14 (48, 43)→70(A),
a 2 (84, 41)→67(T)
a 2 (94, 47)→76(U)
d 2 (90, 45)→73(T)
The tables above show which types of limbs attach to other types of limbs and
that only a limb in A can attach to itself at its beginning (of course,
this hasn't been proven). Suppose i is the last element of a
two-element limb in S. A two element limb in S cannot attach
to itself at its beginning (except possibly for one order per c value)
since (3i+c)/2 equals 2i only if i=c. An
empirical result is;
(59) If a limb in S is not dead and has more than one element, then
the second element is odd.
Suppose i is the last element of a four-element limb in S.
In a four-element limb in S, the first and third elements are even and
the second and fourth elements are odd. A four-element limb in S
cannot attach to itself at its beginning (except possibly for one order when
c=-1) since (3i+c)/2 equals 2(2i-c)/3 only if i=-7c.
Usually, a limb in A cannot attach to itself at its beginning since the
limb is either dead, a one-element limb, a two element limb, or a four-element
limb. Usually, limbs in S do not attach to other limbs of equal
length. When c=1 or -1, two-element, four-element, seven-element,
twelve-element, seventeen-element, twenty-element, twenty-five element, and
other longer length limbs in A sometimes attach to other limbs of equal
length in A, B, C, or D. When c=1 or
-1, a seven-element limb in A that attaches to a limb of equal length in
A, B, C, or D is dead (this is an empirical result).
For c=1 and k=18, the only limb in A that is not dead, does
not consist of two or four elements, and that attaches to another limb in A
with the same length is (484034, 306305). This limb has a length of 12 and
attaches to the limb (459458, 290753). For c=1 and k=20, the
only limb in A that is not dead, does not consist of two or four
elements, and that attaches to another limb in A with the same length is
(2056898, 1301633). This limb also has a length of 12. If c=-1, 11, 13, 25, 29, 31, 41, 43, 47, 59, 61, 73,
77, 79, 89, 91, or 95 (or larger unspecified values), let Ao denote
the limbs in A where the integer portion of the last element of the limb divided by 8 is even (and let
Ae
denote the remaining limbs in A), or if c=1, 5, 7, 17, 19, 23, 25, 35, 37, 49,
53, 55, 65, 67, 71, 83, 85, or 97 (or larger unspecified values), let Ao
denote the limbs in A where the integer portion of the last element of the limb divided by 8 is odd
(and let Ae denote the remaining limbs in A).
Another empirical result is;
(60) A limb in Ao attaches to a two-element or four-element limb
in A, B, C, or D.
This property further reduces the probability of a limb in S attaching to
itself at its beginning.
More Properties of Least-Residue Trees
In this section, c is restricted to being 1 or -1. (This is for
the purpose of comparing 3n+1 and 3n-1 sequences; many of the
properties to be given usually still apply for c>1.) Some
empirical results are;
(61) If c=1, no limb in a least residue tree other than {4, 2, 1} ends in an odd natural number
less than 2k (in the case of {4, 2, 1}, 1 is less than 2k
for the order of 6). If c=-1, no limbs in a least residue tree
other than {2, 1} and {20, 10,
5, 14, 7} end in an odd natural number less than 2k (in the
case of {2, 1}, 1 is less than 2k for the order of 6 and in
the case of {20, 10, 5, 14, 7}, 7 is less than 2k for the
order of 24). (When c=-1 and k=2, the limb (10, 5) [in B]
attaches to the limb (7) [in A], and the limb (7) attaches to the limb
(10, 5). [There are no limbs in C, D, or U in this
case.] When k=3, the limb in F is (12, 4), the limbs in G
are (2, 1) and (20, 7), the limbs in S are (18, 9), (22, 11), (13), and
(15), the limbs in T are (17), (19), (21), and (23), and the limb in U
is (16). In essence, trivial cycles occur before the 3n+c
process is fully in effect. Note that
the dead limb {..., 54, 27, 80, 40} attaches to the limb {20, 10, 5, 14, 7} for k>3,
so that the limbs in G could be viewed as being absorbed by dead limbs.)
(62) If k>2, there are 2k-3 limbs in A,
B, C, or D.
(63) If k>2, there are 2k-3 limbs in E and
F.
(64) If k>4, a fourth of the limbs in A attach to four-element limbs.
(65) If a limb in A ends in the natural number i where (3i+c)/2>2k+1,
then the limb attaches to a two-element limb.
(66) The fourth element of a limb in E is even (there are at least four
elements in a limb in E).
(67) A four-element limb in Ae cannot attach to a four-element
limb in A, B, C, or D.
(68) A two-element limb in Ao cannot attach to a two-element
limb in A or C.
(69) There are no limbs in E with lengths of 2, 3, 5, 6, 8, or 11.
The many common properties of the least-residue trees of the 3n+1 and 3n-1
sequences indicate that it would be more logical to allow negative n
values and consider the two sequences to be the same sequence.
Other Cycles in Least-Residue Trees
Besides trivial cycles and limbs in A attaching to themselves at
their beginning (as for the previously shown limb (58, 37) for c=5 and
k=5), cycles can also be formed from limbs in F.
When c=-1 and k=6, the limb (168, 91) (in C) attaches to 136 (in
U) and when
k=7, the limb {336, 168, ..., 91, 272, 136} contains 68 (136/2) and is in
F.
When c=5, the sequence 187, 566, 283, ..., 187 (consisting of 44 distinct
elements) is not an "odd" path. When c=5 and k=10, the limb (2076, 1327) (in
B) attaches to 1993 (in C) and when k=11, the limb {4152, 2076, ..., 1327, 3986,
1993, 5984, 2992} is in F. When k=11, the limb (3936, 2461) in (A)
attaches to 3694 (in A). When k=12, the two dead limbs {8304, 4152, 2076,
..., 519, 1562, ..., 374} and {7872, 3936, 1968, ..., 123, 374, ..., 1562}
form a cycle (containing all of 187, 566, 283, ..., 187) where the attachment
points are immediately after the odd natural numbers divisible by 3.
When c=5, the sequence
347, 1046, 523, ..., 347 (consisting of 44 distinct elements) is not an "odd path". When
k=12, the two dead
limbs {7632, 3816, 1908, ..., 477, 1436, ..., 1334} and {7088, 3544, 1772, ...,
443, 1334, ..., 1436} form a cycle (containing all of 347, 1046, 523, ..., 347)
where the attachment points are immediately after the odd natural numbers
divisible by 3.
Limit Relationships in Least-Residue Trees and a Diophantine Equation
In this section, c is restricted to being 1 or -1.
Most of the results in this section are empirically derived. Let y denote the first element of a limb in S and let z
denote the first element of the limb that the limb in S
attaches to. Let x denote y-z. x/y is largely fixed for a particular
limb length; these ratios approach limits as k approaches infinity. The
x/y values for limbs that aren't dead approach their limits monotonically, that
is, if c>0, then the
maximum x/y value of live limbs of a given length for a given order is less than
the maximum x/y value of live limbs of the given length for a larger order, and
the minimum x/y value of live limbs of a given length for a given order is less
than the minimum x/y value of live limbs of the given length for a larger order.
Similarly, if c<0,
then the maximum x/y value of live limbs of a given length for a given order is
greater than the maximum x/y value of live limbs of the given length for a
larger order, and the minimum x/y value of live limbs of a given length for a
given order is greater than the minimum x/y value of live limbs of the given
length for a larger order. The
limits for limb lengths of 1, 2, 4, 5, 7, 9, 10, 12, 14, 15, 17, 18, 20, 22, 23,
and 25 are -1/2, 1/4, -1/8, 7/16, 5/32, -17/64, 47/128, 13/256, -217/512, 295/1024,
-139/2048, 1909/4096, 1631/8192, -3299/16384, 13085/32768, and 6487/65536
respectively. When c=1, the x/y values approach their
limits from below, so x values for limb lengths where the limits are
negative (1, 4, 9, 14, 17, 22, ...) can never reach 0. Similarly, when
c=-1, the x/y values approach their limits from above, so x
values for limb lengths where the limits are positive (2, 5, 7, 10, 12, 15, 18,
20, 23, 25, ...) can never reach 0. (Note that not all limb lengths are permissible.
Lengths less than or equal to 101 that aren't permissible are 3, 6, 8, 11, 13,
16, 19, 21, 24, 26, 29, 32, 34, 37, 39, 42, 44, 47, 50, 52, 55, 57, 60, 63, 65,
68, 70, 73, 75, 78, 81, 83, 86, 88, 91, 94, 96, 99, and 101.)
Additionally, x and y have to be solutions of the Diophantine equation
ny-dx=ce
for some n, d, and e values that are fixed for a particular limb length.
The
e
values for limb lengths up to 18 are;
length=1, e=1
length=2, e=2
length=4, e=10
length=5, e=20
length=7, e=76, 58
length=9, e=260, 206
length=10, e=520, 412, 340
length=12, e=1688, 1364, 1148, 1004, 986, 842
length=14, e=5320, 4348, 3700, 3268, 3214, 2782
length=15, e=10640, 8696, 7400, 6536, 6428, 5960, 5564, 4988, 4916, 4340
length=17, e=32944, 27112, 23224, 20632, 20308, 18904, 17752, 17716, 15988,
15772, 14836, 14314, 14044, 12892, 12748, 12586, 11596, 11434, 11290, 10138
length=18, e=65888, 54224, 46448, 41264, 40616, 37808, 35504, 35432, 31976,
31544, 29672, 28628, 28088, 25784, 25496, 25172, 23192, 22868, 22580, 20276
Note that there are "consecutive length" pairs (1 and 2, 4 and 5, 9 and 10, 14
and 15, 17 and 18, ...) and that two times an e value for the smaller length of
the pair is an e value for the larger length of the pair. Other than a
length of 2, an e value for the larger length of the pair is divisible by 4.
(Generalized dead limbs were previously discussed in connection with the
properties of 3n+c cycles. When the element after an odd
element i in a generalized dead limb is defined to be 3i+1, the
lengths of generalized dead limbs that aren't permissible are 3, 6, 11, 16, 19,
24, 29, 32, 37, 42, 47, 50, 55, 60, 63, 68, 73, 78, 81, 86, 91, 94, 99, 104,
.... The permissible lengths of generalized dead limbs include the
permissible lengths of the limbs in S. New permissible lengths [in
the generalized dead limbs] are three larger than the second element of a
consecutive-length pair in S.)
The origin of the Diophantine equation ny-dx=ce can be understood by using the
previously mentioned formula s=(Xa-cZ)/Y.
Let i denote the last element of a limb in S and let
a=(3i+c)/2. Then x=(Xa-cZ)/Y-a,
y=(Xa-cZ)/Y, n=X-Y, and d=X.
Substituting into the equation ny-dx=ce and simplifying gives
e=Z. Limbs in S having more than one element satisfy
the Diophantine equation n(y/2)-(d/2)x=c(e/2)
where d/2 is even. By Proposition (59), y/2 is odd when the
limb is not dead, so e/2 must be odd. Limbs with lengths of 5, 10,
15, 18, 23, ... (where the e values are divisible by 4) must then be
dead.
x>0 for limbs with positive x/y limits and x<0 for limbs with negative
x/y limits (an empirical result), so a limb in S cannot attach to itself at its beginning.
Also, y>order/2, therefore x=0 implies n(order/2)<ce,
c>0, n>0, or
(-n)(order/2)<(-c)e, c<0, n<0, a contradiction (based on empirical
evidence).
(Apparently, it is not necessary to solve the Diophantine equation ny=ce to
arrive at a contradiction.) Proving that n(order/2)>ce,
c>0, n>0, or
(-n)(order/2)>(-c)e, c<0, n<0, would require finding the smallest order for
which a given e value of a given limb length occurs. Let order1
denote the smallest order for which a given limb length occurs and let e11,
e21, e31, ..., ei1 denote the
e values that
occur for this order. Let e12, e22,
e32,
..., ej2 denote the remaining e values that occur for the given limb
length and 2∙order1, let e13,
e23,
e33, ..., ek3 denote the remaining e values that occur for
the given limb length and 4∙order1, etc. If c>0 and
n>0,
n(order1/2) is so much greater than ce11 for example, that
n(order1/2)-ce11, n(order1/2)-ce21,
n(order1/2)-ce31, ..., n(order1/2)-cei1
are all approximately equal. Similarly, n(2∙order1/2)-ce12,
n(2∙order1/2)-ce22, n(2∙order1/2)-ce32,
..., n(2∙order1/2)-cej2 are all approximately equal and
approximately twice as large as the differences for order1.
Similar empirical results apply for c<0 and n<0.
The first step in proving that x cannot equal 0 is to find a formula for n.
This paragraph applies for limbs in S. For a limb length of 12,
X=28 and Y=35, for a limb length
of 25, X=216 and Y=310, for a limb length of 38,
X=224
and Y=315, ..., and for a limb length of 181, X=2112 and
Y=370. (Note that 28-35>1, so
that 28i-35i>1
where i is a natural number and hence the limits for limb lengths of the form 13m-1
where m is a natural number less than or equal to 14 are positive.) Blocks of eight
adjacent limb lengths starting with a length of 1 and ending with a length of
181 consist of five types; an
example of the first type is {1, 2, 4, 5, 7, 9, 10, 12}, an example of the
second
type is {40, 41, 43, 45, 46, 48, 49, 51}, an example of the third type is
{66, 67, 69, 71, 72, 74, 76, 77}, an example of the fourth type is {105, 107,
108, 110, 111, 113, 115, 116}, and an example of the fifth type is {144, 146,
147, 149, 151, 152, 154, 155}. There are exactly three pairs of
numerically consecutive limb lengths in each type. Denote the types by
I, J, K,
L, and M. The types of blocks of eight adjacent limb lengths starting with
a length of 1 and ending with a length of 181 are I, I, I,
J, J, K, K, K, L, L,
L, M, M, and M. (In these blocks of eight adjacent limb lengths, the first
limb length of a block is of the form 13m+1 where
m is a
non-negative integer.) The n values for the
first type are 28i-7-35i-4, 28i-6-35i-4,
28i-5-35i-3, 28i-4-35i-3, 28i-3-35i-2,
28i-2-35i-1, 28i-1-35i-1, and 28i-35i
respectively, i=1, 2, and 3. The n values for the second type are 28i-7-35i-4,
28i-6-35i-4, 28i-5-35i-3, 28i-4-35i-2,
28i-3-35i-2, 28i-2-35i-1, 28i-1-35i-1,
and 28i-35i respectively, i=4 and 5. The n values for the third
type are 28i-7-35i-4, 28i-6-35i-4, 28i-5-35i-3,
28i-4-35i-2, 28i-3-35i-2, 28i-2-35i-1,
28i-1-35i, and 28i-35i respectively,
i=6, 7, and 8.
The n values for the fourth type are 28i-7-35i-4, 28i-6-35i-3,
28i-5-35i-3, 28i-4-35i-2, 28i-3-35i-2,
28i-2-35i-1, 28i-1-35i, and 28i-35i
respectively, i=9, 10, and 11. The n values for the fifth type are 28i-7-35i-4,
28i-6-35i-3, 28i-5-35i-3, 28i-4-35i-2,
28i-3-35i-1, 28i-2-35i-1, 28i-1-35i,
and 28i-35i respectively, i=12, 13, and 14. Blocks
of eight adjacent limb lengths starting with a length of 182 and ending with a
length of 336 consist of five types. An example of the first type is {182,
183, 185, 186, 188, 190, 191, 193}, an example of the second type is {208, 209,
211, 213, 214, 216, 217, 219}, an example of the third type is {234, 235, 237,
239, 240, 242, 244, 245}, an example of the fourth type is {286, 288, 289, 291,
292, 294, 296, 297}, and an example of the fifth type is {312, 314, 315, 317,
319, 320, 322, 323}. Denote these types by I', J', K',
L', and M'.
The types of blocks of eight adjacent limb lengths starting with a length of 182
and ending with a length of 336 are I', I', J', J',
K', K', K', K', L', L', M',
and M'. There are exactly three pairs of numerically consecutive limb
lengths in each type. In these blocks of eight adjacent limb lengths, the
first limb length of a block is of the form 13m where
m is
a natural number. The n values for the first type are 28i-8-35i-4,
28i-7-35i-4, 28i-6-35i-3, 28i-5-35i-3,
28i-4-35i-2, 28i-3-35i-1, 28i-2-35i-1,
and 28i-1-35i respectively, i=15 and 16. The
n
values for the second type are 28i-8-35i-4, 28i-7-35i-4,
28i-6-35i-3, 28i-5-35i-2, 28i-4-35i-2,
28i-3-35i-1, 28i-2-35i-1, and 28i-1-35i
respectively, i=17 and 18. The n values for the third type are 28i-8-35i-4,
28i-7-35i-4, 28i-6-35i-3, 28i-5-35i-2,
28i-4-35i-2, 28i-3-35i-1, 28i-2-35i,
and 28i-1-35i respectively, i=19, 20, 21, and 22.
The n values for the fourth type are 28i-8-35i-4, 28i-7-35i-3,
28i-6-35i-3, 28i-5-35i-2, 28i-4-35i-2,
28i-3-35i-1, 28i-2-35i, and 28i-1-35i
respectively, i=23 and 24. The n values for the fifth type are 28i-8-35i-4,
28i-7-35i-3, 28i-6-35i-3, 28i-5-35i-2,
28i-4-35i-1, 28i-3-35i-1, 28i-2-35i,
and 28i-1-35i respectively, i=25 and 26. Blocks of eight adjacent limb lengths
starting with a length of 338 and ending with a length of 454 consist of three
types; an example of the first type is {338, 340, 341, 343, 345, 346, 348, 350},
an example of the second type is {377, 379, 381, 382, 384, 385, 387, 389}, and
an example of the third type is {416, 418, 420, 421, 423, 425, 426, 428}.
There are exactly two pairs of numerically consecutive limb lengths
in each type (the last limb length in a block and the first limb length in the
next block are numerically consecutive) and the first limb length of a block is of the form 13m where
m is
a natural number. Denote these types by N, O, and P. The types of
blocks of eight adjacent limb lengths starting with a length of 338 and ending
with a length of 454 are N, N, N, O, O, O,
P, P, and P. The n values
for the first type are 28i-8-35i-4, 28i-7-35i-3,
28i-6-35i-3, 28i-5-35i-2, 28i-4-35i-1,
28i-3-35i-1, 28i-2-35i, and 28i-1-35i+1
respectively, i=27, 28, and 29. The n values for the second type are 28i-8-35i-4,
28i-7-35i-3, 28i-6-35i-2, 28i-5-35i-2,
28i-4-35i-1, 28i-3-35i-1, 28i-2-35i,
and 28i-1-35i+1 respectively, i=30, 31, and 32. The
n
values for the third type are 28i-8-35i-4, 28i-7-35i-3,
28i-6-35i-2, 28i-5-35i-2, 28i-4-35i-1,
28i-3-35i, 28i-2-35i, and 28i-1-35i+1
respectively, i=33, 34, and 35. An example of the type of blocks starting
with a limb length of 456 is (456, 457, 459, 460, 462, 464, 465, 467).
(There is a limb length of 455, but this limb length is considered to be
associated with the previous block.) There are exactly three pairs of
numerically consecutive limb lengths in each type and the first limb length of a
block is of the form 13m+1 where m is a natural number.
The formula for the n values is valid for small limb lengths but gradually
requires adjustments. Let a denote the number of 2's in a sequence
vector of a live limb in S and b the number of 1's in the sequence vector
(a and b are fixed for a particular limb length). The formula comes from the recursive algorithm for
generating the a and b values corresponding to limb lengths of 2, 4, 7, 9,
12, 14, 17, 20, 22, 25, 27, 30, 33, 35, 38, 40, ..., (that is, limb lengths where not all of the limbs are dead).
This algorithm is as follows. Set x to 1/2 and a and b to 0. If
x is less than
1, set x to 3/2 times x and increment b, otherwise set x to 3/4 times
x and
increment a. (See "Power Fractional Parts" at Wolfram Mathworld [http://www.mathworld.wolfram.com/PowerFractionalParts.html]
for a discussion of the inequality frac[(3/2)N]≤1-(3/4)N
and its relationship to Waring's problem and Collatz 1-cycles.) The a
values for limb lengths of 2, 4, 7, 9, 12, 14, 17, 20, 22, 25, 27, 30, 33, 35,
38, and 40 are 0, 0, 1, 1, 2, 2, 3, 4, 4, 5, 5, 6, 7, 7, 8, and 8 respectively
and the b values are 1, 2, 2, 3, 3, 4, 4, 4, 5, 5, 6, 6, 6, 7, 7, and 8
respectively. A steady-state where 5a is approximately equal to 7b is attained
since 35
is approximately equal to 28. Note that the recursive algorithm
has been defined for 1-2 sequence vectors; the 3/2 factor corresponds to the
"gain" due to a 1 in the sequence vector and the 3/4 factor corresponds to the
"loss" due to a 2 in the sequence vector. When the element after an odd
element i is defined to be (3i+1)/2, the number of even elements
in a live limb is a and the number of odd elements is a+b.
If a limb attached to itself at its beginning, the length of the cycle would be
2a+b+1. Empirical evidence indicates that (2a+b)/(a+b)
is approximately equal to log(3)/log(2). As previously seen, this
irrational number (equal to log2(3)) frequently arises in 3n+1
cycle theory. Crandall showed (in his 1978 article) that if the main
conjecture is true (that the cardinality of the "trajectory" of an odd natural
number is finite), then powers of two and three tend to be poor approximations
of each other. In imprecise terms, log2(3) must then be
difficult to approximate with rational numbers. A parity vector is defined
to be "admissible" when the sum of the elements in the vector equals the
greatest integer in the length times θ where θ equals log(2)/log(3). For
limbs having a length of 2a+b and containing a+b odd
elements, the parity vectors are almost admissible. If another 0 is
included in the parity vector (corresponding to a cycle), limbs with lengths of
2, 7, 12, 20, 25, 33, 38, ... (in the old way of defining the length and before
the length is incremented by 1) are admissible. Quoting from Lagarias'
1985 article, Terras' "Theorem C" is;
(a) The set of integers with coefficient stopping time k are
exactly the set of integers in those congruence classes n (mod 2k)
for which there is an admissible vector v of length k with n=n0(v).
(b) Let n=n0(v) for some vector v
of length k. If v is admissible, then all sufficiently large
integers congruent to n (mod 2k) have stopping time
k. If v is not admissible, then only finitely many integers
congruent to n (mod 2k) have stopping time k.
By part (b) of Terras' theorem, if y were congruent to n=n0(v)
modulo 2k (for an admissible parity vector v having a
length of k=2a+b+1) for a large order
of least-residue tree, then the stopping time would be k, a contradiction (since
y/2 is less than y). As will be shown, there is a simpler way to arrive
at the conclusion that a live limb in S of a given length (and with an
arbitrary starting value y) cannot attach to itself at its beginning for
a sufficiently large order of least-residue tree. Limbs with lengths of 4, 9, 14, 17, 22, 27, 30, 35,
... (in the old way of defining the length and before the length is incremented
by 1) are still not admissible, but n (defined to equal X-Y)
is negative for these lengths.
For limb lengths of 2, 4, 9, 14, 22, 27, 35, 40, ..., the maximum z
value divided by the minimum y value for live limbs associated with a
given sequence vector is less than 3/2 and for limb lengths of 7, 12, 17, 20,
25, 30, 33, 38, ...., the minimum z value divided by the maximum y
value for live limbs associated with a given sequence vector is greater than
3/4. For live limbs with lengths of 4, 9, 14, 22, 27, ... (where the b
values are 2, 3, 4, 5, 6, ... respectively and the b values for the next
smaller limb lengths are 1, 2, 3, 4, 5, ..., respectively), the upper bound of
the maximum y value to order ratio associated with the sequence vector
giving the largest e value is (3/4)X/Y. (For large
orders, the maximum y value to order ratio is approximately equal to the
upper bound, and as the order decreases, the maximum y value to order
ratio gradually decreases [but not monotonically].) For some limb lengths,
the upper bound of the maximum y value to order ratio associated with a
group of sequence vectors is different from the upper bounds associated with
other groups of sequence vectors. (As will be shown, these groups of
sequence vectors are the same as those giving different frequencies of
occurrence of live limbs.) For example, for a live limb with a length of
12, the upper bound of the maximum y value to order ratio associated with
the sequence vector giving the largest e value is 2/3((3/4)X/Y
for a live with a length of 4) and the upper bound of the maximum y value
to order ratio associated with the sequence vector giving the smallest e
value is 16/27 ((3/4)X/Y for a live limb with a length of 9).
For a live limb with a length of 17, the upper bound of the maximum y
value to order ratio associated with two sequence vectors (one of which is the
sequence vector giving the largest e value) is 2/3 ((3/4)X/Y
for a live limb with a length of 4), the upper bound of the maximum y
value to order ratio associated with two other sequence vectors (one of which is
the sequence vector giving the smallest e value) is 128/243 ((3/4)X/Y
for a live limb with a length of 14), and the upper bound of the maximum y
value to order ratio associated with the remaining sequence vector is 16/27
((3/4)X/Y for a live limb with a length of 9). The upper
bound of the maximum y value to order ratio associated with any sequence
vector of a live limb of a given length is one of 2/3, 16/27, 128/243,
4096/6561, 32768/50949, ....
These n values can then be substituted into the inequality n(order/2)>ce,
c>0,
n>0, or (-n)(order/2)>(-c)e, c<0,
n<0. The next step is to
find the maximum e value for a given limb length. Each sequence vector corresponds to
exactly one e value (unproven as yet). Denote the sequence vector array by v (where the array is indexed starting
with 0). Denote the number of elements in a sequence vector by l
and the sum of the elements in the sequence vector by s. The length of
the limb is then l+s, the Y value of the limb is 3l,
and the X value of the limb is 2s+1. The
e
value of the limb is ∑3i∙2m
where the summation is from i=0 to l-1 and where m=∑vj and the summation
is from j=0 to l-1-i. The maximum e value for a given limb length
then occurs when the 2's are at the beginning of the sequence vector
(for a limb that is not dead, there is a single 1 at the beginning of the
sequence vector and the 2's must follow this 1). The first odd element
o in the limb
after the 2's in the sequence vector is [(y/2)(3/4)a]+1 if
c=1 or [(y/2)(3/4)a] if c=-1 where the brackets denote the greatest integer
function. The 1's in the sequence vector (not counting the
initial 1) correspond to a jump (which goes beyond the end of the limb).
The first element of the limb that the limb attaches to is then z=(3/2)b(o+c)-c.
The e value is then (zX-yY)/c. (The 2's in the sequence vector
decrease the limb elements and the 1's in the sequence vector compensate for
this by increasing the limb elements until the last element of the limb is
greater than order/3.)
For a live limb in S, (y/2)(3/4)a(3/2)b+δ=z
where δ is relatively small and positive if c≥1 or negative if
c=-1. x=0 then implies 1=(1/2)(3/4)a(3/2)b+δ/y.
3a+b/22a+b+1=Y/X, so whether
x can equal 0 depends on how
close n gets to 0 (x=0 implies n=X(δ/y)).
(Approximating powers of 2 with powers of 3 becomes relevant at this point.) For a given order, the largest |X(δ/y)| values
correspond to the sequence vector giving the largest e value,
so the largest |X(δ/y)| values are easily quantifiable (the
X(δ/y) values only depend
on the y values due to the greatest integer function). As the order
increases, the |X(δ/y)| values decrease. For example, for
c=1 and a limb
length of 25, the first live limbs occur when the order equals 393216.
Live limbs occur that correspond to the ninth largest e value (for live limbs)
and the fourteenth largest e value (for live limbs) and the respective
X(δ/y)
values are 2.624163 and 2.292368. For an order of 786432, live limbs occur
that correspond to the largest e value, the fourth largest e value, the sixth
largest e value, the seventh largest e value, the eleventh largest
e value, the twelveth largest e value, the seventeenth largest
e value, and the eighteenth
largest e value and the respective X(δ/y) values are 1.693732, 1.415807,
1.285766, 1.281626, 1.156335, 1.135663, 1.079423, and 1.011811. The n
value for this limb length is 6487. Since y>order/2, an upper bound for
|X(δ/y)| (valid for both c=1 and c=-1) is 22a+b+2-k((2(3/2)b-1)/3)
(when a>0). This can be used to
find small orders for which n>X(δ/y) if c=1
or -n>X(-δ/y) if c=-1. For live limbs with a length of 25,
a=5, b=5, and
6487 is greater than the upper bound until k=6. The smallest k values such
that n is greater than the upper bound of X(δ/y),
c>0, n>0, for live limbs with
lengths of 7, 12, and 20 are 4, 7, and 5 respectively.
In his 1978 article, Crandall used continued fractions to show that if
m>1 and Ck(m)=m,
then k>17985 (C(x) is defined to be (3x+1)/2e(x) where 2e(x) is the highest
power of two dividing 3x+1). The following lemma is used. Let 1<m=inf
Tm
and let k be the period of the trajectory Tm. Then
m<k(3+1/m)k-1/(2A(k)-3k)
(where A(k) [due to typographical difficulties, A(k) is
used to denote Ak] is a sum of positive integer sequence values).
For a live limb in S, this gives m<(a+b)(3+1/m)a+b-1/(22a+b+1-3a+b)
where a and b are generated from the recursive algorithm above.
The elements of a live limb in S with a length less than or equal to 20 are
greater than order/12. (In general, the lower bound of the elements of the
limb depends on the sequence vector giving the maximum e value. For
example, for a limb length of 22, (1/4)(3/4)4<1/2.) The largest k values for
which 2k-2<(a+b)(3+1/2k-2)a+b-1/(22a+b+1-3a+b)
for live limbs with lengths of 7, 12, and 20 are 4, 7, and 5 respectively. (a+b)3a+b-1/(22a+b+1-3a+b)
does not grow very fast as a and b increase, so the
maximum order for which a
cycle might occur can be approximated fairly accurately. The difficulty
with this approach (and the above approach) is that small orders have to be checked for
cycles for every
limb length.
More miscellaneous results pertaining to allowable (not necessarily admissible) sequence vectors and the maximum
e values are discussed in this section. The sequence vectors of
limbs in S that aren't dead for lengths of two, four, seven, and nine are (1),
(1, 1), (1, 2, 1), and (1, 2, 1, 1) respectively. The only possible sequence vectors for a live
limb in S with a length of twelve are (1, 2, 2, 1, 1) and (1, 2, 1, 2, 1). The only possible sequence vectors for a live
limb in S with a length of fourteen are (1, 2, 2, 1, 1, 1) and (1, 2, 1, 2, 1,
1). For a live limb in S with a length of 17 or 20, there are
five different sequence vectors. For a live limb in S
with a length of 22, there are nine different sequence
vectors and for a live limb in S with a length of 25, there are nineteen
different sequence vectors. A subset of the sequence vectors for a limb length of 22 is;
(1, 2, 1, 2, 1, 2, 2, 1, 1)
(1, 2, 2, 1, 1, 2, 2, 1, 1)
(1, 2, 2, 1, 2, 1, 2, 1, 1)
(1, 2, 2, 1, 2, 2, 1, 1, 1)
(1, 2, 2, 2, 1, 2, 1, 1, 1)
(1, 2, 2, 2, 2, 1, 1, 1, 1)
The first sequence vector corresponds to the smallest e value for a live limb
and the last sequence vector corresponds to the largest e value for a live limb.
The second sequence vector is obtained from the first sequence vector by
transposing an adjacent 1 and 2, the third sequence vector is obtained from the
second sequence vector by transposing an adjacent 1 and 2, the fourth sequence
vector is obtained from the third sequence vector by transposing an adjacent 1
and 2, etc. until the last
sequence vector is obtained. The number of elements in a sequence vector
is l (9 in this case) and the number of sequence vectors (6) is approximately
equal to l. The 1's and 2's that are transposed gradually move from left
to right in a somewhat regular fashion, wrap around at the third-to-last
sequence vector, and then resume moving from left to right. The minimum
e
value divided by the maximum e value is 0.62636. The
corresponding subset of sequence vectors for a limb length of 25 is;
(1, 2, 1, 2, 2, 1, 2, 1, 2, 1)
(1, 2, 1, 2, 2, 2, 1, 1, 2, 1)
(1, 2, 1, 2, 2, 2, 1, 2, 1, 1)
(1, 2, 2, 1, 2, 2, 1, 2, 1, 1)
(1, 2, 2, 2, 1, 2, 1, 2, 1, 1)
(1, 2, 2, 2, 1, 2, 2, 1, 1, 1)
(1, 2, 2, 2, 2, 1, 2, 1, 1, 1)
(1, 2, 2, 2, 2, 2, 1, 1, 1, 1)
In this case, l=10 and the number of sequence vectors is 8. The minimum
e
value divided by the maximum e value is 0.55595. The
corresponding subset of sequence vectors for a limb length of 27 is;
(1, 2, 1, 2, 1, 2, 2, 1, 2, 1, 1)
(1, 2, 1, 2, 1, 2, 2, 2, 1, 1, 1)
(1, 2, 2, 1, 1, 2, 2, 2, 1, 1, 1)
(1, 2, 2, 1, 2, 1, 2, 2, 1, 1, 1)
(1, 2, 2, 1, 2, 2, 1, 2, 1, 1, 1)
(1, 2, 2, 2, 1, 2, 1, 2, 1, 1, 1)
(1, 2, 2, 2, 1, 2, 2, 1, 1, 1, 1)
(1, 2, 2, 2, 2, 1, 2, 1, 1, 1, 1)
(1, 2, 2, 2, 2, 2, 1, 1, 1, 1, 1)
In this case, l=11 and the number of sequence vectors is 9. The minimum
e
value divided by the maximum e value is 0.53027. The
corresponding subset of sequence vectors for a limb length of 30 is;
(1, 2, 1, 2, 1, 2, 2, 1, 2, 1, 2, 1)
(1, 2, 1, 2, 1, 2, 2, 2, 1, 1, 2, 1)
(1, 2, 1, 2, 1, 2, 2, 2, 1, 2, 1, 1)
(1, 2, 1, 2, 2, 1, 2, 2, 1, 2, 1, 1)
(1, 2, 1, 2, 2, 2, 1, 2, 1, 2, 1, 1)
(1, 2, 1, 2, 2, 2, 2, 1, 1, 2, 1, 1)
(1, 2, 1, 2, 2, 2, 2, 1, 2, 1, 1, 1)
(1, 2, 1, 2, 2, 2, 2, 2, 1, 1, 1, 1)
(1, 2, 2, 1, 2, 2, 2, 2, 1, 1, 1, 1)
(1, 2, 2, 2, 1, 2, 2, 2, 1, 1, 1, 1)
(1, 2, 2, 2, 2, 1, 2, 2, 1, 1, 1, 1)
(1, 2, 2, 2, 2, 2, 1, 2, 1, 1, 1, 1)
(1, 2, 2, 2, 2, 2, 2, 1, 1, 1, 1, 1)
In this case, l=12 and the number of sequence vectors is 13. The 1's and
2's to be transposed move from left to right in a more regular fashion and wrap
around twice. The minimum e value divided by the maximum e value is
0.42839. The corresponding subset of sequence vectors for a limb length
of 33 is;
(1, 2, 2, 1, 2, 1, 2, 2, 1, 2, 1, 2, 1)
(1, 2, 2, 2, 1, 1, 2, 2, 1, 2, 1, 2, 1)
(1, 2, 2, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1)
(1, 2, 2, 2, 2, 1, 1, 2, 1, 2, 1, 2, 1)
(1, 2, 2, 2, 2, 1, 2, 1, 1, 2, 1, 2, 1)
(1, 2, 2, 2, 2, 2, 1, 1, 1, 2, 1, 2, 1)
(1, 2, 2, 2, 2, 2, 1, 1, 2, 1, 1, 2, 1)
(1, 2, 2, 2, 2, 2, 1, 2, 1, 1, 1, 2, 1)
(1, 2, 2, 2, 2, 2, 1, 2, 1, 1, 2, 1, 1)
(1, 2, 2, 2, 2, 2, 2, 1, 1, 1, 2, 1, 1)
(1, 2, 2, 2, 2, 2, 2, 1, 1, 2, 1, 1, 1)
(1, 2, 2, 2, 2, 2, 2, 1, 2, 1, 1, 1, 1)
(1, 2, 2, 2, 2, 2, 2, 2, 1, 1, 1, 1, 1)
In this case, l=13 and the number of sequence vectors is 13. The 1's and 2's to
be transposed wrap around once. Since the length of a sequence vector
approximately equals the number of sequence vectors, the 1's and 2's to be
transposed move on average one position to the right from one sequence vector to
the next (disregarding wrap-around). The minimum e value divided by the maximum
e value is 0.44269 (the minimum e value divided by the maximum
e value
approaches 1/2).
The remaining step is to find the smallest order for which a given e value
occurs. One-half of the limbs in S consist of 1 element, about 1/3 of the limbs in
S consist of two elements, about
1/12 of the limbs in S consist of four elements, about 1/72 of the
limbs in S consist of five elements, about 1/36 of the limbs in
S consist of seven elements, about 5/576 of the limbs in S consist of nine
elements, about 7/864 of the limbs in S consist of ten elements, about 77/7776
of the limbs in S consist of twelve elements, about 13/15552 of the limbs in
S
consist of fourteen elements, and about 815/186624 of the limbs in S consist of
fifteen elements. The denominators of these fractions are a power of two
times a power of three. Denote a fraction by f. The number of limbs in
S
(for an order of 3∙2k, k>2) is 2k-1.
Denote the number of limbs in S of a given length by m. For limb lengths of 2, 4, or 5, 0≤[2k-1f]+1-m≤1,
for limb lengths of 7, 9, or 10, -1≤[2k-1f]+1-m≤2, and for limb
lengths of 12, 14, or 15, -2≤[2k-1f]+1-m≤3, where the brackets denote
the greatest integer function. About 2/3 of the limbs in S with a
length of 1 are alive, about 1/2 of the limbs in S with a length of 2 are alive,
about 1/2 of the limbs in S with a length of 4 are alive, about 1/6 of the limbs
in S with a length of 7 are alive, about 1/3 of the limbs in S with a length of
9 are alive, about 25/154 of the limbs in S with a length of 12 are alive, and
about 1/4 of the limbs in S with a length of 14 are alive. Denote one of
these fractions by f' and denote the number of live limbs in S of a given length
by m'. For limb lengths of 1, 0=[2k-1ff']-m', for limb lengths
of 2, 4, 7, or 9, 0≤[2k-1ff']-m'≤1, and for limb lengths of 12 or 14,
-1≤[2k-1ff']-m'≤2. For longer limb lengths, the
portion of the limbs in S is similarly fixed. The a+b values of the
live limbs
in S with lengths of 2, 4, 7, 9, 12, 14, ..., are 1, 2, 3, 4, 5, 6, ....,
respectively. For
every value of j, j=1, 2, 3, ..., there is a relatively small odd
natural number g, a relatively small natural number h, and a natural number
i
approximately equal to j such that 2k-1(g/(2h
3i)) closely approximates the number of live limbs in
S with
the corresponding length. For live limbs in S with lengths of 17, 20, 22, 25,
27, 30, and 33, the g values are 233, 695, 6349, 3791, 2831, 3425, and 7359 respectively,
the h values are 11, 11, 10, 12, 13, 8, and 13 respectively, and the i values are 5,
8, 10, 9, 9, 12, and 13 respectively. (These values aren't unique; similar
g
and h values can be found when i is set to j.) For some limb lengths, live
limbs associated with certain sequence vectors occur more frequently than live
limbs associated with other sequence vectors. For example, for a limb
length of 12, there is a group of live limbs in S associated with the sequence
vector giving the largest e value where the probability of occurrence is 17/(26∙35)
and there is a group of live limbs in S associated with the sequence vector
giving the smallest e value where the probability of occurrence is 1/(23∙35)
(the sum of these probabilities is 25/(26∙35)). For a limb
length of 17, there is one group of live limbs in S associated with two sequence
vectors (one of which is the sequence vector giving the largest e value) where
the probability of occurrence is 1/(210∙31), another group
of live limbs in S associated with two other sequence vectors (one of which is
the sequence vector giving the smallest e value) where the probability of
occurrence is 13/(210∙35), and another group of live limbs
in S associated with the remaining sequence vector where the probability of
occurrence is 5/(211∙33) (the sum of these probabilities
is 233/(211∙35)). For a limb length of 22, the
probabilities of occurrence for live limbs in S in the different groups are
1147/(28∙310), 5/(213∙33), and 13/(213∙35).
For a limb length of 25, the probabilities of occurrence for live limbs in S in
the different groups are 1237/(211∙39), 853/(212∙39),
and 29/(28∙39). For a limb length of 27, the
probabilities of occurrence for live limbs in S in the different groups are
2567/(213∙39) and 11/(210∙38).
For a limb length of 30, the probabilities of occurrence for live limbs in S in
the different groups are 131/(212∙37), 107/(212∙38),
865/(29∙312), 215/(29∙311), and
185/(210∙311). For limb lengths of 14, 20, or 33,
there is only one group of live limbs in S associated with the different sequence vectors.
The differences between the estimated number of live limbs in S using these
probabilities (where rounding is done) and the actual number of live limbs in
S
for different orders and limb lengths (denoted by L) when
c=1 are;
k=12 13 14
15 16 17 18 19 20
21 22 23 24 25 26
27 28 29 30 31 32
33
L=2 0 1
0 1 0 1
0 1 0 1
0 1 0 1
0 1 0 1
0 1 0 1
4 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0
7 0
0 0 0 1 -1 0 0 0
0 0 0 0
-1 1 -1 0
0 0 0 0
0
9 0
0 1 0 0
1 0 1 0
0 0 0 1
0 0 1 0
0 0 0 1
0
12 0 0
0 0 0 -1
1 -1 1 -1 -1
0 0 0 -1
-1 0 0 0
0 0 0
14 -1 0
0 -1 0 0
-1 0 0 0
0 0 0 0 0 0 -1 0
-1 0 -1 0
17 0 1
1 1 0 1
0 1 -1 1
0 1 0 2
1 1 0 1
0 0 1 0
20 0 -1
0 -1 1 -1
1 0 1 -1
1 -1 1 0
1 -1 0 -1 1 -1 1 -1
22 0 -1
1 0 -3 -1
-2 0 -1 -1
-1 -2 -3 -2 -1
-3 -2 0 1
1 1 2
25 0 0
0 1 2 1 -2 3 0 5
4 4 1 2 0 5 0 -1
-4 1 1 6
27 0 0
0 0 1 -1
1 2 3 -1
0 4 -1 1
2 1 5 2
1 1 0 0
30 0 0
0 0 0 1
3 -3 1 0
-2 -2 -1 1 -2
-2 -2 1 0
1 1 4
33 0 0
0 0 0 0
0 0 -1 1
-1 1 0 -4 1 0 2 -3
2 -5 0 -7
For every order and limb length, the difference between the number of live limbs
in S associated with one sequence vector in a group and the number of live limbs
in S associated with another sequence vector in the group is at most 1. (This
appears to still be true for live limbs in A, B, C, or D or any other similarly constructed subset
of S where the last elements in the limbs are congruent to an odd natural number
j modulo 2i, j<2i , i<k).
The above property can be used to estimate the smallest order for which a live
limb in S with a given length occurs. For example, assuming that the upper
bound of the difference between the estimated and actual number of live limbs
with a length of 25 (where the difference is given by the formula [2k-1(3791/(212∙39))+0.5]-m')
is 6 (a somewhat dubious proposition) gives m'≥1 when k=19 (when
c=1, the
smallest order for which a live limb with a length of 25 occurs is 3∙217).
The n value for a limb length of 25 is 6487 and the largest e value is 811694,
so n(order/2) is much greater than ce, c>0, n>0, when
order=3∙219.
The difficulty with this approach is determining the upper bound of the
difference between the estimated and actual number of live limbs.
When c>1, there are relatively few limbs in S having lengths other than 1, 2, 4,
5, 7, 9, 10, 12, 14, 15, 17, 18, 20, 22, 23, 25, .... When k is
sufficiently large for a given limb length and c value greater than 1, the limbs
in S have many of the above properties.
Another Kind of Least-Residue Tree
In this section, c is restricted to being 1 or -1. Consider a tree
where the order is of the form 3∙2k and no element of a limb is
greater than or equal to the order or divisible by 3. The first element of a limb must be
even and greater than the order divided by 2, the last element of a limb must be
odd and greater than the order divided by 3, and every limb must contain at
least one element that is divisible by 8. (As for a limb in S of a
least-residue tree, a limb cannot attach to its interior or the interior
of another limb.) The possible
lengths of these limbs are 12, 14, 15, 17, 18, 20, 22, 23, .... The
lengths of the limbs are the same as those for a limb in S of a least-residue
tree (except there are no lengths of 1, 2, 4, 5, 7, or 9) and the X and
Y values
are the same. Denote the first element of a limb by y, the last element of
a limb by i, (3i+c)/2 by z, and y-z by
x. As before, x and y satisfy the
Diophantine equation ny-dx=ce where n=X-Y,
d=X, and the e values are fixed for a
given limb length. Some e values are;
length=12, e=1202
length=14, e=3862
length=15, e=7724, 5780
length=17, e=24196, 22738, 18850, 18364, 16906, 16258, 14530, 14476, 13378,
13018
length=18, e=48392, 45476, 37700, 36728, 33812, 32516, 29060, 28952, 26756,
26036
For a given limb length, the largest e value is larger than the largest
e value
for a live limb in S of a least-residue tree (when not all of the limbs are dead
for that length) and the smallest e value (when there is more than one
e value)
is smaller than the largest e value for a live limb in S of a least-residue tree
(when not all the limbs are dead for that length). The lengths of the
sequence vectors for limb lengths of 12, 14, 15, 17, 18, 20, 22, and 23 are 5,
6, 6, 7, 7, 8, 9, and 9 respectively. The largest elements in
the sequence vectors for limb lengths of 12, 14, 15, 17, 18, 20, 22, and 23 are 3, 3,
3, 4, 4, 5, 5, and 5 respectively. For some limb lengths, limbs associated
with certain sequence vectors occur more frequently than limbs associated with
other sequence vectors. For example, for a limb length of 17, the
number of limbs
associated with two sequence vectors is about [2k-1(295/(29∙36))+0.5],
the number of limbs associated with five other sequence
vectors is about [2k-1(5/(210∙31))+0.5], the
number of limbs associated with two other sequence vectors is
about [2k-1(5/(29∙33))+0.5], and the number of limbs associated with the remaining sequence vector is
about [2k-1(13/(210∙35))+0.5]. For every order and limb
length, the difference between the number of limbs associated with one sequence
vector in a group and the number of limbs associated with another sequence
vector in the group is at most 2. For some limb lengths, the upper bound
of the maximum y value to order ratio associated with a group of sequence
vectors is different from the upper bounds associated with other groups of
sequence vectors. (These groups of sequence vectors are the same as those
giving different frequencies of occurrence of limbs.) For example, for a
limb length of 17, the upper bound of the maximum y value to order ratio
associated with two sequence vectors is 512/729, the upper bound of the maximum
y value to order ratio associated with five other sequence vectors is 2/3, the
upper bound of the maximum y value to order ratio associated with two other
sequence vectors is 16/27, and the upper bound of the maximum y value to order
ratio associated with the remaining sequence vector is 128/243. For limb lengths of 12, 14, 15, 17, 18,
20, 22, and 23, the number of limbs can be approximated by [2k-1f+0.5]
where f equals 17/(25∙35), 13/(28∙35),
353/(28∙36), 1057/(29∙36), 695/(29∙37),
6733/(210∙37), 9817/(213∙36), and
56915/(214∙37) respectively. The number of limbs in one of these
trees is approximately equal to the order divided by 144.
m-Cycles
In their 2005 article, Simons and de Weger gave bounds for Λ=(K+L)
log 2 - K log 3 (where K is the total number of odd
elements and L is the total number of even elements in the m-cycle). A corollary
proved is 0<Λ<m/xmin. For a limb in S
of a least-residue tree (with a length of 3a+2b) to attach to
itself at its beginning, this gives xmin<(a+1)/((2a+b+1)
log 2 - (a+b) log 3).
This upper bound for the minimum is about twice as large as the minimum given by
Halbeisen and Hungerbühler's formula. In the next two sections, the upper
bound of the minimum will be computed when it's not computationally feasible to
compute the minimum.
The Minimum in a Collatz Cycle
In this section, c is restricted to being 1 or -1. The results
in this section are mostly empirically derived.
The 1-2 sequence vector (of a limb in S having a length of l and
containing m odd elements) corresponding to a small e value
(possibly the smallest) can be
constructed from ]jm/l[ - ](j-1)m/l[, j=1, 2, 3,
..., l, by
rotating (if necessary) the vector so that a (1, 1) is at the beginning of the
vector and
converting (1, 0)'s to 2's. The last element of the sequence
vector will be a 2 and must be changed to a 1 to match the sequence vector
corresponding to the smallest e value. (Note that this rotation of
the parity vector does not correspond to the parity vector of a limb in S
[since the first element must be even] and that the first element
of a sequence vector just indicates that the first element of the limb is even
[and not that there is an odd natural number in the 3n+c sequence
immediately preceding it]. If a cycle were formed by a limb attaching to itself
at its beginning, the first element of the sequence vector would be changed to a
2 [and the 2 would indicate that there were 2 even elements between odd elements
in the sequence].) For example, for a limb length of 20, the
parity vector must be rotated right by 5 positions for the resulting sequence
vector to
match the sequence vector corresponding to the smallest e value.
(The possible right-rotations for a limb length of 20 are 0, 5, and 10. In
general, the difference between successive right-rotations is 3 or 5.)
The required right-rotations of the parity vector for limb lengths of 2, 4, 7, 9,
12, 14, 17, 20, 22, 25, 27, 30, 33, 38, and 43 are
0, 0, 0, 0, 0, 0, 0, 5, 11, 0, 11, 0, 5, 0, and 0
respectively. If the un-rotated parity vector gives an e
value for a limb in S, then the e value is the smallest for a limb
in S and all the possible right-rotations give e values for limbs in
S. For limb lengths of 20, 22, 27, 33, 35, 40, 45, 48, 51, 53,
and 56, the un-rotated parity vector gives e values too small to be a
limb in S. In these cases, a right-rotation of 5 gives an e
value (usually not the smallest) for a limb in S.
A rotation of the parity vector ]jm/l[ - ](j-1)m/l[,
j=1, 2, 3, ..., l, so that a (1, 0) is at the beginning of the
vector does not correspond to a live limb in S since the second element
of a live limb in S is odd. A rotation of the parity vector so that
a (0, 1) is at the beginning of the vector corresponds to a live limb in S,
but except for limb lengths of 7, 12, 17, 30, 43, ..., the e values given are too
small. For a given limb length, live limbs in S occur for only one
right-rotation of the parity vector ]jm/l[ - ](j-1)m/l[,
j=1, 2, 3, ..., l. (The resulting sequence vectors for limb lengths of 7, 12, 17, 30, and
43
are (1, 2, 1), (1, 2, 1, 2, 1), (1, 2, 1, 2, 1, 2, 1), (1, 2, 1, 2, 1, 2, 2,
1, 2, 1, 2, 1), and (1, 2, 1, 2, 1, 2, 2, 1, 2, 1, 2, 2, 1, 2, 1, 2, 1) respectively.
[For example, for a limb length of 43, the parity vector is 0, 1, 0, 1, 1, 0, 1,
1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, and 1. Changing
the last 1 and the first 0 (a (1, 0)) to a 1 and the other (1, 0)'s to 2's gives the
sequence vector.] These sequence vectors have bilateral
symmetry and are the sequence vectors corresponding to the smallest e
values.)
For limb lengths less than or equal to 51, no limb in S can have the
parity vector ]jm/l[ - ](j-1)m/l[, j=1,
2, 3, ..., l, if l and m are not relatively prime (51 is the largest limb
length where it is computationally feasible to determine this [at least by an
exhaustive search up to relatively large orders of least-residue trees]). For limb lengths of 7,
12, 17, 30, and 43, l and m are relatively prime and there are
limbs in S having the parity vector ]jm/l[ - ](j-1)m/l[,
j=1, 2, 3, ..., l, (the (l, m) values for limb
lengths of 12 and 30 [(8, 5) and (19, 12) respectively] are continued-fraction
convergents of log(3)/log(2)). For limb lengths of 20, 22, 27, 33, 40, and
48, l and m are relatively prime, but there are no limbs in S
having the parity vector ]jm/l[ - ](j-1)m/l[,
j=1, 2, 3, ..., l.
For a live limb in S, the second sequence vector value is a 2 if the
limb length is greater than 4 (so that the parity vector must begin with a (0,
1, 0)). Let v1, v2, v3,
..., vl be a right-rotation of the parity vector ]jm/l[
- ](j-1)m/l[, j=1, 2, 3, ..., l, such that
v1=0, v2=1, and v3=0.
Let s1=1.0 and si+1=(3/2)si
if vi=1 or (1/2)si otherwise, i=1,
2, 3, ..., l-1. Let r denote gcd(l, m).
Requirements for a live limb in S (with a sufficiently large beginning
element y) to have
this right-rotated parity vector are that (1) twice the minimum s value be
greater than the maximum "odd" s value for all possible right-rotations
of the parity vector where v1=0, v2=1, and
v3=0, (2) the difference in successive right-rotations of the
parity vector and the difference in successive indices (modulo l/r)
of the minimum s value must be the same for all possible right-rotations
of the parity vector where v1=0, v2=1, and
v3=0, and (3) the difference in the indices (modulo l/r)
of the minimum and maximum "odd" s values must be the same for all
possible right-rotations of the parity vector where v1=0,
v2=1, and v3=0. Limb lengths satisfying
the first condition for m values less than or equal to 100 are 7, 12,
17, 20, 25, 30, 38, 43, 51, 56, 61, 74, 87, 92, 105, 123, 136, 211, and 242.
Of the first 8192 limb lengths, 20 is the only limb length that satisfies the
first and third conditions, but not the second condition. Of the first
8192 limb lengths, 56 is the only limb length that satisfies the first
condition, but not the second and third conditions. (l, m)
values satisfying the first condition are (5, 3), (8, 5), (11, 7), (13, 8), (16,
10), (19, 12), (24, 15), (27, 17), (32, 20), (35, 22), (38, 24), (46, 29), (54,
34), (57, 36), (65, 41), (76, 48), (84, 53), (130, 82), (149, 94), (168,
106), (233, 147), (252, 159), (317, 200), (336, 212), (401, 253), (420, 265),
(485, 306), (504, 318), (569, 359), (970, 612), (1054, 665), (1455, 918), (1539,
971), (2108, 1330), (2593, 1636), (3162, 1995), (3647, 2301), (4216, 2660),
(4701, 2966), (5270, 3325), (5755, 3631), (6324, 3990), (6809, 4296), 7378,
4655), (7863, 4961), (8432, 5320), (8917, 5626), (9486, 5985), (9971, 6291),
(10540, 6650), (11025, 6956), (11594, 7315), (12079, 7621), (12648, 7980), ....
Except for (13, 8), (32, 20), (35, 22), and (54, 34), these are generalized
continued-fraction convergents of log(3)/log(2) (all the convergents except (1,
1), (2, 1), (3, 2), (4, 2), (6, 4), and (9, 6) are included).
The Minima in Collatz Cycles and Prime Gaps
In this section, c is restricted to being 1 or -1 and Halbeisen and
Hungerbühler's formula is used to compute the minimum in a cycle formed by a
limb in S of a least-residue tree attaching to itself at its beginning
(this assumes the cycle has the above parity vector).
l denotes the number of elements in the cycle and m denotes the
number of odd elements. The absolute value of 2l-3m
is not used when computing the "minimum". The minima where m is a multiple of a natural number d increase
and decrease in a regular fashion. For example, the truncated minima for
m=5, 10, 15, ..., 65 are 24, 24, 24, 24, 24, -19, -27, -35, -48, -70
-111, -219, and -1004 respectively, the truncated minima for m=70, 75,
80, ..., 130 are 463, 204, 137, 108, 88, -58, -70, -86, -111, -147, -219, -361,
and -1004 respectively, and the truncated minima for m=135, 140, 145,
..., 195 are 1561, 463, 281, 204, 162, 137, -111, -133, -165, -219, -295, -462,
and -1004 respectively. In general, the minima for d =5 have a
roughly saw-tooth shaped curve with a period of 13 or 14. Some long
periods (and large minima) occur for d=7, 12, 17, 19,
22, and 29; the periods are 10 or 11, 51 or 52, 17 or 18, 8 or 9, 7 or 8, and 27 or 28 respectively. The "superposition" of these
quasi-periodic "waves" is of importance in determining the largest minima.
For example, a large truncated minimum (for c=-1) of -3664765 occurs when
m=665=5∙7∙19.
The periods for prime m values less
than 41346 and of the
form 12k-1, k=1, 2, 3, ..., are 17, 24, 24, 18,
18, 22, 18, 15, 19, 19, ..., 17, 14, 16, 13, 13, 13, 16, 17, 15, and 13. A
period is considered to start with a negative minima value and end with a
positive minima value. A "peak" occurs when there is a positive spike in
minima values (at the end of a period) immediately followed by a negative spike. The difference in
m
values between successive peaks in minima values appears to be fairly constant
(usually 612, but as small as 528 or as large as 696).
Similar results apply for prime m values of the form 12k-5, 12k-7,
or 12k+1. Let x denote one-twelveth of the difference in
m values between successive peaks in minima values. For prime
m values less than 2000000, the x values range from 31 to 107, the
distribution of x values for 31, 32, 33, ..., 71 is 2, 5, 3, 11, 14, 22,
29, 29, 46, 98, 110, 156, 171, 228, 394, 418, 563, 697, 1047, 1578, 1561, 1367,
953, 819, 823, 477, 333, 270, 190, 175, 102, 70, 70, 40, 46, 24, 12, 10, 6, 9,
and 3 respectively
(a population centered around x=51), and the distribution of x
values for 91, 92, 93, ..., 107 is 1, 1, 0, 0, 0, 0, 1, 0, 3, 3, 3, 1, 3, 4, 3,
0, and 1 respectively (a second population centered around x=102). There should be infinitely many such populations. The minima appear to be
bounded for all m values in a given population. For example, 240∙1.5704 is
an upper bound of the minima (as computed using the m-cycle inequality)
in the first population when m is less than
1000000 and is still an upper bound of the minima in the first population when
m is less than 6000000. When c=-1, 239∙1.2002 is
an upper bound of the minima in the first population when m is less than
3000000 and is still an upper bound of the minima in the first population when
m is less than 6000000.
The minima in the second population do not increase monotonically within a
period; there is a characteristic dip about half-way through the period.
For example,
a graph of truncated upper bounds of minima (scaled by 32768.0) for m=609757, 609781,
609877, ..., 610993 (primes of the form 12k+1) is;

Similarly, there is a dip about a third of the way through the period and another dip
about two-thirds of the way through the period for the minima in the third population.
For example, a graph of truncated upper bounds of minima (scaled by 32768.0) for
m=5905433,
5905553, 5905673, ..., 5907353 (primes of the form 12k+5) is;

A graph of the maximum upper bounds of minima (scaled by 65536.0) for x
values from 31 to 72 (in the first population) for prime m values less
than 6000000 is;

(The scaled maximum upper bounds of minima for x=31, 32, 33, ..., 52 are
174, 188, 199, 226, 234, 248, 274, 295, 320, 344, 379, 418, 480, 532, 634, 746,
934, 1202, 1760, 3356, 24559, and 26346062 respectively. This appears to
be an exponential probability distribution where μ=1.1993e+06 with a 95%
confidence interval of (.8219e+06, 1.9136e+06). The scaled maximum upper
bounds of minima for x=53, 54, 55, ..., 72 appear to be random samples
from the same exponential probability distribution.) A graph
of the maximum upper bounds of minima (scaled by 65536.0) for x values
from 89 to 114 (in the second population) for prime m values less than
6000000 is;

A graph of the sorted maximum upper bounds of minima for x values from 89
to 144
for prime m values less than 6000000 is;

The periods for prime l values of the form 54k+1 are
approximately equal. Similar results apply for prime l values of
the form 54k+5, 54k+7, 54k+11, 54k+13, 54k+17,
54k+19, 54k+23, 54k+25, 54k+29, 54k+31, 54k+35,
54k+37, 54k+41, 54k+43, 54k+47, 54k+49, or 54k+53.
Let x denote one fifty-fourth of the difference in l values
between successive peaks in minima values. For prime l values less
than or equal to 3169919, the distribution of x values for 11, 12, 13,
..., 17 is 504, 1488, 2848, 4712, 4054, 1907, and 1009 respectively (a
population centered around x=14), the distribution of x values for
25, 26, 27, ..., 32 is 183, 937, 1510, 2826, 2409, 2020, 811, and 165
respectively (a population centered around x=28), the distribution of
x values for 40, 41, 42, ..., 46 is 433, 664,1312, 1258, 899, 705, and 184
respectively (a population centered around x=42), etc.
For prime l values less than or equal to 6339847, the scaled (by 65536.0)
maximum upper bounds of minima (as computed using the m-cycle inequality)
for x values of 11, 12, 13, ..., 17 are 6220270, 436632, 744405, 514414,
597, 256, and 166 respectively. For prime l values less than
or equal to 6339847, the scaled maximum upper bounds of minima for x
values of 25, 26, 27, ..., 32 are 332686, 1366582, 93783, 526748, 831, 299, 179,
and 130 respectively. For prime l values less than or equal to
6339847, the scaled maximum upper bounds of minima for x values of 40,
41, 42, ..., 46 are 301174, 540827, 101914, 1552, 362, 196, and 139
respectively. These appear to be exponential probability distributions.
For prime l values less than or equal to 9509761, the scaled maximum
upper bounds of minima for x values of 11, 12, 13, ..., 17 are 6220270,
436632, 744405, 916817, 900, 387, and 246 respectively. For prime l
values less than or equal to 9509761, the scaled maximum upper bounds of minima
for x values of 25, 26, 27, ..., 32 are 9037278, 1366582, 229310, 526748,
1320, 439, 269, and 195 respectively. For prime l values
less than or equal to 9509761, the scaled maximum upper bounds of minima for
x values of 40, 41, 42, ..., 46 are 301174, 540827, 149513, 2343, 521, 294,
and 204 respectively. In general, the scaled maximum upper bounds of
minima for the larger x values of each population are still growing.
(As the prime gaps become larger, the scaled maximum upper bounds of minima for
even the larger x values of say the first population should stop
growing.)
A graph of minima (along the y axis) for m=11, 59, 71, ..., 5099
(primes of the form 12k-1 where m+2 is also a prime)
is;

A graph of minima for
m=13, 61, 73, ..., 5101 (primes of the form 12k+1 where
m-2 is also a prime) is;

A graph of minima for
m=5, 17, 29, ..., 5021 (primes of the form 12k-7 where
m+2 is also a prime) is;

A graph of minima for
m=7, 19, 31, ..., 5023 (primes of the form 12k-5 where
m-2 is also a prime) is;

A graph of the upper bounds of the minima for
m=11, 59, 71, ..., 9767 (primes of the form 12k-1 where
m+2 is also a prime) is;

A graph of the upper bounds of the minima for
m=5, 17, 29, ..., 9929 (primes of the form 12k-7 where
m+2 is also a prime) is;

Tumbles and Jumps
In this section, c is restricted to being 1. Let y be an
even natural number such that y/2 is odd and denote [(y/2)(3/4)f]+1 where
f is a natural number and the
brackets denote the greatest integer function by v1. (The 3/4
factor corresponds to the "loss" due to a 2 in a sequence vector.)
v1
will be referred to as a "tumble" if it is odd (tumbles are the counterparts of
jumps). Usually, v1 is not in the 3n+1 sequence starting with
y/2. Under the same order constraints as least-residue trees, a succession
of tumbles and jumps (where the jumps start from the tumbles and the tumbles
start from the jumps) have properties similar to a live limb in S of
a least-residue tree. Denote the peaks and valleys in a succession of
tumbles and jumps by y/2, v1, p1,
v2, p2,
v3, p3, ..., vi, pi and denote the exponents of the
tumbles by f1, f2, f3, ...,
fi and
the exponents of the jumps by g1, g2, g3, ...,
gi.
The conditions to be imposed on y and the jumps are that y be less than the order (of the form 3∙2k) and greater than
order/2, each of p1, p2, p3,
..., pi be less than the order, and pi be greater than
order/3. These conditions do not always guarantee that v1
is in the 3n+1 sequence starting with y/2, v2 is
in the 3n+1 sequence
starting with p1, v3 is in the 3n+1 sequence starting with
p2, etc., but they come close to doing so. For example, for
i=2, f1=5,
g1=4, f2=5, g2=3, y=282825586, and an order of
402653184, v1=33557919, p1=169886969, v2=40314975,
and p2=136063043 where y, p1,
and p2 are within the specified bounds. The 3n+1
sequence starting with 141412793 (y/2) and having a length of 3f1+1 ends in
33557920, which is one larger than v1 (the 3 factor of the
tumble exponent corresponds to the number of elements in the 3n+1
sequence due to a 2 in a sequence vector) . The 3n+1 sequence
starting with 169886969 (p1) and having a length of 3f2+1
ends in 241889848, where [241889848/6]+1 equals v2. Denote the
natural numbers these 3n+1 sequences end in by j and k. Some possibilities for
different y values giving tumbles and jumps with exponents of 5, 4, 5,
and 3 respectively are; (1) v1=j and v2=k, (2)
v1=j-1
and v2=[k/6]+1, (3) v1=j-1 and
v2=[k/6], (4) v1=j
and v2=[k/6], (5) v1=[j/6]+1 and
v2=6k-5, (6)
v1=j-1 and v2=k-1, (7) v1=6j-5 and
v2=k,
(8) v1=[j/6]+1 and 3v2+1=[k/12], (9)
v1=[j/6]+1 and 3v2+1=[k/12]+1, and (10)
v1=j-1 and v2=36k-9
(there are other possibilities). In
general, if v1 is in the 3n+1 sequence starting with
y/2, there
are f1+1 odd natural numbers and 2f1 even natural numbers
in this sub-sequence (the same as for a sequence vector consisting of f1
2's), if v2 is in the 3n+1 sequence starting with
p1,
there are f2+1 odd natural numbers and 2f2 even natural
numbers in this sub-sequence (the same as for a sequence vector consisting of
f2 2's), if v3 is in the 3n+1 sequence starting with
p2, there are f3+1 odd natural numbers and 2f3 even
natural numbers in this sub-sequence (the same as for a sequence vector
consisting of f3 2's), etc. These limbs (not necessarily
1-2 sequence vectors) then have the same X
and Y values as a live limb in S of a least-residue tree.
References
(1) R. E. Crandall, On the "3x+1" Problem, Mathematics of
Computation, Vol. 32, No. 144, Oct. 1978, Pgs. 1281-1291.
(2) John H. Conway, Unpredictable Iterations, Proc. 1972 Number
Theory Conference, University of Colorado, Boulder, CO. 1972, pp. 49-52.
(3) Terras, R.,
A stopping time problem on the positive integers,
Acta Arithmetica
30 (1976), 241-252.
(4) Bohm, C., and Sontacchi, G., On the existence of cycles of
given length in integer sequences like xn+1=xn/2 if xn
even, and xn+1=3xn+1 otherwise,
Atti Accad. Naz. Lincei, VIII Ser., Rend., Cl. Sci. Fis. Mat. Nat. LXIV
(1978), 260-264.
(5) G. J. Wirsching, The Dynamical System Generated by the 3n+1
Function, 1681, Springer-Verlag (1998).
(6) L. Halbeisen and N. Hungerbühler, Optimal bounds for the length
of rational Collatz cycles, Acta Arith., LXXVIII.3, (1997), pgs. 227-239.
(7) R. P. Steiner, A theorem on the Syracuse problem,
Proceedings of the 7th Manitoba Conference on Numerical Mathematics and
Computation, 1977, pp. 553-559.
(8) J. L. Simons, On the Nonexistence of 2-cycles for the 3n+1 Problem,
Mathematics of Computation, Dec. 8, 2004, Vol. 74, No. 251, pgs. 1565-1572.
(9) J. Simons and B. de Weger, Theoretical and computational bounds for
m-cycles of the 3n+1 problem, Acta Arith. 2005.
(10) Edward G. Belaga [2003]: 21. "Effective
polynomial upper bounds to perigees and numbers of (3x + d)-cycles
of a given Oddlength", Acta Arithmetica 106, 197206.
(11) Georges Rhin, "Approximants de Padé et mesures effectives d'irrationalité",
Progress in Mathematics 71 [1987], 155-164.
(12) T. Brox, "Collatz cycles with few descents", Acta Arithmetica
92 [2000], 181-188.
(13) Hardy, G. H. and Littlewood, J. E., Some Problems of Diophantine
Approximation, Acta Math. 37 (1914), 193-239.
(14) Edward G. Belaga, Maurice Mignotte [2000]: "Cyclic
Structure of Dynamical Systems Associated with 3x+d Extensions of
Collatz Problem". U. Strasbourg report 2000-18, 57 pages.
http://hal.archives-ouvertes.fr/IRMA-ACF, file hal-00129656.
(15) Mihăilescu, P., Primary Cyclotomic Units and a Proof of Catalan's
Conjecture, J. Reine angew. Math. 572: 167-195.
Software
MSVC++™ C programs were used to confirm the above propositions. Readers
may copy and modify the software in this section. No guarantee is made
that it is error-free.
Use test0a to find cycles in the 3n+c sequence.
The "iters" variable specifies the number of jumps from the initial
n value in
the sequence (an odd natural number divisible by 3). Usually, "iters" is
set to 1. The list of cycles for c in the range from -151 to 151 was
generated using this setting. The list of cycles was confirmed to be the same
using an "iters" setting of 2 or 3. The cycles were verified to be the same as
those given by Keith Matthews' cycle-finding
program at "http://www.numbertheory.org/keith.html".
An improved cycle-finding program is test0azf (double-words are used).
A much faster cycle-finding program is test0azi.
Example output of this program (after some minor editing to fill in array sizes)
is c1. Another "include" file that is needed for
subsequent processing is ln. A program that does this
processing is test0cyu. Links to the
subroutines "euclid" and "halbhung" (and other required subroutines)
are given below. An output of this program is the (L, K)
values of the cycles with attachment points. A table of the (L,
K) values of the cycles with attachment points for c≤69997 is
newlk. A table of the (L, K) values
of the cycles with attachment points for 70001≤c≤99997 is
newlk1. A table of the (L, K)
values of the cycles with attachment points for 100001≤c≤149999 is
newlk2. A table of the (L, K)
values of the cycles with attachment points for 150001≤c≤199999 is
newlk3. These tables are "include" files for the
program test23r (which finds associated cycles).
The program test23s finds (L, K) trees.
A still faster cycle-finding program is test0azk.
TMS320C64™ assembly language subroutines used are jumps,
cycle, regen
and check.
These subroutines are usually at least an order of magnitude faster than corresponding C code (depending on
the compiler and microprocessor used for the C code). A program for finding cycles without attachment points is
test0azj. Other input to "test0cyu" is
c203, c401,
c601, c803, c1001,
c1201, c1403,
c1601, c1801,
c2003, c2201,
c2401, c2603,
c2801, c3001,
c3203, c3401,
c3601, c3803,
c4001, c4201,
c4403, c4601,
c4801, c5003,
c5201, c5401,
c5603, c5801,
c6001, c6203,
c6401, c6601,
c6803, c7001,
c7201, c7403,
c7601, c7801,
c8003, c8201,
c8401, c8603,
c8801, c9001,
c9203, c9401,
c9601, and c9803.
Attachment points for 3n+c cycles where c≤199999 are given
in att1, att2,
att3, att4, att5,
att6, att7,
att8, att9, att10,
att11, att12,
att13, att14, and
att15. Only one
attachment point per cycle is given and only the least significant word of the
attachment point is given. The program test0cyw
supplies the most significant word of the attachment point and regenerates the
other attachment points. Otherwise, this program does the same processing
as "test0cyu". A version of "test0cyw" where all the c
values up to 99997 can be processed at once is test0cyx.
"Include" files are att1t, att2t,
att3t, att4t, and
att5t.
Use test1c to histogram the |t2|-|t1|
values of 3n+c sequences starting with an odd integer divisible by 3 and
having a 1-2 sequence vector that attach to other such sequences.
Use test0b to regenerate a cycle in the 3n+c sequence
given an entry point (must be even) into the cycle. The order of the cycle
is computed. The output of "test0a" is input to this program.
Use test0c to regenerate cycles in the 3n+c sequence
given a list of entry points into the cycles. (The list of cycles is
confirmed.)
Use test0d to regenerate cycles in the 3n+c sequence
given a list of entry points into the cycles. A check for 1-2 sequence
vectors at entry points into the cycles is made (for "multiple jump" connection
points).
Use test0e to regenerate cycles in the 3n+c sequence
given a list of entry points into the cycles. A check for 1-2 sequence
vectors at entry points into the cycles is made (for "jumps over" connection
points).
list consists of the cycles found for c in the range from
-151 to 151.
list1 consists of one-attachment-point cycles found for
c
in the range from -151 to 151.
Use test1 to find the number of jumps in the 3n+1
sequence before an even natural number is reached (starting with an odd natural
number divisible by 3).
Use test2 to generate a histogram of limb lengths for a
3n+c sequence that is not an "odd" path. The
fourth-to-last element of the
sequence must be an odd natural number greater than order/6 and the
third-to-last element of the sequence must be an even natural number divisible
by 8. Use test2a to compute the (l, m)
values of generalized dead limbs. The "iters" variable is the number of
primary attachment points (usually, the "iters1" variable is set to the same
value). An updated version of this program is at
test2an.
Use test3a to generate limbs of least-residue trees
where at least one element of the limb is divisible by 8.
Use test3b to generate limbs of least-residue trees
where at least one element of the limb is divisible by 8. Multiple-word
arithmetic is used.
Use test3c to generate limbs of least-residue trees
where at least one element of the limb is divisible by 8. Multiple-word
arithmetic is used. This C program is for use on the TMS320C64™ digital
signal processing chip (with hand-optimized assembly language subroutines).
Use test4a12, test4a13,
test4a14, test4a15,
test4a16, test4a17,
test4a18, test4a19,
test4a20, test4a21,
test4a22, test4a23,
test4a24, test4a25,
test4a26, test4a27,
test4a28, test4a29,
test4a30, test4a31,
test4a32, and test4a33 to
compare the number of limbs in S of a given length to the estimated number of
limbs. Only live limbs are considered.
Use test5a to generate tumbles and jumps having three
peaks and two troughs.
Use test5b to generate tumbles and jumps having four
peaks and three troughs.
Use test6a to compute the largest y values, the
smallest y values, the largest z values, and the smallest z values for live limbs
in S
associated with a given sequence vector. The maximum |X(δ/y)| value is
computed.
Use test6b to compute the largest y values for live limbs
in S
associated with a given sequence vector. The maximum |X(δ/y)| value is
computed. This C program is for use on the TMS320C64™ digital signal
processing chip (with hand-optimized assembly language subroutines).
Use test7 to check that n(order/2)>ce,
c>0, n>0, or
(-n)(order/2)>(-c)e, n<0, c<0. Floating point arithmetic is used.
Use test8 to check that x>0 for limb lengths with
positive limits and x<0 for limb lengths with negative limits.
Use test9 to generate least-residue trees. The
permutation of A, B, C, and D for different c values is checked.
Use test10 to generate least-residue trees for the 3n-1
sequence, k≤15. Numerous properties of least-residue trees are tested.
Limbs in S having lengths of 5, 10, 15, 18, 23, and 28 are verified to be dead.
Use test11 to generate long limbs in S.
Sequence vectors are generated.
Use test12 to find sequence vectors corresponding to
different e values. All the orders up to 3∙224 are computed.
The maximum and minimum x/y values for live limbs are computed for every order
and are verified to be either ascending of descending.
Use test13 to compute a and b values.
Use test14a to compute the minimum element in a cycle
using the formula
Ml,m=∑(]jm/l[-](j-1)m/l[)2j-13m-]jm/l[
where the summation is from j=1 to l.
Use test14b to compute the minimum element in a cycle
in a limb of S of a least-residue tree. Use test14c to compute the minimum
element in a cycle in a limb of S of a least-residue tree (using the TMS320C64™
DSP.) Use test14d to
compute the minimum element in a cycle in a limb of S of a least-residue tree
when m and m+2 are primes. Use test14e
to output the computed minima for a cycle in a limb of S of a
least-residue tree. Use test14f to compute an
upper bound of the minimum element in a cycle in a limb of S of a
least-residue tree where m and m+2 are prime. Use
test14g to compute an upper bound of the minimum
element in a cycle in a limb of S of a least-residue tree when m is
prime. Use test14h to compute an upper bound of
the minimum element in a cycle in a limb of S of a least-residue tree when
m is prime (using the TMS320C64™ DSP). Use
test14i to generate the sequence vector corresponding to the smallest e
from the parity vector. Use test14j to
compute the largest odd element in a cycle using the floor function. Use
test14k to compute an upper bound of the minimum element
in a cycle in a limb of S of a least-residue tree when l is prime
(using the TMS320C64™ DSP).
Use test15 to generate parity vectors (distinct under
rotation) for given l and m values (using the TMS320C64™ DSP).
Subroutines called are bitcnt and
pack.
Use test16 to determine that the (l, m)
value of a generalized dead limb minus the (l, m) value of a
generalized continued-fraction convergent of log(3)/log(2) is the (l,
m) value of a shorter generalized dead limb.
Use test17
to show that |2l-3m| increases
monotonically when (l, m) are generalized continued-fraction
convergents of log(3)/log(2) (excluding (2,
1), (4, 2), (6, 4), and (9, 6)). |2l-3m|
is shown to increase monotonically for 105 generalized
continued-fraction convergents of log(3)/log(2).
This program is for use on the TMS320C64™ DSP.
Use test18
to generate the parity vector of a 3n+c cycle where twice the
minimum element in the cycle is larger than the maximum odd element in the cycle
(and the elements are large). This program is for use on the TMS320C64™
DSP. (A corresponding C program is test14uf.) sv gives a portion of this parity vector.
Use test14da to
compute Ml,m/(2l-3m)
values for the corresponding M-cycles.
Use test14db to determine if rotations of certain
parity vectors match the parity vector p.
Use test19 to
find rotations of the parity vector ]jm/l[
- ](j-1)m/l[, j=1, 2, 3, ..., l, where (0, 1,
0) is at the beginning of the vector and twice
the smallest s value is larger than the largest "odd" s value.
This program is for use on the TMS320C64™ DSP.
Use test19a to
find rotations of the vector satisfying the two additional conditions.
Use test20 to
find limbs in S almost having the parity vector ]jm/l[
- ](j-1)m/l[, j=1, 2, 3, ..., l (the parity
vector is rotated so that a (1, 1) is at the beginning of the vector and the
first 1 in the vector is changed to a 0 and the last element of the vector [a 0]
is changed to a 1). A subroutine used is limb.
This program is for use on the TMS320C64™ DSP.
test20a doesn't use the "limb" subroutine.
Use test21ca to compute the number of odd elements in
a one-jump (or multiple-jump) attachment point minus j where t≡u(mod
2j). test21cb computes these values for c values between 601 and 997.
test21cc computes these values for c values
between 1001 and 1499. test21cd computes these
values for c values between 1501 and 1999.
test21ce computes these values for c values between 2003 and 2497. Subroutines
used are halbhung and euclid. The properties of no-jump, one-jump, multiple-jump, and jumped-over
attachment points are tested.
Use log2 to compute the logarithm of 2.
Use log3o2 to compute the logarithm of 3/2.
Use expand to compute the generalized
continued-fraction convergents of log(3)/log(2). Use
test22 to compute the upper bound of the minimum in a 3n+c cycle using Proposition (43). Use
test23b
to factor Collatz numbers.
Multiple-word arithmetic C subroutines are add64, add128,
add256, add512, add1024,
carry, copy256,
copy512,
copy1024, div6432, div12864,
div25632, div102432,
div204832,
divn,
lshift256, lshift512, lshift1024, lmbd,
mul6432,
mul6464, mul12832, set256,
set512,
set1024, shift64,
shift128, shift256,
shift512,
shift1024, sub64, sub128,
sub256, sub512, sub1024,
subr2, n-word arithmetic,
table, table1,
table2, and table4.
Multiple-word arithmetic TMS320C64™ assembly language subroutines are
add64,
div12864, div6432,
mul6432,
mul6464,
mul3232,
shift64,
sub64, subr2, and
n-word arithmetic.
Other Topics
It's commonly known that there is a formula for Pythagorean triples (integer
solutions of a2+b2=c2).
It's less commonly known that there are "almost" integer solutions of a3+b3=c3.
When 3 does not divide a+b and a+b is factored out
of a3+b3, the equation a2-ab+b2=T3
is obtained and there are integer solutions of this equation. Solutions of
this equation are of interest since classical results from algebraic number
theory (Furtwängler's and Vandiver's theorems) are still applicable. This
topic is discussed in the link fermat.
In his book Elements of Algebraic Coding Theory (Chapman & Hall, 1996),
Lekh Vermani gives a proof of the quadratic reciprocity law using Perron's
theorem. Perron's theorem concerns the number of consecutive quadratic
residues and consecutive quadratic non-residues. Many textbooks on
algebraic number theory have sections on cubic, biquadratic, and octic
reciprocity. Whether a generalized version of Perron's theorem is still
applicable to higher-order reciprocity is discussed in the link
congr.
A relationship between the cross-ratio function of geometry and complex
analysis, the Poisson probability distribution, and Fermat's congruence modulo a prime power is discussed in the link
psquare.
Generalized Fibonacci and Lucas series are discussed in the link
nroots.
The cross-ratio function is discussed in the link cross.
The Farey series is discussed in the link farey.
The relationship between the Farey series and the Riemann hypothesis is
discussed in the link riemann.
A link to a 3n+c cycle C program with "include" files is
cycles.
























































































































































