
The 3n+1 Problem - Generalized Dead Limbs and Cycles with Attachment Points
© Darrell Cox, June 2020
Abstract: Generalized dead limbs are defined and used in conjunction with the continued-fraction convergents of log(3)/log(2) to analyze 3n+c cycles. Attachment points will be defined in the following. All the known 3n+c cycles with attachment points for |c|<53 have been verified to be in generalized dead limbs. This appears to be a necessary condition for 3n+c cycles with attachment points to exist. Most 3n+c cycles have attachment points and it appears that there is at least one 3n+c cycle with an attachment point for every |c| value.
The next element in a 3n+1 sequence is (3n+1)/2 if
n is odd, or n/2 otherwise. The more general 3n+c sequence
(where c is odd and not divisible by 3) is similarly defined. Consider a
3n+1 (or 3n-1) sequence (n>0) where the first element of
the sequence is initially an odd integer divisible by 3 and the last two
elements of the sequence are even (and the third-to-last element is odd). The order of this sequence is defined to be twice the smallest natural
number of the form 3∙2k greater than or equal to the element
in the sequence with the largest value. The sequence is then extended
backwards from the odd integer divisible by 3 until the order is exceeded. (The sequence is not extended
backwards to the point where it becomes equal to the order.) When the
second-to-last element of the sequence (possibly along with other elements of the
sequence) determines the order, these sequences will be referred to as
"generalized dead limbs" (named after limbs in the Collatz graph that can no
longer branch). This definition will be later amended to allow other
integers divisible by 4 to determine the order. For |c|>1, absolute values of sequence elements are
considered in determining the order. An example of a generalized dead limb
(for the 3n-1 sequence) is {336, 168, 84, 42, 21, 31, 46, 23,
34, 17, 25, 37, 55, 82, 41, 61, 91, 136, 68}. The order is 384.
Another example of a generalized dead limb (for the 3n-1 sequence) is
{246, 123, 184, 92, 46, 23, 34, 17, 25, 37, 55, 82, 41, 69, 91, 136, 68}.
The order is 384 and is determined by the sequence elements 184 and 136. Let e denote the number of
even elements in a generalized dead limb, m the number of odd elements,
and l the number of elements. An empirical
result is;
(1) For a given number of odd elements in a generalized dead limb where c=1
or -1 , the number of even elements is mostly fixed; the number of even
elements can deviate by at most 1. For example, for m=1, e can
equal 4 or 3. (The (e, m) value will be denoted by ((4,
3), 1).) (e, m) values for generalized dead limbs are ((4,
3), 1), ((5, 4), 2), ((5, 4), 3), ((6, 5), 4), ((6, 5), 5), ((7, 6), 6), ((8,
7), 7), ((8, 7), 8), ((9, 8), 9), ((9, 8), 10), ((10, 9), 11), ((11, 10), 12),
((11, 10), 13), ((12, 11), 14), ((12, 11), 15), ((13, 12), 16), ((13, 12), 17),
((14, 13), 18), ((15, 14), 19), ((15, 14), 20), ((16, 15), 21), (16, 15), 22),
((17, 16), 23), ((18, 17), 24), ((18, 17), 25), ((19, 18), 26), ((19, 18), 27),
(20, 19), 28), ((20, 19), 29), ((21, 20), 30), ((22, 21), 31), ((22, 21), 32),
((23, 22), 33), ((23, 22), 34), ((24, 23), 35), ((25, 24), 36), ....
This result will be generalized for |c|>1 after attachment points have been defined. In his 1978 article, Crandall1 proved a lower bound of 17985 for the number of odd elements in a 3n+1 cycle using the minimum in a hypothetical cycle and the continued-fraction convergents of log(3)/log(2). Recent 3n+1 cycle research frequently involves use of the continued-fraction convergents of log(3)/log(2). For some purposes, this is too restrictive; valuable information is thrown away. This is the rationale for defining generalized continued-fraction convergents (allowing less accurate approximations). Let (c, d), (e, f), and (g, h) denote successive continued-fraction convergents of a real number and let j denote the ceiling of h/f. (ei, fi) and (ei+c, fi+d), i=1, 2, 3, ..., j, can be considered to be generalized continued-fraction convergents of the real number. The generalized continued-fraction convergents of log(3)/log(2) are (1, 1), (2, 1), (3, 2), (4, 2), (5, 3), (6, 4), (8, 5), (9, 6), (11, 7), (16, 10), (19, 12), (24, 15), (27, 17), (38, 24), (46, 29), (57, 36), (65, 41), (76, 48), (84, 53), (130, 82), (149, 94), (168, 106), (233, 147), .... An empirical result is;
(2) The adjusted (l, m) values (where l is decremented by
4 or 3) of generalized dead limbs include the generalized continued-fraction convergents of log(3)/log(2).
Let K denote the number of odd elements in a 3n+c cycle and L
the number of even elements. Based on empirical evidence, the (K+L, K) value of a 3n+1 (or 3n-1) cycle is a generalized
continued-fraction convergent of log(3)/log(2). In 2004, Simons2 proved that if a nontrivial 2-cycle exists, then (K+L,
K) must be a convergent in the continued-fraction expansion of log2
3. Let δ denote log(3)/log(2). Using an empirically derived lower bound for the minimum element in an m-cycle,
Simons and de Weger3 proved that δK<K+L<1.000001δK.
Assuming the factor of 1.000001 in Simons and de Weger's inequality can be
reduced to 1.0, the (K+L, K) value of a 3n+1 cycle
is a continued-fraction convergent of log(3)/log(2). The (K+L, K)
value of the 3n+1 cycle {2, 1} is (2,1). The (K+L,
K) value of the 3n-1 cycle {1) is (1, 1). The (K+L,
K) value of the 3n-1 cycle {5, 7, 10} is (3, 2). The (K+L,
K) value of the 3n-1 cycle {34, 17, 25, 37, 55, 82, 41, 61, 91,
136, 68} is (11, 7)
and the (l, m) value of the extended sequence {336, 168, 84,
..., 68} (a generalized dead limb containing the cycle) is (19, 10). An
empirical result is;
(3) The ((l+1, l), m) value of a generalized dead limb
plus the (e,
f) value of a generalized continued-fraction convergent of log(3)/log(2)
is the ((l'+1, l'), m') value of another generalized dead limb.
For example, for the generalized continued-fraction convergent (3, 2), l+1+3
is equal to or one less than l' +1 and m+2 is equal to m'.
In the case where l+1+3 is one less than l'+1, l+1+3
is still equal to l'. For the generalized continued-fraction
convergent (16, 10), l+1+16 is equal to or one greater than l'+1
and m+10 is equal to m'. In the case where l+1+16 is
one greater than l'+1, l+16 is still equal to l'+1.
In general, ((l+1, l), m) plus (e, f) equals
((l'+1, l), m') (in the above sense).
When a generalized dead limb contains a cycle, let (l', m') denote the length and number of odd elements of the portion of the generalized dead not in the cycle. Let e' denote the number of even elements. For the c=-1 cycles, (l', m')=(8, 3) and (6, 2). An empirical result based on this is, the assumption that the (K+L, K) values of c=1 or -1 cycles are generalized continued-fraction convergents of log(3)/log(2), and Proposition (3) is;
(4) When c=1 or -1, the e' values are mostly fixed. The deviations are the same as in Proposition (1).
Attachment points in a 3n+c cycle are defined to be even integers i such that i-c is divisible by 3 (and (i-c)/3 is not already in the cycle). An attachment point i will be said to be primary if 4i is not an attachment point. If i is a primary attachment point and 4 divides i, then i/4 will be said to be the secondary attachment point, etc. In the cycle for c=-1, 68 is the only attachment point. (There are no attachment points in the other known 3n+1 or 3n-1 cycles.) In the following, 3n+c sequences are extended backwards from attachment points. "Odd" paths are taken, that is, if i is an even integer in the extended sequence and 3 divides i-c, then the path (i-c)/3 (and not 2i) is taken. Presumably, an odd integer divisible by 3 (denoted by t) will be reached. The t value of a primary attachment point will be said to be the "proxy" of the first odd element in the cycle after the preceding primary attachment point (in the case where there is only one primary attachment point, the preceding primary attachment point is the primary attachment point). (Note that the sequence vector of the cycle elements starting with the first odd element after the preceding primary attachment point and ending with the primary attachment point is a 0-1 sequence vector; this is the motivation for taking "odd" paths when extending sequences backwards from attachment points. For the c=-1 cycle, t equals 21 and is the proxy of the cycle element 17.) The definition of attachment points for generalized dead limbs is similar; the attachment points are just not necessarily in cycles (and the sequence initially starts with an odd integer divisible by 3).
Generalized Dead Limbs for c=5, 7, 11, and Other Cycles
There are four known 3n+5 cycles with attachment points. One such cycle is {1, 4, 2}. The (K+L, K) value of the cycle is (3, 1). A generalized dead limb (with one primary attachment point [2]) containing the cycle is {-6, -3, -2, -1, 1, 4, 2}. The order is 12 and (l, m)=(7, 3), a value consistent with Proposition (1). Also, (l', m')=(4, 2), a value not consistent with Proposition (4). Apparently, there are no generalized dead limbs with two or more primary attachment points that contain the cycle.
Another cycle is {19, 31, 49, 76, 38}. The (K+L, K) of this cycle is (5, 3), a generalized continued-fraction convergent of log(3)/log(2). The cycle has one attachment point (38). A generalized dead limb with one primary attachment point (38) containing the cycle is {96, 48, 24, 12, 6, 3, 7, 13, 22, 11, 19, 31, 49, 76, 38}. The order is 192 and (l, m)=(15, 7), a value consistent with Proposition (1). Also, (l', m')=(10, 4), a value consistent with Proposition (4). Another generalized dead limb with two primary attachment points (26 and 38) containing the cycle is {132, 66, 33, 52, 26, 13, 22, 11, 19, 31, 49, 78, 38}. The order is 192 and (l, m)=(13, 6), a value consistent with Proposition (1). Also, (l', m')=(8, 3), a value consistent with Proposition (4). Another generalized dead limb with two primary attachment points (44 and 38) containing the cycle is {114, 57, 88, 44, 22, 11, 19, 31, 49, 76, 38}. The order is 192 and (l, m)=(11, 5), a value consistent with Proposition (1). Also, (l', m')=(6, 2), a value consistent with Proposition (4). Another generalized dead limb with two primary attachment points (14 and 38) containing the cycle is {168, 84, 42, 21, 34, 17, 28, 14, 7, 13, 22, 11, 19, 31, 49, 76, 38}. The order is 192 and (l, m)=(17, 8). Also, (l', m')=(12, 5). Another degree of freedom is possible in this generalized dead limb. The corresponding (e, m) value is ((9, 8, 7), 8) and the corresponding (e', m') value is ((7, 6, 5), 5). Apparently, there are no generalized dead limbs with three or more primary attachment points that contain the cycle.
Another cycle is {781, 1174, 587, 883, 1327, 1993, 2992, 1496, 748, 374, 187, 283, 427, 643, 967, 1453, 2182, 1091, 1639, 2461, 3694, 1847, 2773, 4162, 2081, 3124, 1562} The (K+L, K) value of this cycle is (27, 17) ( a generalized continued-fraction convergent of log(3)/log(2)). The cycle has two primary attachment points (1562 and 1496) and one secondary attachment point (374). A generalized dead limb with two primary attachment points containing the cycle is {8304, 4152, 2076, 1038, 519, 781, 1174, 587, 883, 1327, 1993, 2992, 1496, 748, 374, 187, 283, 427, 643, 967, 1453, 2182, 1091, 1639, 2461, 3694, 1847, 2773, 4162, 2081, 3124, 1562}. The order is 12288 and (l, m)=(32, 18), a value consistent with Proposition (1). Also, (l', m')=(5, 1), a value consistent with Proposition (4). There are thirteen generalized dead limbs having fewer than four primary attachment points that end in the cycle attachment point 1562 (and thus contain parts of the cycle). The corresponding (l, m) values are (24, 13), (16, 8), (26, 14), (18, 9), (19, 10), (21, 11), (23, 12), (29, 16), (27, 15), (30, 13), (27, 15), (30, 17), and (34, 19). All these values are consistent with Proposition (1). There is one generalized dead limb having fewer than four primary attachment points that ends in the cycle attachment point 1496. The corresponding (l, m) value is (12, 6, ), a value consistent with Proposition (1). Apparently, there are no generalized dead limbs with four or more primary attachments points that contain the cycle or any portion of it.
The remaining cycle is {359, 541, 814, 407, 613, 922, 461, 694, 347, 523, 787, 1183, 1777, 2668, 1334, 667, 1003, 1507, 2263, 3397, 5098, 2549, 3826, 1913, 2872, 1436}. The (K+L, K) of this cycle is (27, 17), the same as the above cycle. (Such cycles are generated from permutations of parity vectors having the same number of 1's and 0's and will be said to be "interrelated". Some of these permutations may not have attachment points.) The cycle has two primary attachment points (1436 and 1334). There doesn't appear to be a generalized dead limb that contains the entire cycle. There are five generalized dead limbs having fewer than three primary attachment points that end in the cycle attachment point 1334. The corresponding (l, m) values are (20, 11), (12, 6), (15, 8), (19, 10), and (23, 13). All these values are consistent with Proposition (1). Apparently, there are no generalized dead limbs with three or more primary attachment points that contain the cycle or any portion of it.
There is one known 3n+7 cycle with an attachment point. The cycle is {5, 11, 20, 10} and (K+L, K)=(4, 2), a generalized continued-fraction convergent of log(3)/log(2). A generalized dead limb with one primary attachment point (10) containing the cycle is {-24, -12, -6, -3, -1, 2, 1, 5, 11, 20, 10}. The order is 48 and the (l, m) value is (11, 5), a value consistent with Proposition (1). Also, (l', m')=(7, 3), a value consistent with Proposition (4). A generalized dead limb with two primary attachment points (4 and 10) containing the cycle is {24, 12, 6, 3, 8, 4, 2, 1, 5, 11, 20, 10}. The order is 48 and the (l, m) value is (12, 4). Also, (l', m')=(8, 2). Another degree of freedom is possible in this generalized dead limb. The corresponding (e, m) value is ((8, 6, 5), 4) and the corresponding (e', m') value is ((6, 5, 4), 2). Apparently, there are no generalized dead limbs with three or more primary attachment points that contain the cycle or any portion of it.
There are two known 3n+11 cycles with attachment points. One such cycle is {4, 2, 1, 7, 16, 8}. The (K+L, K) value is (6, 2), a value consistent with Proposition (1). The cycle has a primary attachment point (8) and a secondary attachment point (2). A generalized dead limb with three primary attachment points (-4, 2, and 8) containing the cycle is {-36, -18, -9, -8, -4, -2, -1, 4, 2, 1, 7, 16, 8}. The order is 48 and (l, m)=(13, 4). Another degree of freedom is possible in this generalized dead limb. The corresponding (e, m) value is ((9, 6, 5), 4). Also (l', m')=(7, 2), a value consistent with Proposition (4). Another generalized dead limb with three primary attachment points (-10, 2, and 8) containing the cycle is {-30, -15, -17, -20, -10, -5, -2, -1, 4, 2, 1, 7, 16, 8}. The order is 48 and (l, m)=(8, 4). Also (l', m')=(8, 4). Another degree of freedom is possible in this generalized dead limb. The corresponding (e, m) and (e', m') values are ((6, 5, 4), 4). A generalized dead limb with one primary attachment point (8) containing part of the cycle is {-24, -12, -6, -3, 1, 7, 16, 8}. The order is 48 and (l, m)=(8, 3), a value consistent with Proposition (1). Apparently, there are no generalized dead limbs with four or more primary attachment points that contain the cycle or any portion of it.
The other cycle is {31, 52, 26, 13, 25, 43, 70, 35, 58, 29, 49, 79, 124, 62}. The (K+L, K) value is (14, 8). The cycle has two attachment points (62 and 26). A generalized dead limb with two primary attachment points (62 and 26) containing the cycle is (288, 144, 72, 36, 18, 9, 19, 34, 17, 31, 52, 26, 13, 25, 43, 70, 35, 58, 29, 49, 79, 124, 62}. The order is 384 and (l, m)=(23, 11). Also, (l', m')=(9, 3). Another degree of freedom is possible in this generalized dead limb. The corresponding (e, m) value is ((12, 10, 9), 11) and the corresponding (e', m') value is ((6, 5, 4), 3). A generalized dead limb with three primary attachment points (68, 62, and 26) containing the cycle is {348, 174, 87, 136, 68, 34, 17, 31, 52, 26, 13, 25, 43, 70, 35, 58, 29, 49, 79, 124, 62}. The order is 384 and (l, m)=(21, 10). Another degree of freedom is possible in this generalized dead limb. The corresponding (e, m) value is ((11, 9, 8), 10). Also, (l', m')=(7, 2), a value consistent with Proposition (4). Another generalized dead limb with three primary attachment points (38, 26, and 62) containing the cycle is {300, 150, 75, 118, 59, 94, 47, 76, 38, 19, 34, 17, 31, 52, 26, 13, 25, 43, 70, 35, 58, 29, 49, 79, 124, 62}. The order is 384 and (l, m)=(26, 13). Also, (l', m')=(12, 5). Another degree of freedom is possible in this generalized dead limb. The corresponding (e, m) value is ((13, 11, 10), 13) and the corresponding (e', m') value is ((7, 6, 5), 5). There are four generalized dead limbs with fewer than four primary attachment points that end in the cycle attachment point 62 but do not include the entire cycle. The corresponding (l, m) values are (20, 9), (13, 6), (15, 7), and (21, 10). Only the generalized dead limbs with (l, m) values of (13, 6) and (15, 7) have two degrees of freedom. There is one generalized dead limb with fewer than four primary attachment points that end in the cycle attachment point 26. The (l, m) value is (11, 4). This generalized dead limb has another degree of freedom. Apparently, there are no generalized dead limbs with four or more primary attachment points that contain the cycle or any portion of it.
Generalized dead limbs do not contain the c=-23 cycles {4718, 2359, 3527, 5279, 7907, 11849, 17762, 8881, 13310, 6655, 9971, 14945, 22406, 11203, 16793, 25178, 12589, 18872, 9436} and {4526, 2263, 3383, 5063, 7583, 11363, 17033, 25538, 12769, 19142, 9571, 14345, 21506, 10753, 16118, 8059, 12077, 18104, 9052}. A generalized dead limb does not contain the c=25 cycle {44, 22, 11, 29, 56, 28, 14, 7, 23, 47, 83, 137, 218, 109, 176, 88}. A generalized dead limb does not appear to contain the c=29 cycle {4, 2, 1, 16, 8}. A generalized dead limb does not contain the c=37 cycle {23, 53, 98, 49, 92, 46}. The c=-23 cycles and the c=37 cycle have one attachment point. The c=25 cycle has three primary attachment points (22 is considered to be a primary attachment point because it precedes 88). The c=29 cycle has two primary attachment points (2 is considered to be a primary attachment point because it precedes 8).
A Modified Definition of Generalized Dead Limbs
In the modified definition, the primary attachment point with the largest absolute value is used in computing the order. This appears to allow infinitely many generalized dead limbs that contain a particular cycle.
In the above cycles that are not contained in a generalized dead limb, the cycles are contained in a newly-defined generalized dead limb with one more primary attachment point than the primary cycle attachment points. A generalized dead limb containing the c=5 cycle is {20412, 10206, 5103, 7657, 11488, 4755, 2872, 1436, 718, 359, 541, 814, 407, 613, 922, 461, 694, 347, 523, 787, 1183, 1777, 2668, 1334, 667, 1003, 1507, 2263, 3397, 5098, 2549, 3826, 1913, 2872, 1436}. The order is 24576 and (l, m)=(35, 19). A generalized dead limb containing one of the c=-23 cycles is {179064, 89532, 44766, 22383, 33563, 50333, 75488, 37744, 18872, 9436, 4718, 2359, 3527, 5279, 7907, 11849, 17762, 8881, 13310, 6655, 9971, 14945, 22406, 11203, 16793, 25178, 12589, 18871, 9436}. The order is 196608 and (l, m)=(29, 15). A generalized dead limb containing the other c=-23 cycle is {172140, 86070, 43035, 64541, 96800, 48400, 24200, 12100, 6050, 3025, 4526, 2263, 3383, 5063, 7583, 11363, 17033, 25538, 12769, 19142, 9571, 14345, 20506, 10753, 16118, 8059, 12077, 18104, 9052}. The order is 196608 and (l, m)=(29, 15). A generalized dead limb containing the c=25 cycle is {1176, 588, 294, 147, 233, 362, 181, 284, 142, 71, 119, 191, 299, 461, 704, 352, 176, 88, 44, 22, 11, 29, 56, 28, 14, 7, 23, 47, 83, 137, 218, 109, 176, 88}. The order is 1536 and (l, m)=(34, 16). A generalized dead limb containing the c=29 cycle is {29082, 14541, 21826, 10913, 16384, 8192, 4096, 2048, 1024, 512, 256, 128, 64, 32, 16, 8, 4, 2, 1, 16, 8}. The order is 49152 and (l, m)=(21, 3). A generalized dead limb containing the c=37 cycle is {720, 360, 180, 90, 45, 86, 43, 83, 143, 233, 368, 184, 92, 46, 23, 53, 98, 49, 92, 46}. The order is 768 and (l, m)=(20, 8). Some of these (l, m) values differ substantially from those given in Proposition (1).
Weibull Probability Distributions and Generalized Dead Limbs
Degrees of freedom in the (e, m) values are still relevant in this new definition of generalized dead limbs. The (e, m) values in generalized dead limbs having a certain number of primary attachment points and a certain number of odd elements are more easily modeled statistically than others. This statistical model appears to be about the same for all c values. This appears to be the case even when the (e, m) values can't be modeled with a known probability distribution.
In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((18, 17), 24). For c=1, odd integers divisible by 3 less than or equal to 99999999, five primary attachment points, and m =24, the (e, m) value, e>18, is ((19, 20, 21, ..., 44), 24). The respective numbers of values are 32797, 47787, 59588, 64148, 62252, 54381, 44726, 34653, 25588, 17468, 12348, 8024, 5036, 3415, 2201, 1398, 925, 455, 288, 167, 80, 42, 13, 1, 3, and 1. The sample size is 477785. Weibull probability distributions are used to model birth and decay processes and have a scaling and shaping parameter. For a Weibull probability fit of the data, the scaling parameter is 6.2179 with a 95% confidence interval of (6.2078, 6.2280) and the shaping parameter is 1.8463 with a 95% confidence interval of (1.8423, 1.8503). A histogram of the data with the corresponding Weibull probability distribution is;

The peak of the histogram is slightly larger than predicted. For c=-1, odd integers divisible by 3 less than or equal to 99999999, five primary attachment points, and m =24, the (e, m) value, e>18, is ((19, 20, 21, ..., 43), 24). The respective numbers of values are 32471, 48272, 59419, 64490, 61853, 54531, 44851, 33718, 25043, 17662, 12106, 8289, 5447, 3113, 1946, 1198, 656, 415, 258, 162, 74, 36, 7, 3, and 2. The sample size is 476022 (almost the same as for c=1). For a Weibull probability fit of the data, the scaling parameter is 6.1924 with a 95% confidence interval of (6.1824, 6.2024) and the shaping parameter is 1.8555 with a 95% confidence interval of (1.8515, 1.8596). A histogram of the data with the corresponding Weibull probability distribution is;
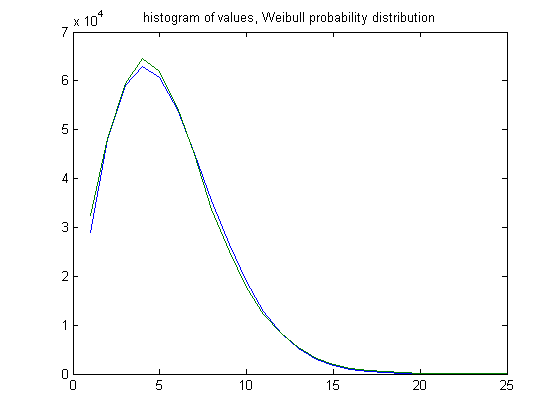
The peak of the histogram is slightly larger than predicted. For c=5, odd integers divisible by 3 less than or equal to 99999999, five primary attachment points, and m =24, the (e, m) value, e>18, is ((19, 20, 21, ..., 48), 24). The respective numbers of values are 25996, 38169, 47566, 51541, 49987, 43435, 35544, 27358, 20141, 14444, 9901, 6353, 4143, 2676, 1871, 1133, 725, 424, 201, 116, 47, 27, 6, 2, 5, 4, 2, 1, 0, and 1. The sample size is 381819. For a Weibull probability fit of the data, the scaling parameter is 6.2234 with a 95% confidence interval of (6.2121, 6.2346) and the shaping parameter is 1.8462 with a 95% confidence interval of (1.8417, 1.8507). A histogram of the data with the corresponding Weibull probability distribution is;
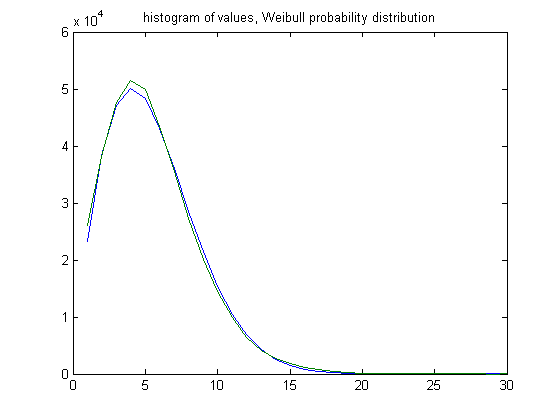
The peak of the histogram is slightly larger than predicted. For c=7, odd integers divisible by 3 less than or equal to 99999999, five primary attachment points, and m =24, the (e, m) value, e>18, is ((19, 20, 21, ..., 48), 24). The respective numbers of values are 27956, 41081, 51324, 55393, 53061, 46723, 38211, 29401, 22046, 15223, 10349, 7091, 4457, 2820, 1784, 1060, 611, 380, 249, 122, 78, 40, 22, 13, 2, 0, 0, 0, 0, and 1. The sample size is 409498. For a Weibull probability fit of the data, the scaling parameter is 6.2068 with a 95% confidence interval of (6.1960, 6.2176) and the shaping parameter is 1.8512 with a 95% confidence interval of (1.8469, 1.8556). A histogram of the data with the corresponding Weibull probability distribution is;
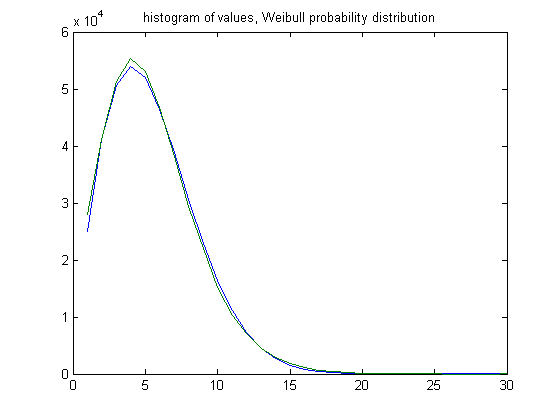
The peak of the histogram is slightly larger than predicted. For c=461, odd integers divisible by 3 less than or equal to 99999999, five primary attachment points, and m =24, the (e, m) value, e>18, is ((19, 20, 21, ..., 48), 24). The respective numbers of values are 32793, 48219, 59572, 63888, 61437, 53879, 44536, 34178, 25208, 17810, 12221, 8268, 5144, 3194, 1980, 1248, 740, 439, 219, 132, 76, 36, 25, 9, 7, 6, 4, 1, 0, and 1. The sample size is 475270. For a Weibull probability fit of the data, the scaling parameter is 6.1961 with a 95% confidence interval of (6.1861, 6.2062) and the shaping parameter is 1.8491 with a 95% confidence interval of (1.8450, 1.8531). A histogram of the data with the corresponding Weibull probability distribution is;
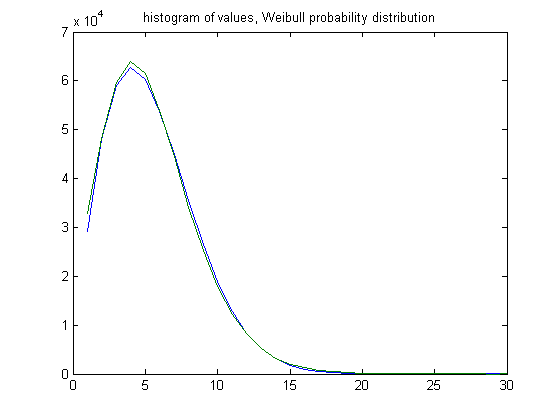
The peak of the histogram is slightly larger than predicted. Although the sample sizes differ considerably, the Weibull scaling and shaping parameters are about the same.
Sample Sizes
A plot of all the sample sizes (for m=5 to 93) for generalized dead limbs with five primary attachment points and for c=1 is;
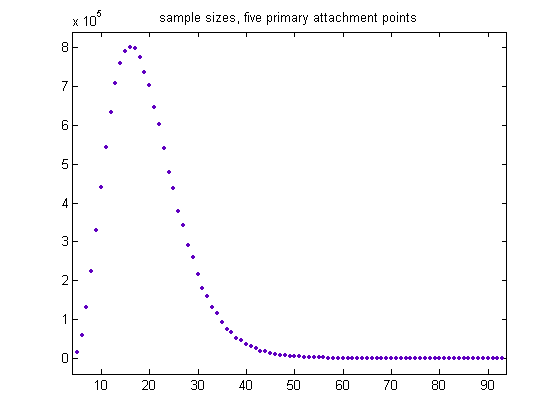
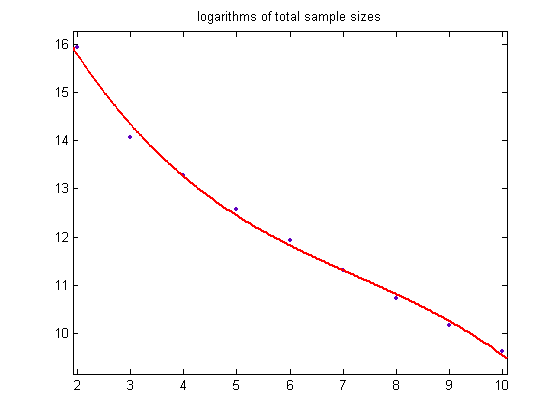
The total sample size is 13744792, the mean is 19.3956, and the standard deviation is 7.4143. Except for the long right-hand tail, the distribution resembles a normal probability distribution. The sample size should then decrease exponentially as m increases. For a cubic least-squares fit of the logarithms of the sample sizes starting with the largest (800237), p1=3.403e-5 with a 95% confidence interval of (2.588e-5, 4.219e-5), p2=-0.006312 with a 95% confidence interval of (-0.007609, -0.005016), p3=0.1433 with a 95% confidence interval of (0.08001, 0.2065), p4=12.78 with a 95% confidence interval of (11.86, 13.71), SSE=5.289, R-squared=0.9964, and RMSE=0.2769. A plot of the data is;
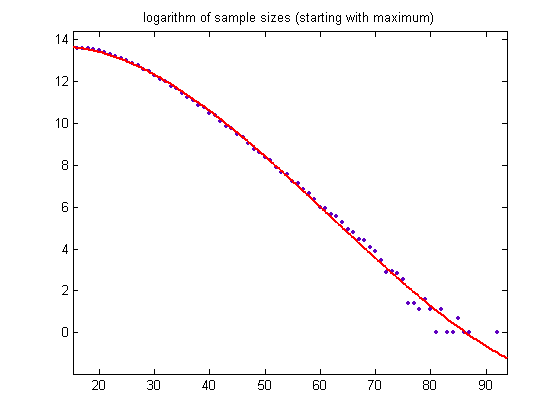
(Logarithms of 0 zero are set to 0.) For the corresponding cubic least-squares fit where the upper bound of the odd integers divisible by 3 is 39999999, the coefficients are 3.289e-5 with a 95% confidence interval of (2.351e-5, 4.227e-5), -0.004497 with a 95% confidence interval of (-0.005513, -0.003481), -0.03444 with a 95% confidence interval of (-0.06571, -0.003158), and 12.78 with a 95% confidence interval of (12.52, 13.04). At least the first and last coefficients match fairly well. A plot of the values is;
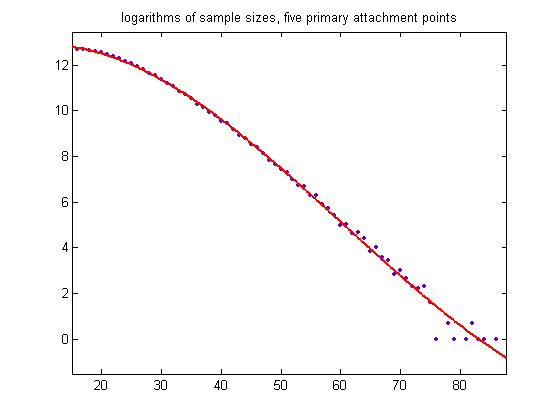
For a larger upper bound of odd integers divisible by 3 (larger than 99999999), the m values where the sample sizes become zero can be predicted to some extent. For these values, the alternative is for the (e, m) values to be consistent with Proposition (1).
A plot of the sample sizes for generalized dead limbs with two primary attachment points (and for c=1) is;
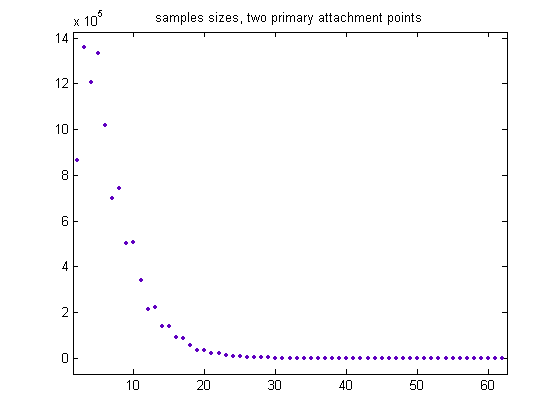
The total sample size is 9701505, the mean is 6.688307, and the standard deviation is 4.1389. A plot of the sample sizes for generalized dead limbs with three primary attachment points is;
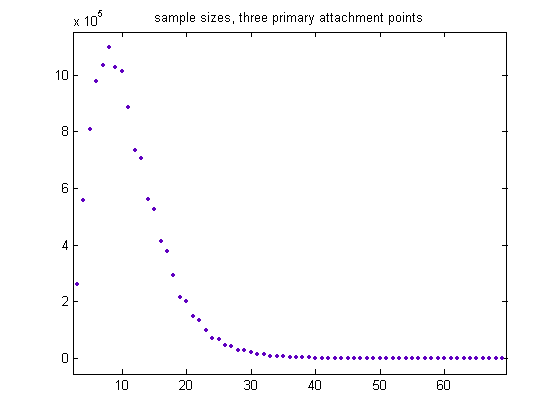
The total sample size is 12432051, the mean is 10.9867, and the standard deviation is 5.4324. A plot of the sample sizes for generalized dead limbs having four primary attachment point is;
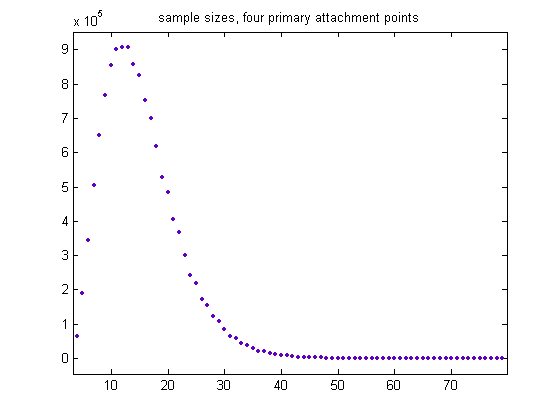
The total sample size is 13366566, the mean is 15.2322, and the standard deviation is 6.4921. A plot of the sample sizes for generalized dead limbs having six primary attachment points is;
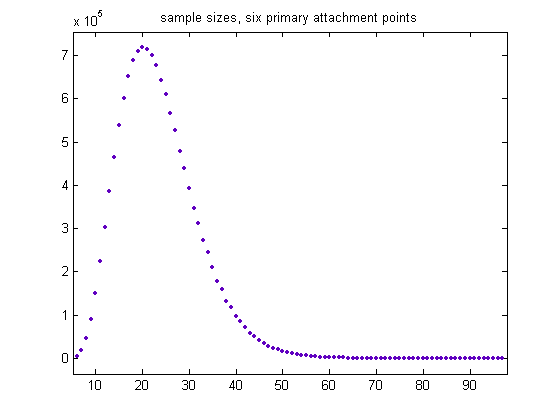
The total sample size is 13912770, the mean is 23.5093, and the standard deviation is 8.2373. A plot of the sample sizes for generalized dead limbs having seven primary attachment points is;
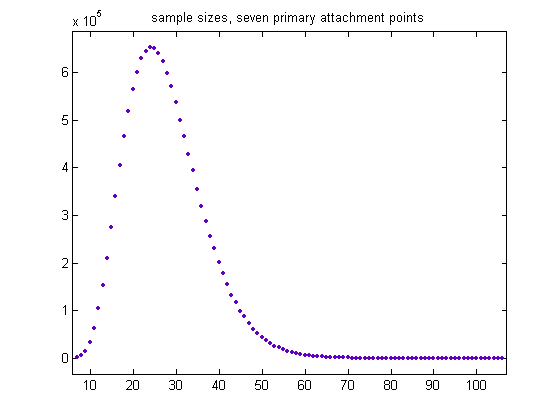
The total sample size is 13967262, the mean is 27.6091, and the standard deviation is 8.9883. A plot of the sample sizes for generalized dead limbs having eight primary attachment point is;
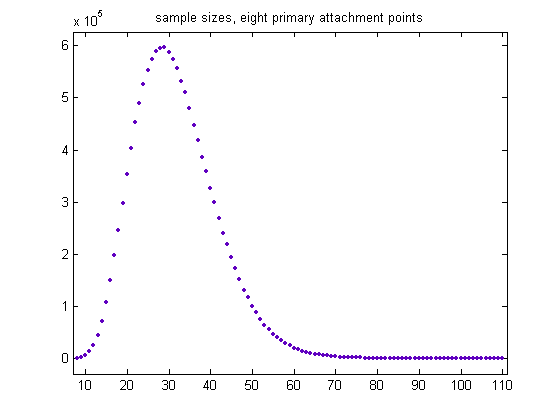
The total sample size is 13925644, the mean is 31.7470, and the standard deviation is 9.6984. A plot of the sample sizes for generalized dead limbs having nine primary attachment points is;
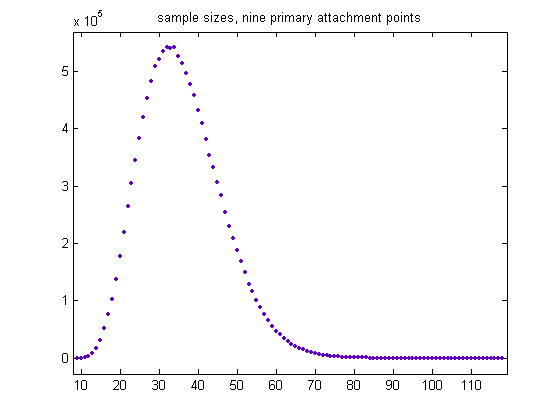
The total sample size is 13765108, the mean is 35.9817, and the standard deviation is 10.3850. A plot of the sample sizes for generalized dead limbs having ten primary attachment points is;
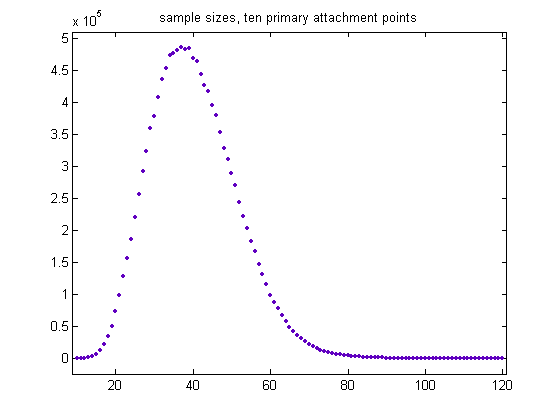
The total sample size is 13443046, the mean is 40.3589, and the standard deviation is 11.0463. For a cubic least-squares fit of the logarithms of the sample sizes starting with the largest (485751), p1=6.802e-6 with a 95% confidence interval of (2.479e-6, 1.113e-5), p2=-0.002831 with a 95% confidence interval of (-0.003847, -0.001815), p3=0.1456 with a 95% confidence interval of (0.06981, 0.2214), p4=11.42 with a 95% confidence interval of (9.635, 13.2), SSE=3.604, R-squared=0.9973, and RMSE=0.2136. A plot of the data is;

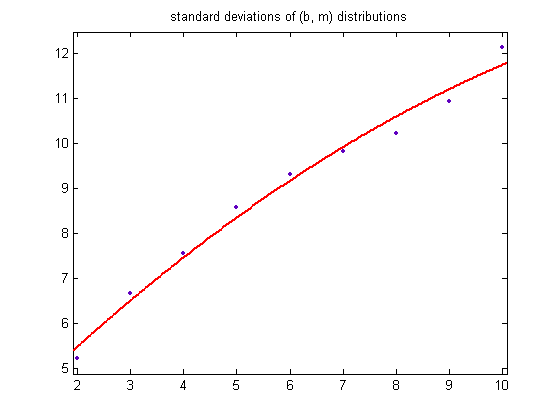
For a linear least-squares fit of the above means, p1=4.182 with a 95% confidence interval of (4.153, 4.211), p2=-1.591 with a 95% confidence interval of (-0.517, 0.09584), SSE=0.0643, R-squared=0.9999, and RMSE=0.09584. A plot of the data is;
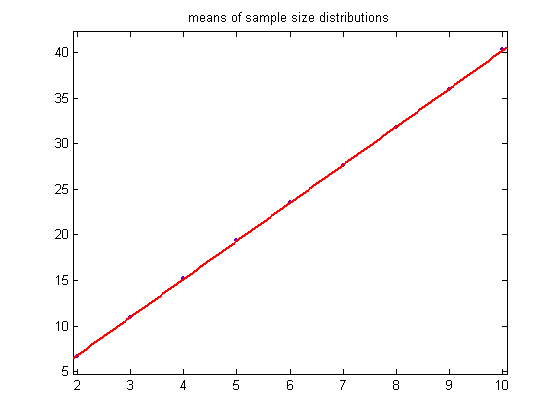
For a quadratic least-squares fit of the above standard deviations, p1=-0.04027 with a 95% confidence interval of (-0.0517, -0.02884), p2=1.324 with a 95% confidence interval of (1.185, 1.464), p3=1.753 with a 95% confidence interval of (1.377, 2.128), SSE=0.04032, R-squared=0.9991, and RMSE=0.08197). A plot of the data is;

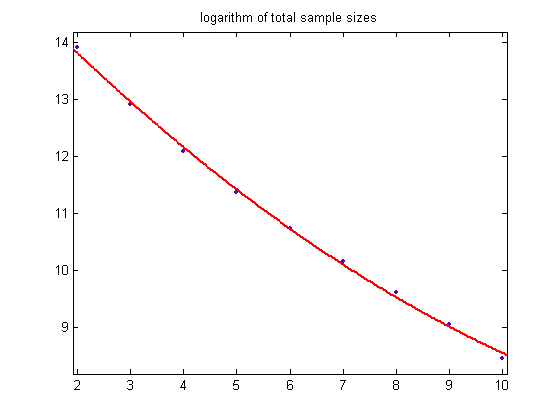
A plot of the total sample sizes is;
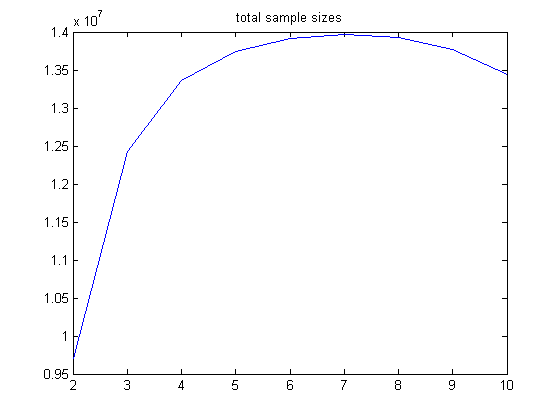
The means are larger and the standard deviations smaller for a smaller upper bound of odd integers divisible by 3. For odd integers divisible by 3 less than or equal to 39999999, the means of the sample sizes are 7.1321, 13.218386, 18.261716, 23.1206, 27.8792, 32.5848, 37.2942, 42.6792, and 48.0810 and the standard deviations are 4.0511, 4.8581, 5.5736, 6.1939, 6.74129, 7.2288, 7.6812, 7.9295, and 8.1189 (for generalized dead limbs with 2, 3, 4, ..., 10 primary attachment points). The means increase linearly and the standard deviations quadratically (although the coefficients in the least-squares fits are different). The corresponding total sample sizes are 3437751, 3481184, 3621628, 3637071, 3610635, 3571015, 3526628, 3271628, and 3046781.
The largest m values of the above distributions are 61, 68, 78, 92, 96, 106, 109, 117, and 119 (excluding values greater than 120). For a quadratic least-squares fit of these values, p1=-0.4838 with a 95% confidence interval of (-0.7928, -0.1746), p2=13.39 with a 95% confidence interval of (9.613, 17.16), p3=34.31 with a 95% confidence interval of (24.15, 44.47), SSE=29.5, R-squared=0.9917, and RMSE=2.217. A plot of these values is;
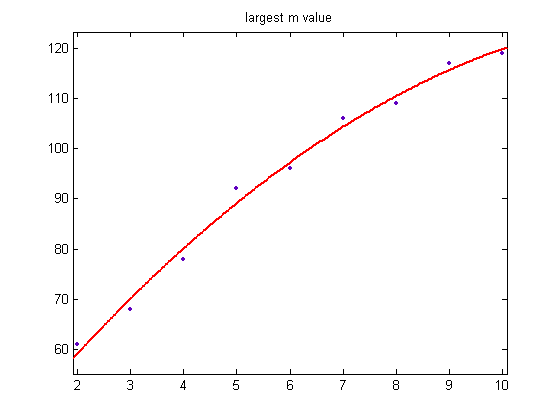
Values greater than 120 are excluded because the (e, m) values in Proposition (1) haven't been determined for m>120. For the generalized dead limbs with nine primary attachment points, there is a generalized dead limb with 129 odd elements. For the generalized dead limbs with ten primary attachment points, there is a generalized dead limb with 128 odd elements, a generalized dead limb with 122 odd elements, a generalized dead limb with 131 odd elements, and a generalized dead limb with 125 odd elements. When these values are included, the largest m values increase more linearly. The smallest m values are 2, 3, 4, ..., 10.
The Number of (e, m) Values Equal to Those in Proposition (1)
Let a denote the larger e value and b the smaller for a particular m value that satisfies Proposition (1). For odd integers divisible by 3 less than or equal to 99999999 and generalized dead limbs with two primary attachment points, a plot of the number of (a, m) values (where the m values are along the x-axis) is;
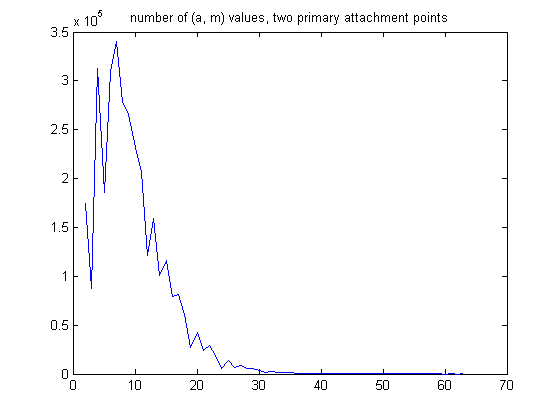
The mean is 9.4538, the standard deviation is 5.3503, and the total sample size is 8314061 . A plot of the number of (a, m) for generalized dead limbs with three primary attachment points is;
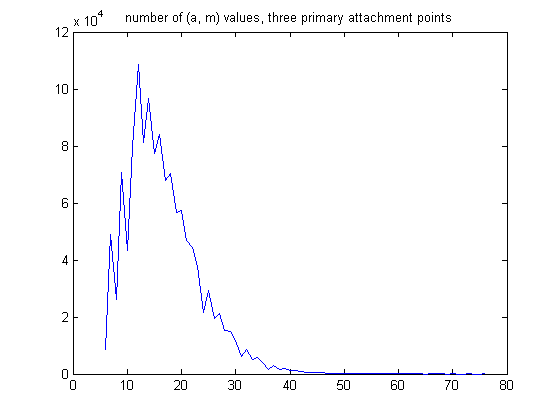
The mean is 16.6291, the standard deviation is 6.5528, and the total samples size is 1285132. A plot of the number of (a, m) values for generalized dead limbs with four primary attachment points is;
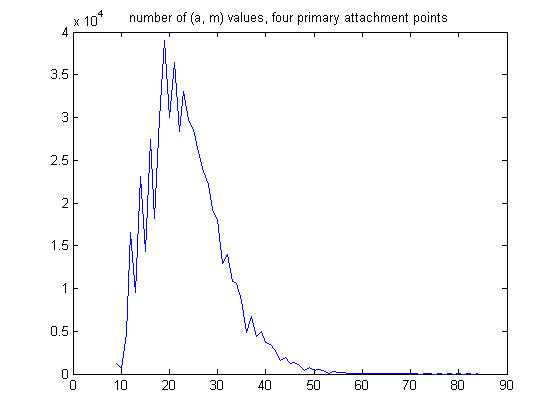
The mean is 23.7463, the standard deviation is 7.5426, and the total sample size is 578362. A plot of the number of (a, m) values for generalized dead limbs with ten primary attachment points is;
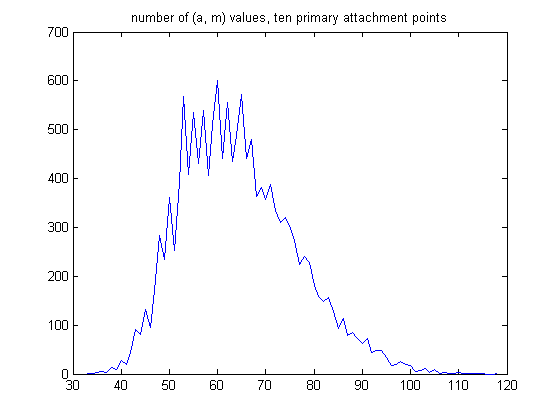
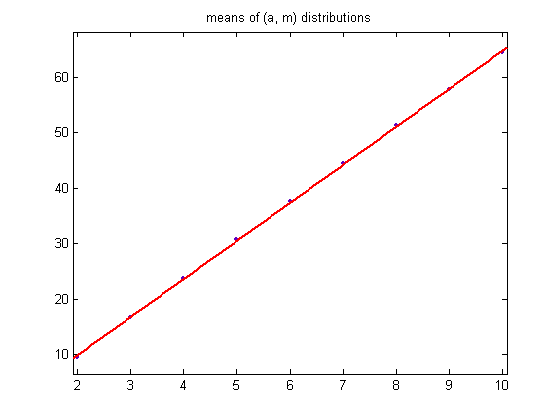
The mean is 64.4667, the standard deviation is 11.8231, and the total sample size is 15032. For a linear least-squares fit of the means, p1=6.876 with a 95% confidence interval of (6.795, 6.958), p2=-3.91 with a 95% confidence interval of (-4.444, -3.376), SSE=0.5016, R-squared=0.9998, and RMSE=0.2677. A plot of the values is;
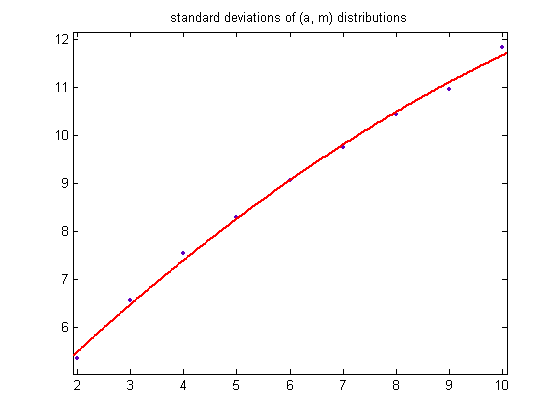
For a quadratic least-squares fit of the standard deviations, p1=-0.0303 with a 95% confidence interval of (-0.04864, -0.01197), p2=1.135 with a 95% confidence interval of (0.9114, 1.359), p3=3.34 with a 95% confidence interval of (2.738, 3.943), SSE=0.1038, R-squared=0.9971, and RMSE=0.1315. A plot of the values is;
For a cubic least-squares fit of the logarithms of the total sample sizes, p1=-0.01409 with a 95% confidence interval of (-0.02557, -0.002612), p2=0.3065 with a 95% confidence interval of (0.09836, 0.5146), p3=-2.711 with a 95% confidence interval of (-3.856, -1.566), p4=20.1 with a 95% confidence interval of (18.25, 21.95), SSE=0.1422, R-squared=0.9956, and RMSE=0.1686). A plot of the values is;
The smallest m values are 2, 6, 9, 12, 16, 19, 24, 30, and 33 and the largest m values are 63, 76, 84, 95, 97, 105, 118, 117, and 118. These values increase roughly quadratically.
For odd integers divisible by 3 less than or equal to 99999999 and generalized dead limbs with two primary attachment points, a plot of the number of (b, m) values is;
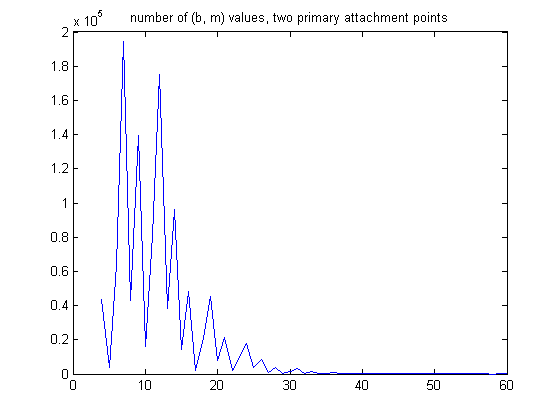
The mean is 11.5641, the standard deviation is 5.2186, and the total sample size is 1109550. A plot of the number of (b, m) values for generalized dead limbs with three primary attachment points is;
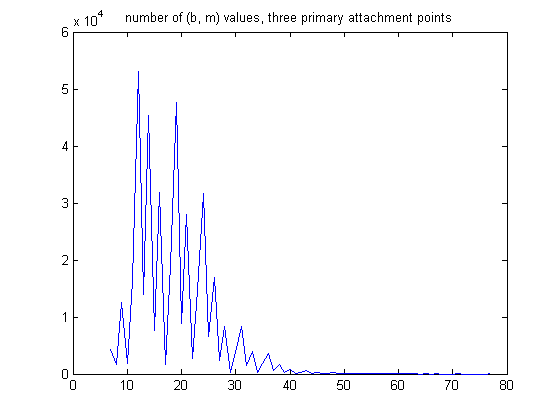
The mean is 18.5215, the standard deviation is 6.6668, and the total sample size is 406447. A plot of the number of (b, m) values for generalized dead limbs with four primary attachment points is;
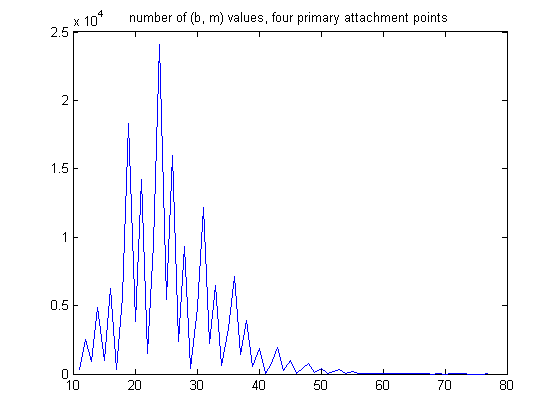
The mean is 25.7644, the standard deviation is 7.5567, and the total sample size is 178008. A plot of the number of (b, m) values for generalized dead limbs having ten primary attachment points is;

The mean is 66.6387, the standard deviation is 12.1296, and the total sample size is 4739. For a linear least-squares fit of the means, p1=6.9 with a 95% confidence interval of (6.767, 7.0321), p2=-1.897 with a 95% confidence interval of (-2.761, -1.034), SSE=1.313, R-squared=0.9995, and RMSE=0.4331. A plot of the values is;

For a quadratic least-squares fit of the standard deviations, p1=-0.03503 with a 95% confidence interval of (-0.07713, 0.007064), p2=1.204 with a 95% confidence interval of (0.6985, 1.718), p3=3.21 with a 95% confidence interval of (1.827, 4.593), SSE=0.5469, R-squared=0.9855, and RMSE=0.3019. A plot of the data is;
For a quadratic least-squares fit of the logarithms of the total sample sizes, p1=0.02815 with a 95% confidence interval of (0.01659, 0.03971), p2=-0.9967 with a 95% confidence interval of (-1.138, -0.8555), p3=15.71 with a 95% confidence interval of (15.33, 16.09), SSE=0.04123, R-squared=0.9984, and RMSE=0.08289. A plot of the data is;
The smallest m values are 4, 7, 11, 14, 18, 23, 28, 31, and 36 and the largest m values are 60, 77, 77, 84, 91, 93, 101, 116, and 120. These values increase roughly quadratically.
Generalized Dead Limbs with Two Primary Attachment Points
The (e, m) values of generalized dead limbs with two primary attachment points can also be modeled with a known probability distribution. In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((5, 4), 2). For c=1, odd integers divisible by 3 less than or equal to 99999999, two primary attachment points, and m =2, the (e, m) value, e>5, is ((6, 7, 8, ..., 27), 2). The respective numbers of (e, m) values are 433470, 216717, 108364, 54189, 27076, 13546, 6785, 3380, 1695, 851, 414, 212, 112, 50, 28, 15, 3, 4, 2, 1, 1, and 1. A histogram of the data is;
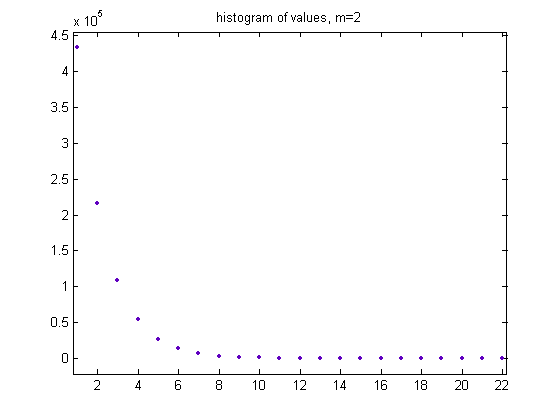
The values decrease exponentially. The mean is 2.0000, the standard deviation is 1.4144 (approximately equal to √2), and the total sample size is 866916. A plot of the logarithms of the histogram values is;

For a linear least-squares fit of the data, the slope is -0.6642 with a 95% confidence interval of (-0.6915, -0.6370), the intercept is 13.45 with a 95% confidence interval of (13.09, 13.81), SSE=3.022, R-squared=0.9923, and RMSE=0.3998.
For c=1, odd integers divisible by 3 less than or equal to 99999999, two primary attachment points, and m =3, the (e, m) value, e>5, is ((6, 7, 8, ..., 28), 3). The respective numbers of (e, m) values are 508002, 425299, 212652, 106329, 53151, 26595, 13295, 6636, 3324, 1658, 834, 420, 205, 112, 51, 19, 11, 10, 3, 2, 1, 0, and 1. A histogram of the data is;
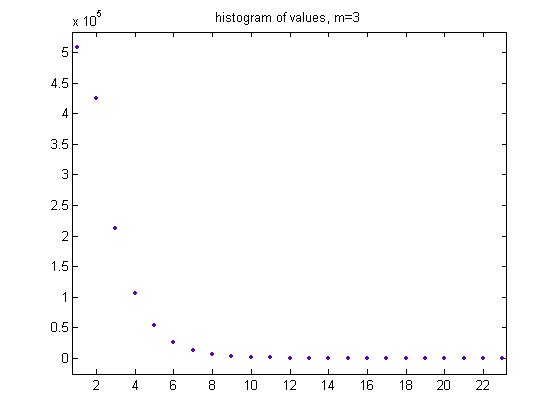
The mean is 2.2522, the standard deviation is 1.4795, and the total sample size is 1358610. When the mean is substantially greater than 2.0, the first bin of the histogram is usually shorter than expected. A plot of the logarithms of the histogram values is;
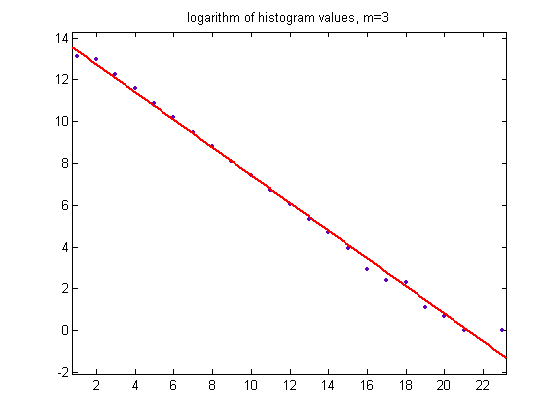
For a linear least-squares fit of the data, the slope is -0.6629 with a 95% confidence interval of (-0.6863, -0.6394), the intercept is 14.06 with a 95% confidence interval of (13.75, 14.37), SSE=2.297, R-squared=0.994, and RMSE=0.3389.
For c=1, odd integers divisible by 3 less than or equal to 99999999, two primary attachment points, and m =4, the (e, m) value, e>6, is ((7, 8, 9, ..., 27), 4). The respective numbers of (e, m) values are 560446, 323083, 161496, 80751, 40394, 20199, 10098, 5069, 2503, 1254, 628, 310, 164, 86, 37, 22, 8, 4, 1, 1, and 1. A histogram of the data is;
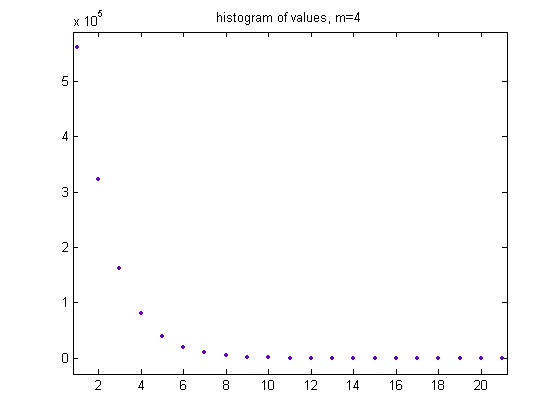
The mean is 2.0709, the standard deviation is 1.4371, and the sample size is 1206555. A plot of the logarithms of the histogram values is;
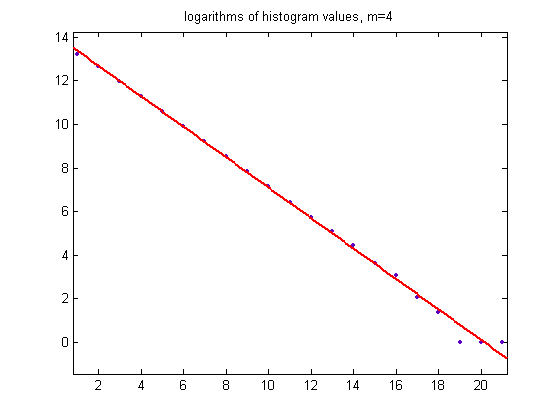
For a linear least-squares fit of the data, the slope is -0.6995 with a 95% confidence interval of (-0.718, -0.6811), the intercept is 14.09 with a 95% confidence interval of (13.86, 14.32), SSE=1.141, R-squared=0.997, and RMSE=0.2451. Some of the variation of the slopes of the linear least-squares fits are due to small deviations in the right-hand tails of the distributions.
A table of the slopes and intercepts (of the linear least-squares fits of the logarithms of the histograms of the values), largest values, means, standard deviations, and sample sizes of the distributions for m up to 20 is;
| 2 | -0.6642 | 13.45 | 22 | 2.0000 | 1.4144 | 866916 |
| 3 | -0.6629 | 14.06 | 23 | 2.2522 | 1.4795 | 1358610 |
| 4 | -0.6995 | 14.09 | 21 | 2.0709 | 1.4371 | 1206555 |
| 5 | -0.6696 | 14.18 | 21 | 2.3428 | 1.5030 | 1333198 |
| 6 | -0.6861 | 13.87 | 21 | 2.1225 | 1.4552 | 1019655 |
| 7 | -0.6735 | 13.37 | 19 | 2.0487 | 1.4325 | 700641 |
| 8 | -0.6885 | 13.60 | 21 | 2.1883 | 1.4749 | 744533 |
| 9 | -0.6992 | 13.20 | 20 | 2.0784 | 1.4408 | 501030 |
| 10 | -0.6797 | 13.23 | 17 | 2.2613 | 1.4950 | 507344 |
| 11 | -0.6908 | 12.80 | 17 | 2.1148 | 1.4552 | 339411 |
| 12 | -0.6715 | 12.18 | 19 | 2.0546 | 1.4402 | 214497 |
| 13 | -0.6461 | 12.13 | 20 | 2.1532 | 1.4733 | 221491 |
| 14 | -0.6846 | 11.83 | 18 | 2.0684 | 1.4403 | 140476 |
| 15 | -0.6946 | 12.00 | 17 | 2.2171 | 1.4899 | 141311 |
| 16 | -0.6700 | 11.34 | 16 | 2.0951 | 1.4464 | 90667 |
| 17 | -0.6597 | 11.35 | 18 | 2.2851 | 1.5102 | 88067 |
| 18 | -0.6323 | 10.64 | 19 | 2.1310 | 1.4624 | 56930 |
| 19 | -0.6180 | 10.15 | 17 | 2.0732 | 1.4594 | 35206 |
| 20 | -0.6271 | 10.25 | 16 | 2.1767 | 1.4824 | 35242 |
For a linear least-squares fit of the logarithms of the sample sizes up to m=62, the slope is -0.2692 with a 95% confidence interval of (-0.275, -0.2633), the intercept is 15.54 with a 95% confidence interval of (15.34, 15.74), SSE=7.207, R-squared=0.9937, and RMSE=0.362. A plot of the data is;
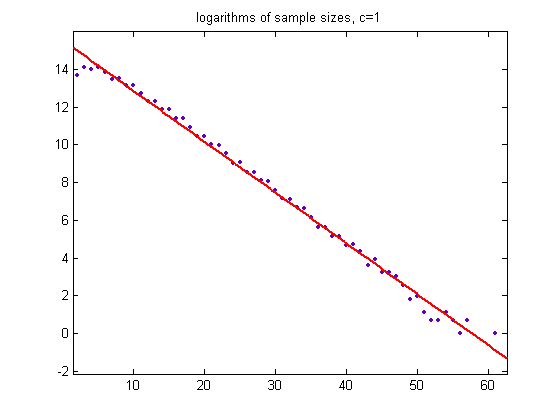
For a linear least-squares fit of the logarithms of the sample sizes for c=461 and m up to 59, the slope is -0.2678 with a 95% confidence interval of (-0.2733, -0.2623), the intercept is 15.5 with a 95% confidence interval of (15.31, 15.64), SSE=6.416, R-squared=0.9943, and RMSE=0.3416. A plot of the data is;
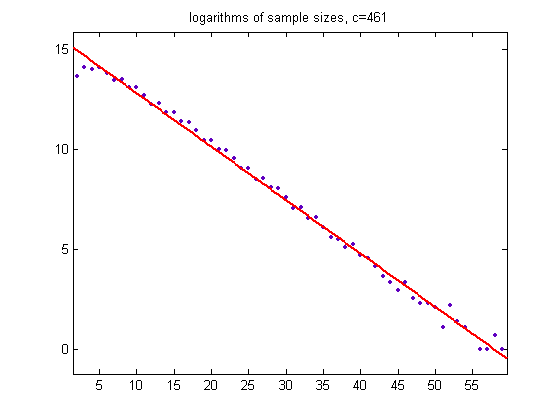
For c=-1, odd integers divisible by 3 less than or equal to 99999999, two primary attachment points, and m =2, the (e, m) value, e>5, is ((6, 7, 8, ..., 25), 2). The respective numbers of (e, m) values are 433433, 216735, 108362, 54174, 27106, 13545, 6759, 3393, 1692, 842, 432, 212, 98, 56, 26, 12, 10, 3, 0, and 1. A table of the corresponding slopes and intercepts (of the linear least-squares fits of the logarithms of the histograms of the values), means, standard deviations, largest values, and sample sizes of the distributions for different c values is;
| c=1 | -0.6642 | 13.45 | 2.0000 | 1.4144 | 22 | 866916 |
| -1 | -0.6875 | 13.64 | 2.0000 | 1.4140 | 20 | 866891 |
| 5 | -0.6734 | 13.31 | 2.0000 | 1.4143 | 21 | 693533 |
| 7 | -0.6927 | 13.52 | 2.0000 | 1.4141 | 19 | 743051 |
| 11 | -0.6827 | 13.50 | 2.0000 | 1.4143 | 21 | 788089 |
| 13 | -0.6425 | 13.19 | 2.0000 | 1.4145 | 24 | 800221 |
| 17 | -0.6870 | 13.57 | 2.0000 | 1.4140 | 19 | 815905 |
| -17 | -0.6815 | 13.53 | 2.0000 | 1.4142 | 20 | 815910 |
| 19 | -0.6923 | 13.61 | 2.0000 | 1.4141 | 20 | 821287 |
| -19 | -0.6150 | 13.01 | 2.0001 | 1.4147 | 25 | 821269 |
| 23 | -0.6842 | 13.56 | 1.9999 | 1.4140 | 20 | 829214 |
| -23 | -0.6640 | 13.41 | 2.0000 | 1.4142 | 22 | 829204 |
| 25 | -0.6823 | 13.38 | 2.0000 | 1.4142 | 19 | 693526 |
| -25 | -0.6773 | 13.33 | 2.0000 | 1.4140 | 21 | 693517 |
| 29 | -0.6588 | 13.36 | 2.0000 | 1.4142 | 23 | 837010 |
| -29 | -0.6645 | 13.42 | 2.0000 | 1.4143 | 22 | 837011 |
| 31 | -0.6834 | 13.56 | 2.0000 | 1.4141 | 21 | 838947 |
| -31 | -0.6812 | 13.55 | 2.0000 | 1.4143 | 21 | 838936 |
| 35 | -0.6927 | 13.29 | 1.9999 | 1.4140 | 19 | 594457 |
| 37 | -0.6724 | 13.48 | 2.0000 | 1.4142 | 22 | 843464 |
| 41 | -0.6822 | 13.56 | 2.0000 | 1.4142 | 21 | 845747 |
| 43 | -0.6658 | 13.44 | 2.0000 | 1.4142 | 22 | 846743 |
| 47 | -0.6884 | 13.60 | 2.0000 | 1.4141 | 21 | 848461 |
| 49 | -0.6593 | 13.27 | 2.0000 | 1.4143 | 22 | 743065 |
| -119 | -0.6792 | 13.36 | 2.0000 | 1.4142 | 20 | 699350 |
| 175 | -0.6763 | 13.18 | 1.9999 | 1.4138 | 19 | 594457 |
| 221 | -0.6828 | 13.45 | 2.0000 | 1.4142 | 21 | 753159 |
| 461 | -0.6599 | 13.41 | 2.0000 | 1.4143 | 23 | 865046 |
Other than c=1, there are cycles with attachment points for these c values. All such c values with an absolute value less than or equal to 49 are included. A few c values with relatively large absolute values are also included. The sample sizes for positive and negative c values such as 17 and -17 are approximately equal. The respective lower bounds of the odd integers divisible by 3 that were used (for c=1, -1, 5, 7, ..., 461) are 3, 3, -3, -3, -21, -3, -9, 3, -3, -33, 3, -111, 3, -33, 3, -27, 3, -99, -9, -87, -45, -81, -69, -201, 3, -291, and -819. These values are used to include the t values of all the known cycles (although this is not necessary in the above). This will have a small effect on the sample sizes.
A table of the corresponding means, standard deviations, largest values, sample sizes, and slopes and intercepts (of the linear least-squares fits of the logarithms of the histograms of the values) for different m values (the first column) and for c=-1 is;
| 2 | 2.0000 | 1.4140 | 20 | 866891 | -0.6875 | 13.64 |
| 3 | 2.2521 | 1.4791 | 21 | 1358604 | -0.6891 | 14.26 |
| 4 | 2.0711 | 1.4377 | 23 | 1206558 | -0.6626 | 13.83 |
| 5 | 2.3424 | 1.5016 | 21 | 1333128 | -0.6863 | 14.27 |
| 6 | 2.1224 | 1.4547 | 19 | 1019656 | -0.7092 | 14.03 |
| 7 | 2.0482 | 1.4314 | 20 | 700617 | -0.6691 | 13.32 |
| 8 | 2.1887 | 1.4754 | 20 | 744524 | -0.6795 | 13.57 |
| 9 | 2.0798 | 1.4449 | 18 | 501041 | -0.6619 | 13.00 |
| 10 | 2.2617 | 1.4953 | 18 | 507408 | -0.6770 | 13.22 |
A table of the corresponding means, standard deviations, largest values, sample sizes, and slopes and intercepts (of the linear least-squares fits of the logarithms of the histograms of the values) for different m values and c=5 is;
| 2 | 2.0000 | 1.4143 | 21 | 693533 | -0.6734 | 13.31 |
| 3 | 2.2522 | 1.4794 | 25 | 1086878 | -0.6382 | 13.62 |
| 4 | 2.0708 | 1.4366 | 22 | 965256 | -0.6836 | 13.74 |
| 5 | 2.3425 | 1.5021 | 20 | 1066488 | -0.6862 | 14.06 |
| 6 | 2.1224 | 1.4545 | 21 | 815698 | -0.6867 | 13.64 |
| 7 | 2.0487 | 1.4331 | 21 | 560508 | -0.6644 | 13.08 |
| 8 | 2.1883 | 1.4742 | 20 | 595586 | -0.6963 | 13.44 |
| 9 | 2.0789 | 1.4437 | 22 | 400882 | -0.6619 | 12.71 |
| 10 | 2.2615 | 1.4964 | 21 | 406043 | -0.6520 | 12.82 |
A table of the corresponding means, standard deviations, largest values, sample sizes, and slopes and intercepts (of the linear least-squares fits of the logarithms of the histograms of the values) for different m values and c=7 is;
| 2 | 2.0000 | 1.4141 | 19 | 743051 | -0.6927 | 13.52 |
| 3 | 2.2521 | 1.4794 | 23 | 1164526 | -0.6513 | 13.82 |
| 4 | 2.0711 | 1.4377 | 25 | 1034200 | -0.6192 | 13.34 |
| 5 | 2.3426 | 1.5021 | 21 | 1142712 | -0.6786 | 14.07 |
| 6 | 2.1224 | 1.4555 | 21 | 873982 | -0.6740 | 13.63 |
| 7 | 2.0484 | 1.4324 | 22 | 600497 | -0.6642 | 13.11 |
| 8 | 2.1885 | 1.4753 | 23 | 638177 | -0.6539 | 13.19 |
| 9 | 2.0795 | 1.4436 | 19 | 429391 | -0.6884 | 12.99 |
| 10 | 2.2627 | 1.4984 | 19 | 434925 | -0.6704 | 13.01 |
A plot of the above means is;
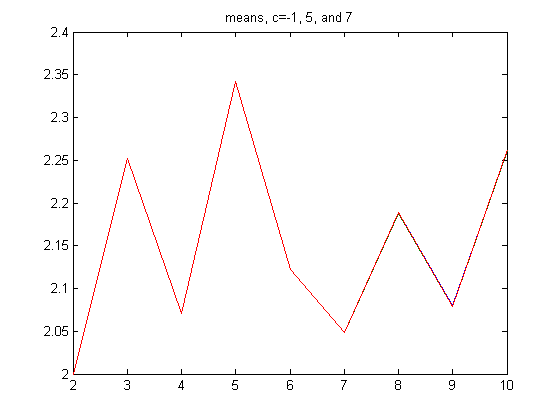
A plot of the above standard deviations is;
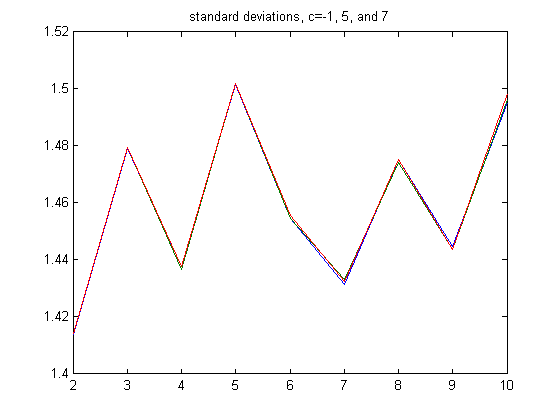
A plot of the above sample sizes is;
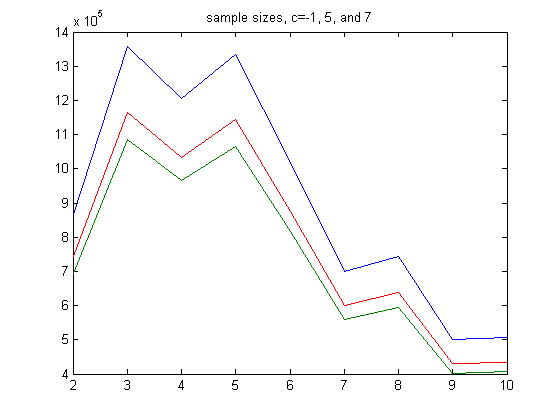
The sample sizes for c=-1 are about 1+1/(5-1) times larger than those for c=5 and about 1+1/(7-1) times larger than those for c=7.
A plot of the corresponding means for c=11, 13, and 17 is;

A plot of the corresponding standard deviations for c=11, 13, and 17 is;

A plot of the corresponding sample sizes for c=11, 13, and 17 is;

The sample sizes for c=-1 are about 1+1/(11-1) times as large as the sample sizes for c=11, about 1+1/(13-1) times as large as the sample sizes for c=13, and about 1+1/(17-1) times as large as the sample sizes for c=17.
The distribution of (e, m) values appears to be about the same for all c values.
Generalized Dead Limbs with Three Primary Attachment Points
In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((5, 4), 3). For c=1, odd integers divisible by 3 less than or equal to 99999999, three primary attachment points, and m =3, the (e, m) value, e>5, is ((6, 7, 8, ..., 29), 3). The respective numbers of (e, m) values are 0, 21845, 65119, 59621, 43349, 28489, 17614, 10496, 6110, 3454, 1941, 1093, 586, 318, 181, 96, 50, 26, 14, 8, 4, 3, 3, and 1. For a Weibull probability fit of the data, the scaling factor is 5.2725 with a 95% confidence interval of (5.2635, 5.2815) and the shaping factor is 2.3801 with a 95% confidence interval of (2.3736, 2.3866). A histogram of the data along with the Weibull probability distribution is;
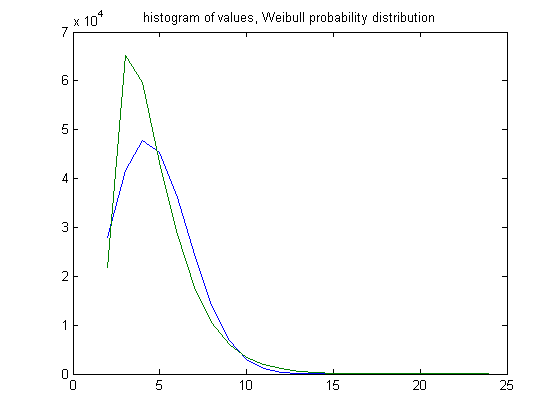
For m<10, a Weibull probability distribution does not model the distribution very well . In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((9, 8), 10). For c=1, odd integers divisible by 3 less than or equal to 99999999, three primary attachment points, and m =10, the (e, m) value, e>9, is ((10, 11, 12,..., 33), 10). The respective numbers of (e, m) values are 120191, 198727, 212350, 172952, 120433, 77306, 47340, 27966, 16124, 9202, 5020, 2766, 1599, 775, 508, 235, 127, 71, 23, 14, 8, 7, 5, and 1. For a Weibull probability fit of the data, the scaling factor is 4.2829 with a 95% confidence interval of (4.2782, 4.2877) and the shaping factor is 1.8408 with a 95% confidence interval of (1.8381, 1.8435). A histogram of the data along with the Weibull probability distribution is;
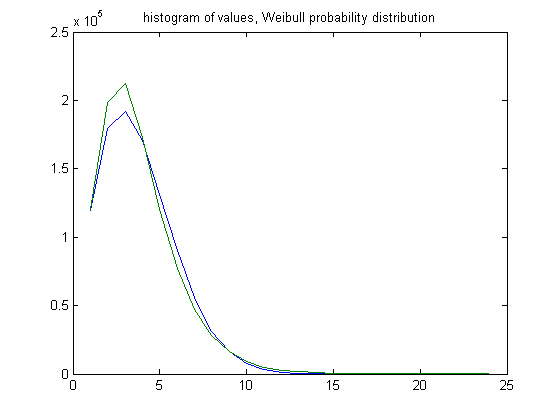
For larger m values, the Weibull probability distribution usually models the distribution fairly well except for the first or second histogram values. In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((13, 12), 16). For c=1, odd integers divisible by 3 less than or equal to 99999999, three primary attachment points, and m =16, the (e, m) value, e>13, is ((14, 15, 16,..., 37), 16). The respective numbers of (e, m) values are 98887, 95913, 76853, 54085, 34771, 21402, 12651, 7337, 4183, 2428, 1285, 714, 420, 199, 109, 63, 23, 16, 7, 6, 3, 1, 1, and 1. For a Weibull probability fit of the data, the scaling parameter is 3.5088 with a 95% confidence interval of (3.5018, 3.5159) and the shaping parameter is 1.6197 with a 95% confidence interval of (1.6160, 1.6234). A histogram of the values along with the Weibull probability distribution is;
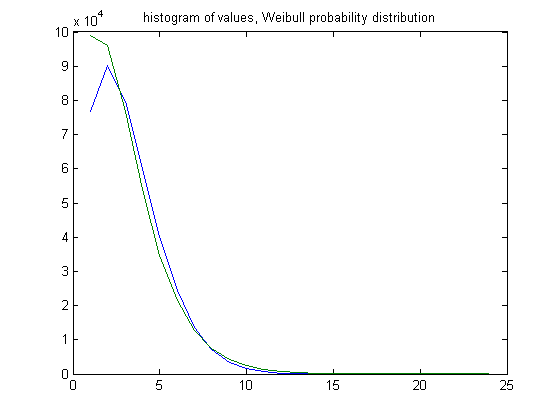
For m≥19, the Weibull probability distribution usually models the distribution fairly well except for the first histogram value. In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((15, 14), 19). For c=1, odd integers divisible by 3 less than or equal to 99999999, three primary attachment points, and m =19, the (e, m) value, e>19, is ((30, 21, 22,..., 37), 19). The respective numbers of (e, m) values are 60213, 51208, 38365, 25594, 16246, 9861, 5680, 3302, 1826, 1051, 585, 289, 184, 76, 58, 27, 13, 7, 6, and 2. For a Weibull probability fit of the data, the scaling parameter is 3.2898 with a 95% confidence interval of (3.2804, 3.2991) and the shaping parameter is 1.5798 with a 95% confidence interval of (1.5749, 1.5848). A histogram of the data with the Weibull probability distribution is;

A plot of the logarithms of the histogram values is;
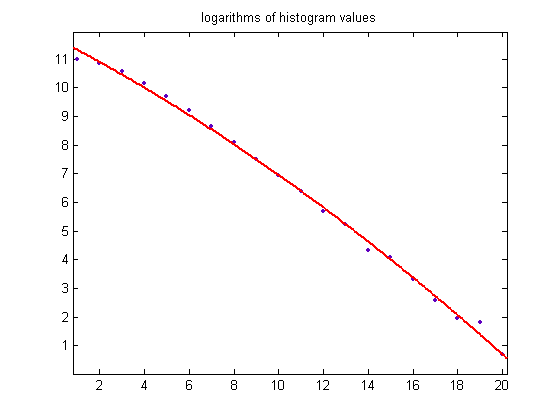
For a quadratic least-squares fit of the data, p1=-0.007412 with a 95% confidence interval of (-0.01022, -0.004604), p2=-0.4045 with a 95% confidence interval of (-0.4652, -0.3437), p3=11.74 with a 95% confidence interval of (11.46, 12.02), SSE=0.5286, R-squared=0.9975, and RMSE=0.1763. For other such m values, the logarithms of the histogram values decrease approximately quadratically.
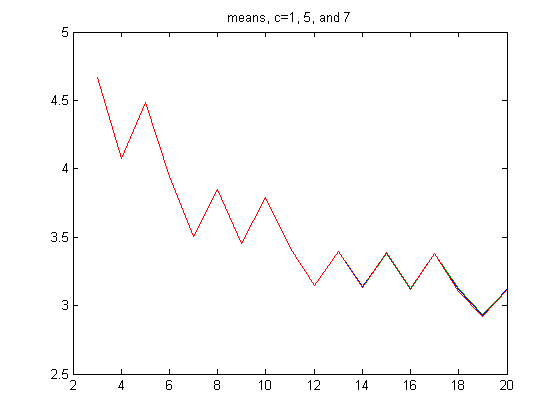
A table of the means, standard deviations, largest values, and sample sizes of the distributions for m=3, 4, 5, ..., 20 and c=1 is;
| 3 | 4.6647 | 2.0559 | 24 | 260421 |
| 4 | 4.0748 | 2.0942 | 25 | 556822 |
| 5 | 4.4871 | 2.1329 | 24 | 808226 |
| 6 | 3.9437 | 2.1496 | 24 | 978167 |
| 7 | 3.5040 | 2.1148 | 22 | 1034949 |
| 8 | 3.8511 | 2.1737 | 24 | 1097063 |
| 9 | 3.4565 | 2.1248 | 23 | 1027133 |
| 10 | 3.7887 | 2.1890 | 24 | 1013750 |
| 11 | 3.4199 | 2.1334 | 23 | 887124 |
| 12 | 3.1468 | 2.0662 | 24 | 732567 |
| 13 | 3.3939 | 2.1442 | 22 | 704470 |
| 14 | 3.1389 | 2.0774 | 22 | 562302 |
| 15 | 3.3804 | 2.1389 | 25 | 526772 |
| 16 | 3.1207 | 2.0761 | 24 | 411358 |
| 17 | 3.3785 | 2.1421 | 24 | 378738 |
| 18 | 3.1199 | 2.0843 | 22 | 291645 |
| 19 | 2.9301 | 2.0119 | 20 | 214593 |
| 20 | 3.1267 | 2.0797 | 20 | 200353 |
A table of the means, standard deviations, largest values, and sample sizes of the distributions for m=3, 4, 5, ..., 20 and c=5 is;
| 3 | 4.6646 | 2.0553 | 25 | 208333 |
| 4 | 4.0742 | 2.0925 | 25 | 445429 |
| 5 | 4.4863 | 2.1305 | 26 | 646522 |
| 6 | 3.9429 | 2.1477 | 26 | 782442 |
| 7 | 3.5026 | 2.1104 | 26 | 827773 |
| 8 | 3.8500 | 2.1721 | 27 | 877720 |
| 9 | 3.4564 | 2.1242 | 24 | 821579 |
| 10 | 3.7915 | 2.1928 | 22 | 811520 |
| 11 | 3.4172 | 2.1307 | 26 | 709220 |
| 12 | 3.1473 | 2.0671 | 21 | 585422 |
| 13 | 3.3961 | 2.1434 | 22 | 563808 |
| 14 | 3.1324 | 2.0709 | 23 | 449128 |
| 15 | 3.3788 | 2.1377 | 24 | 421244 |
| 16 | 3.1199 | 2.0795 | 22 | 329778 |
| 17 | 3.3805 | 2.1486 | 21 | 302778 |
| 18 | 3.1249 | 2.0915 | 22 | 233387 |
| 19 | 2.9334 | 2.0242 | 20 | 172152 |
| 20 | 3.1144 | 2.0816 | 23 | 160662 |
A table of the means, standard deviations, largest values, and sample sizes of the distributions for m=3, 4, 5, ..., 20 and c=7 is;
| 3 | 4.6642 | 2.0539 | 23 | 223208 |
| 4 | 4.0745 | 2.0933 | 23 | 477256 |
| 5 | 4.4874 | 2.1338 | 24 | 692790 |
| 6 | 3.9425 | 2.1462 | 25 | 838339 |
| 7 | 3.5034 | 2.1137 | 24 | 887074 |
| 8 | 3.8514 | 2.1749 | 24 | 940204 |
| 9 | 3.4575 | 2.1282 | 26 | 880274 |
| 10 | 3.7896 | 2.1902 | 26 | 869183 |
| 11 | 3.4209 | 2.1352 | 23 | 760544 |
| 12 | 3.1505 | 2.0709 | 24 | 627840 |
| 13 | 3.3984 | 2.1495 | 23 | 603564 |
| 14 | 3.1321 | 2.0786 | 25 | 481083 |
| 15 | 3.3902 | 2.1520 | 24 | 452213 |
| 16 | 3.1219 | 2.0829 | 22 | 352514 |
| 17 | 3.3804 | 2.1461 | 24 | 325325 |
| 18 | 3.1067 | 2.0713 | 25 | 249044 |
| 19 | 2.9198 | 2.0020 | 21 | 183799 |
| 20 | 3.1180 | 2.0696 | 21 | 171912 |
A plot of the means is;
A plot of the standard deviations is;

A plot of the sample sizes is;
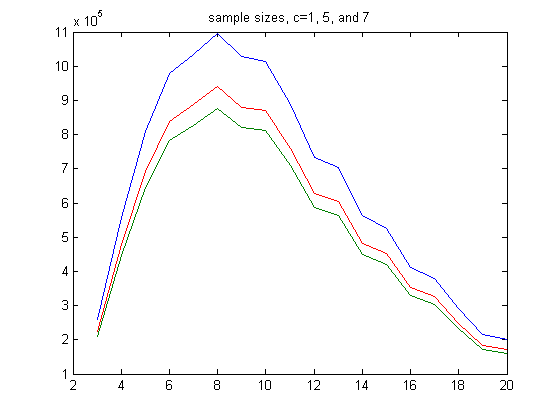
The sample sizes for c=1 are about 1+1/(5-1) times larger than those for c=5 and about 1+1/(7-1) times larger than those for c=7.
Generalized Dead Limbs with Four Primary Attachment Points
In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((9, 8), 10). For c=1, odd integers divisible by 3 less than or equal to 99999999, four primary attachment points, and m =10, the (e, m) value, e>9, is ((10, 11, 12,..., 34), 10). The respective numbers of (e, m) values are 8552, 37929, 87873, 129726, 142651, 128540, 102369, 75038, 51571, 34251, 21518, 13527, 8135, 4865, 2956, 1665, 981, 530, 303, 184, 123, 69, 63, 11, and 3. For a Weibull probability fit of the data, the scaling parameter is 6.8303 with a 95% confidence interval of (6.8239, 6.8368) and the shaping parameter is 2.3749 with a 95% confidence interval of (2.3712, 2.3787). A histogram of the data with the Weibull probability distribution is;

For 9≥m≥4, the Weibull probability distribution models the distributions about as well or worse. In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((12, 11), 15). For c=1, odd integers divisible by 3 less than or equal to 99999999, four primary attachment points, and m =15, the (e, m) value, e>12, is ((13, 14, 15,..., 37), 15). The respective numbers of (e, m) values are 42121, 82822, 117517, 131474, 122852, 101651, 76517, 54010, 36407, 23785, 14813, 9221, 5490, 3370, 2026, 1109, 574, 277, 159, 98, 48, 28, 17, 16, and 1. For a Weibull probability fit, the scaling parameter is 5.8926 with a 95% confidence interval of (5.8859, 5.8993) and the shaping parameter is 2.0066 with a 95% confidence interval of (2.0033, 2.0099). A histogram of the data with the Weibull probability distribution is;

For 14≥m≥11, the Weibull probability distribution models the distributions about as well as for m=15. In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((15, 14), 20). For c=1, odd integers divisible by 3 less than or equal to 99999999, four primary attachment points, and m =20, the (e, m) value, e>15, is ((16, 17, 18,..., 39), 15). The respective numbers of (e, m) values are 48241, 68183, 77112, 74422, 63515, 49181, 35957, 24549, 16096, 10320, 6423, 3885, 2382, 1385, 791, 461, 238, 142, 67, 32, 25, 9, 6, and 2. For a Weibull probability fit of the data, the scaling parameter is 5.1772 with a 95% confidence interval of (5.1686, 5.1858) and the shaping parameter is 1.7919 with a 95% confidence interval of (1.7881, 1.7958). A histogram of the data with the Weibull probability distribution is;
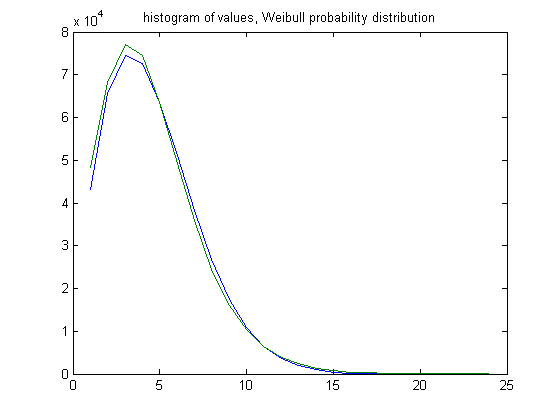
For 19≥m≥16, the Weibull probability distribution models the distributions almost as well as for m=20. In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((18, 17), 25). For c=1, odd integers divisible by 3 less than or equal to 99999999, four primary attachment points, and m =25, the (e, m) value, e>18, is ((19, 20, 21,..., 44), 25). The respective numbers of (e, m) values are 32147, 36796, 36386, 31779, 25430, 18871, 13256, 9023, 5731, 3631, 2210, 1328, 779, 507, 287, 193, 95, 49, 31, 11, 5, 3, 1, 0, 0, and 1. For a Weibull probability fit of the data, the scaling parameter is 4.6478 with a 95% confidence interval of (4.6354, 4.6602) and the shaping parameter is 1.6614 with a 95% confidence interval of (`.6561, 1.6667). A histogram of the data with the Weibull probability distribution is;

The Weibull probability distribution models the distribution fairly well except for the first two histogram values. In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((21, 20), 30). For c=1, odd integers divisible by 3 less than or equal to 99999999, four primary attachment points, and m =30, the (e, m) value, e>21, is ((22, 23, 24,..., 44), 30). The respective numbers of (e, m) values are 15428, 15761, 14044, 11763, 8877, 6209, 4318, 2701, 1803, 1125, 629, 437, 271, 133, 105, 61, 25, 18, 12, 3, 2, and 1. For a Weibull probability fit of the data, the scaling parameter is 4.2624 with a 95% confidence interval of (4.2433, 4.2816) and the shaping parameter is 1.5922 with a 95% confidence interval of (1.5841, 1.6004). A histogram of the data with the Weibull probability distribution is;
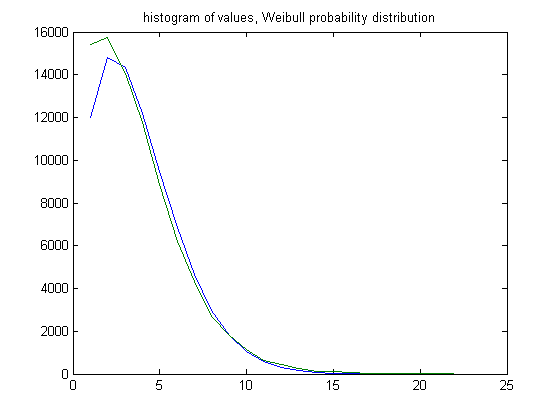
A plot of the logarithms of the histogram values is;
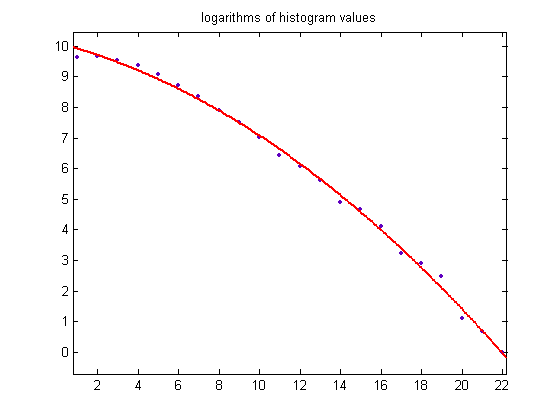
For a quadratic least-squares fit of the data, p1=-0.01324 with a 95% confidence interval of (-0.01543, -0.01106), p2=-0.1697 with a 95% confidence interval of (-0.2215, -0.118), p3=10.1 with a 95% confidence interval of (9.842, 10.36), SSE=0.5866, R-squared=0.9971, and RMSE=0.1757.
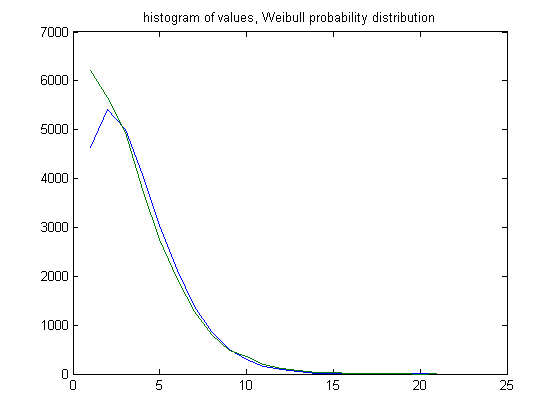
In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((24, 23), 35). For c=1, odd integers divisible by 3 less than or equal to 99999999, four primary attachment points, and m =35, the (e, m) value, e>24, is ((25, 26, 27,..., 44), 35). The respective numbers of (e, m) values are 6220, 5652, 4950, 3773, 2745, 1927, 1283, 803, 488, 358, 193, 113, 65, 39, 29, and 20. For a Weibull probability fit of the data, the scaling parameter is 3.9859 with a 95% confidence interval of (3.9545, 4.0176) and the shaping parameter is 1.5481 with a 95% confidence interval of (1.5347, 1.5616). A histogram of the data with the Weibull probability distribution is;
A plot of the logarithms of the histogram values is;
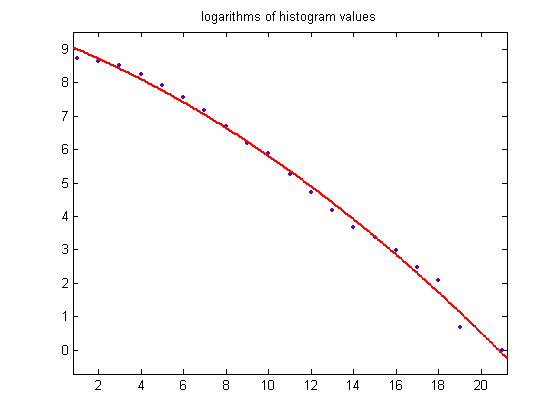
For a quadratic least-squares fit of the data, p1=-0.009192 with a 95% confidence interval of (-0.01224, -0.00614), p2=-0.2536 with a 95% confidence interval of (-0.3209, -0.1862), p3=9.261 with a 95% confidence interval of (8.946, 9.577), SSE=0.7158, R-squared=0.9949, and RMSE=0.2052.
A plot of the logarithm of the Weibull probability distribution is;
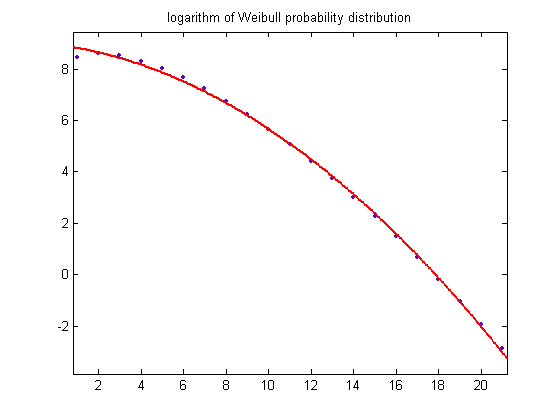
For a quadratic least-squares fit of the data, p1=-0.02217 with a 95% confidence interval of (-0.02409, -0.02026), p2=-0.1048 with a 95% confidence interval of (-0.1482, -0.0614), p3=8.937 with a 95% confidence interval of (8.73, 9.144), SSE=0.3355, R-squared=0.9988, and RMSE=0.1365.
A table of the means, standard deviations, largest values, and samples sizes of the distributions for m=4, 5, 6, ..., 15 and c=-1 is;
| 4 | 6.6602 | 2.4837 | 22 | 65080 |
| 5 | 7.0542 | 2.5279 | 23 | 188040 |
| 6 | 6.4441 | 2.5594 | 24 | 343072 |
| 7 | 5.8398 | 2.5908 | 22 | 503860 |
| 8 | 6.2338 | 2.6215 | 25 | 649600 |
| 9 | 5.6417 | 2.6410 | 23 | 767079 |
| 10 | 6.0431 | 2.6802 | 24 | 853168 |
| 11 | 5.4739 | 2.6869 | 24 | 900013 |
| 12 | 4.9634 | 2.6714 | 24 | 905784 |
| 13 | 5.3314 | 2.7249 | 25 | 907670 |
| 14 | 4.8480 | 2.6893 | 24 | 859381 |
| 15 | 5.2098 | 2.7466 | 24 | 825924 |
A table of the means, standard deviations, largest values, and samples sizes of the distributions for m=4, 5, 6, ..., 15 and c=5 is;
| 4 | 6.6678 | 2.5057 | 26 | 52091 |
| 5 | 7.0533 | 2.5278 | 27 | 150385 |
| 6 | 6.4448 | 2.5621 | 26 | 274342 |
| 7 | 5.8401 | 2.5938 | 27 | 403129 |
| 8 | 6.2337 | 2.6217 | 27 | 519746 |
| 9 | 5.6418 | 2.6450 | 28 | 613552 |
| 10 | 6.0386 | 2.6785 | 26 | 681481 |
| 11 | 5.4768 | 2.6890 | 27 | 720699 |
| 12 | 5.9544 | 2.6654 | 27 | 724496 |
| 13 | 5.3257 | 2.7154 | 27 | 724574 |
| 14 | 4.8466 | 2.6856 | 27 | 686861 |
| 15 | 5.2031 | 2.7380 | 28 | 662128 |
A table of the means, standard deviations, largest values, and samples sizes of the distributions for m=4, 5, 6, ..., 15 and c=-119 is;
| 4 | 6.6651 | 2.4968 | 24 | 52520 |
| 5 | 7.0539 | 2.5306 | 25 | 151693 |
| 6 | 6.4462 | 2.5633 | 24 | 276846 |
| 7 | 5.8425 | 2.6003 | 25 | 406569 |
| 8 | 6.2391 | 2.6321 | 26 | 524331 |
| 9 | 5.6497 | 2.6586 | 28 | 619485 |
| 10 | 6.0492 | 2.6942 | 29 | 688640 |
| 11 | 5.4844 | 2.7053 | 27 | 726745 |
| 12 | 4.9646 | 2.6792 | 26 | 730874 |
| 13 | 5.3401 | 2.7362 | 28 | 731951 |
| 14 | 4.8504 | 2.6904 | 31 | 693669 |
| 15 | 5.2084 | 2.7501 | 29 | 665941 |
A table of the means, standard deviations, largest values, and samples sizes of the distributions for m=4, 5, 6, ..., 15 and c=175 is;
| 4 | 6.6666 | 2.4967 | 23 | 44647 |
| 5 | 7.0543 | 2.5321 | 25 | 128913 |
| 6 | 6.4451 | 2.5600 | 25 | 235321 |
| 7 | 5.8409 | 2.5956 | 24 | 345505 |
| 8 | 6.2368 | 2.6309 | 26 | 445671 |
| 9 | 5.6488 | 2.6574 | 25 | 526223 |
| 10 | 6.0449 | 2.6869 | 27 | 584915 |
| 11 | 5.4819 | 2.7042 | 27 | 617593 |
| 12 | 4.9608 | 2.6724 | 26 | 620894 |
| 13 | 5.3306 | 2.7258 | 28 | 621612 |
| 14 | 4.8495 | 2.6928 | 26 | 589791 |
| 15 | 5.2031 | 2.7436 | 28 | 566770 |
A table of the means, standard deviations, largest values, and samples sizes of the distributions for m=4, 5, 6, ..., 15 and c=221 is;
| 4 | 6.6648 | 2.4946 | 27 | 56567 |
| 5 | 7.0543 | 2.5316 | 28 | 163312 |
| 6 | 6.4436 | 2.5620 | 29 | 297948 |
| 7 | 5.8409 | 2.5979 | 28 | 437769 |
| 8 | 6.2372 | 2.6275 | 29 | 564545 |
| 9 | 5.6465 | 2.6529 | 27 | 666689 |
| 10 | 6.0465 | 2.6848 | 28 | 741919 |
| 11 | 5.4756 | 2.6935 | 27 | 782160 |
| 12 | 4.9653 | 2.6778 | 29 | 786962 |
| 13 | 5.3336 | 2.7281 | 28 | 788083 |
| 14 | 4.8468 | 2.6880 | 28 | 746827 |
| 15 | 5.2011 | 2.7402 | 27 | 717105 |
A table of the means, standard deviations, largest values, and samples sizes of the distributions for m=4, 5, 6, ..., 15 and c=461 is;
| 4 | 6.6680 | 2.5064 | 28 | 64982 |
| 5 | 7.0565 | 2.5372 | 31 | 187648 |
| 6 | 6.4509 | 2.5771 | 34 | 342457 |
| 7 | 5.8437 | 2.6033 | 29 | 502929 |
| 8 | 6.2411 | 2.6401 | 30 | 648581 |
| 9 | 5.6508 | 2.6616 | 30 | 766073 |
| 10 | 6.0479 | 2.6931 | 30 | 851732 |
| 11 | 5.4813 | 2.6997 | 29 | 898887 |
| 12 | 4.9671 | 2.6822 | 30 | 904473 |
| 13 | 5.3363 | 2.7316 | 32 | 906132 |
| 14 | 4.8497 | 2.6952 | 29 | 857815 |
| 15 | 5.2106 | 2.7478 | 25 | 824315 |
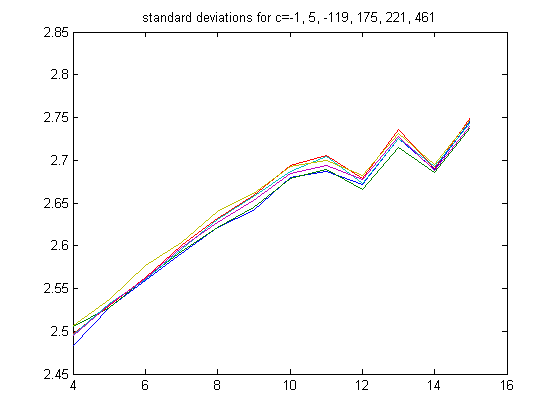
A plot of the means for c=-1, 5, -119, 175, 221, and 461 is;

A plot of the standard deviations for c=-1, 5, -119, 175, 221, and 461 is;
A plot of the sample sizes for c=-1, 5, -119, 175, 221, and 461 is;
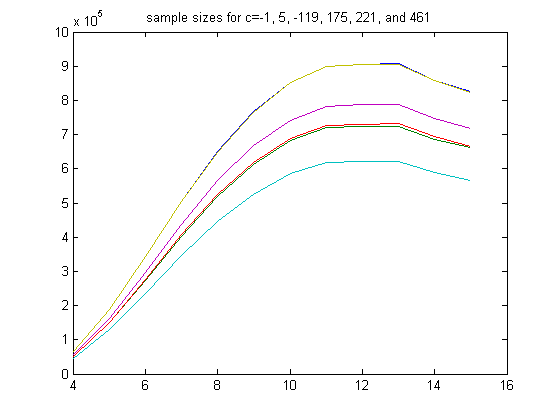
The sample sizes for c=-1 and 461 are almost equal and the sample sizes for c=5 and -119 are roughly equal. The sample size for c=-1 is almost 1+1/(5-1) times as large as the sample size for c=5 and almost 1+1/(461-1) times are large as the sample size for c=461 (5 and 461 are primes whereas 119, 175, and 221 are not).
Generalized Dead Limbs with Six Primary Attachment Points
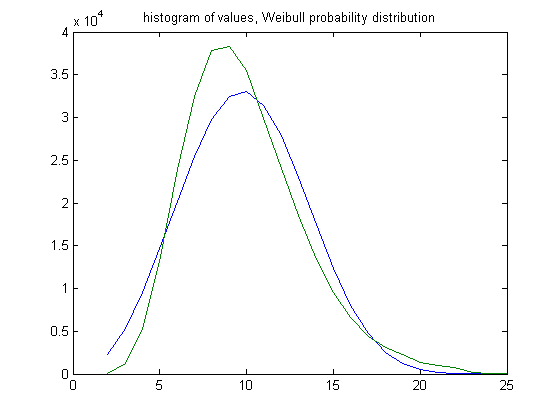
In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((11, 10), 12). For c=1, odd integers divisible by 3 less than or equal to 99999999, six primary attachment points, and m =12, the (e, m) value, e>11, is ((12, 13, 14,..., 36), 12). The respective numbers of (e, m) values are (0, 112, 1181, 5276, 13202, 23928, 32495, 37846, 38271, 35460, 29860, 24091, 18495, 13336, 9560, 6652, 4347, 3066, 2287, 1290, 976, 764, 186, 33, and 2. For a Weibull probability fit of the data, the scaling parameter is 11.0701 with a 95% confidence interval of (11.0566, 11.0835) and the shaping parameter is 3.1041 with a 95% confidence interval of (3.0960, 3.1122). A histogram of the data with the Weibull probability distribution is;
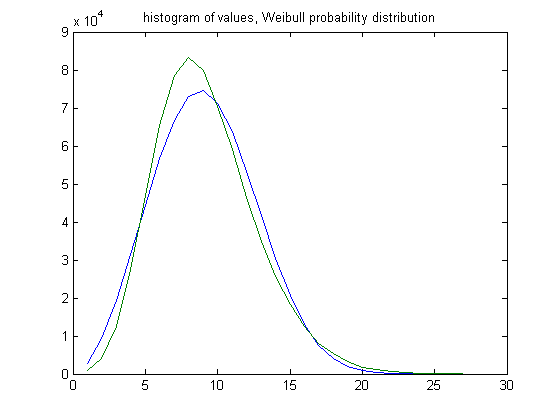
In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((14, 13), 18). For c=1, odd integers divisible by 3 less than or equal to 99999999, six primary attachment points, and m =18, the (e, m) value, e>14, is ((15, 16, 17,..., 41), 18). The respective numbers of (e, m) values are 939, 4203, 12491, 27575, 46958, 65460, 78554, 83417, 79907, 70393, 59105, 46537, 34868, 25694, 18264, 12594, 8039, 5304, 3204, 1812, 1191, 542, 286, 219, 65, 23, and 3. For a Weibull probability fit, the scaling parameter is 10.2901 with a 95% confidence interval of (10.2810, 10.2991) and the shaping parameter is 2.8271 with a 95% confidence interval of (2.8221, 2.8322). A histogram of the data with the Weibull probability distribution is;
In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((18, 17), 24). For c=1, odd integers divisible by 3 less than or equal to 99999999, six primary attachment points, and m =24, the (e, m) value, e>18, is ((19, 20, 21,..., 44), 24). The respective numbers of (e, m) values are 10906, 22762, 38655, 54574, 67352, 74311, 74026, 68070, 58847, 48066, 37270, 27551, 20015, 14180, 9574, 6470, 4372, 2461, 1671, 849, 549, 349, 124, 53, 17, and 41. For a Weibull probability fit of the data, the scaling parameter is 8.5791 with a 95% confidence interval of (8.5693, 8.5888) and the shaping parameter is 2.2626 with a 95% confidence interval of (2.2584, 2.2669). A histogram of the data with the Weibull probability distribution is;
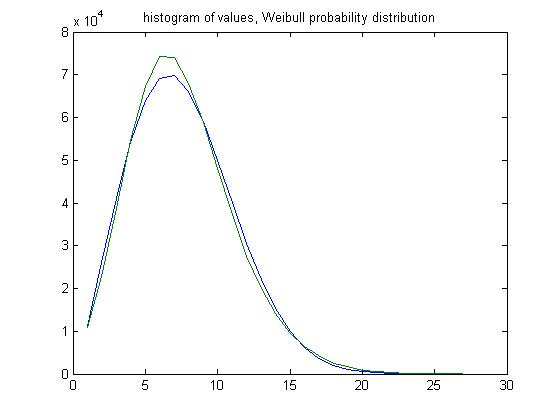
In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((21, 20), 30). For c=1, odd integers divisible by 3 less than or equal to 99999999, six primary attachment points, and m =30, the (e, m) value, e>21, is ((22, 23, 24,..., 50), 30). The respective numbers of (e, m) values are 1161, 20218, 29855, 37877, 42860, 44403, 42965, 38180, 32127, 25698, 19930, 14807, 10711, 7449, 5276, 3664, 2152, 1221, 669, 420, 309, 122, 84, 32, 18, 4, 1, 1, and 1. For a Weibull probability fit of the data, the scaling parameter is 8.0456 with a 95% confidence interval of (8.0329, 8.0583) and the shaping parameter is 2.0839 with a 95% confidence interval of (2.0789, 2.0890). A histogram of the data with the Weibull probability distribution is;
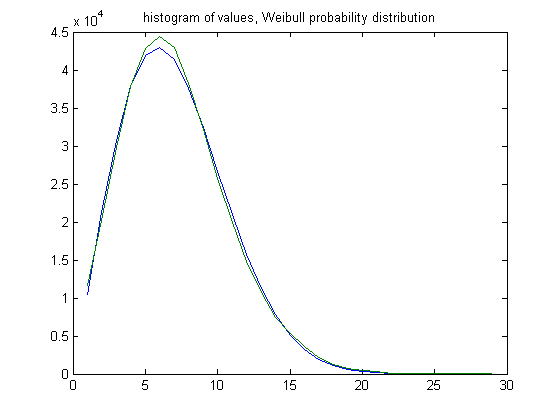
In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((25, 24), 36). For c=1, odd integers divisible by 3 less than or equal to 99999999, six primary attachment points, and m =36, the (e, m) value, e>25, is ((26, 27, 28,..., 49), 36). The respective numbers of (e, m) values are 12127, 16360, 19137, 21000, 20789, 19180, 16707, 13797, 10781, 8116, 6118, 4472, 3161, 2086, 1467, 1007, 777, 399, 230, 133, 83, 42, 23, and 8. For a Weibull probability fit of the data, the scaling parameter is 6.7759 with a 95% confidence interval of (6.7573, 6.7946) and the shaping parameter is 1.7813 with a 95% confidence interval of (1.7749, 1.7877). A histogram of the data with the Weibull probability distribution is;

In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((28, 27), 42). For c=1, odd integers divisible by 3 less than or equal to 99999999, six primary attachment points, and m =42, the (e, m) value, e>28, is ((29, 30, 31,..., 56), 42). The respective numbers of (e, m) values are 5981, 7402, 8325, 8552, 8136, 7418, 6238, 5093, 3930, 2891, 2241, 1495, 1117, 804, 561, 360, 226, 135, 76, 49, 20, 18, 9, 6, 1, 1, 0, and 1. For a Weibull probability fit of the data, the scaling parameter is 6.4243 with a 95% confidence interval of (6.3951, 6.4535) and the shaping parameter is 1.7068 with a 95% confidence interval of (1.6972, 1.7166). A histogram of the data with the Weibull probability distribution is;
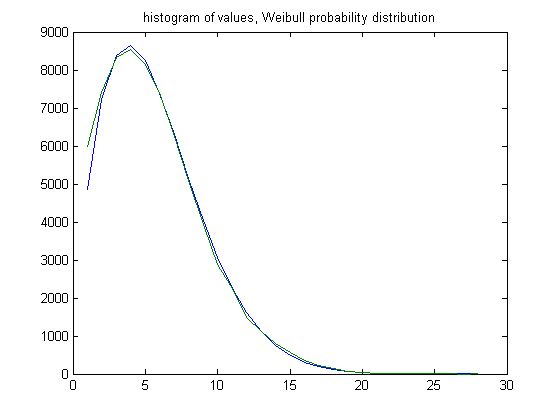
In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((32, 31), 48). For c=1, odd integers divisible by 3 less than or equal to 99999999, six primary attachment points, and m =48, the (e, m) value, e>32, is ((33, 34, 35,..., 59), 48). The respective numbers of (e, m) values are 2867, 3270, 3034, 2883, 2539, 2180, 1642, 1239, 962, 666, 460, 366, 225, 154, 102, 59, 48, 25, 19, 7, 4, 1, 1, 2, 0, 1, and 1. For a Weibull probability fit of the data, the scaling parameter is 5.4844 with a 95% confidence interval of (5.4371, 5.5321) and the shaping parameter is 1.5841 with a 95% confidence interval of (1.5684, 1.6000). A histogram of the data with the Weibull probability distribution is;
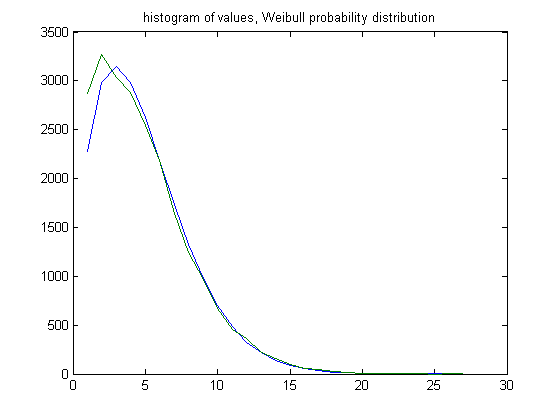
In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((35, 34), 54). For c=1, odd integers divisible by 3 less than or equal to 99999999, six primary attachment points, and m =54, the (e, m) value, e>35, is ((36, 37, 38,..., 58), 54). The respective numbers of (e, m) values are 1008, 1050, 1067, 949, 826, 667, 525, 382, 288, 199, 126, 85, 72, 43, 28, 18, 10, 8, 9, 1, 2, 1, and 1. For a Weibull probability fit of the data, the scaling parameter is 5.2841 with a 95% confidence interval of (5.2037, 5.3658) and the shaping parameter is 1.5735 with a 95% confidence interval of (1.5463, 1.6012). A histogram of the data with the Weibull probability distribution is;
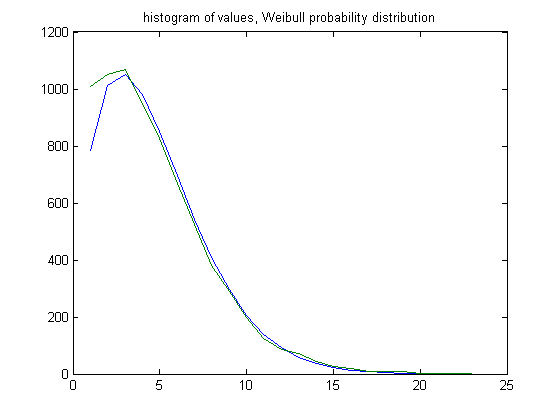
A plot of the logarithms of the histogram values is;
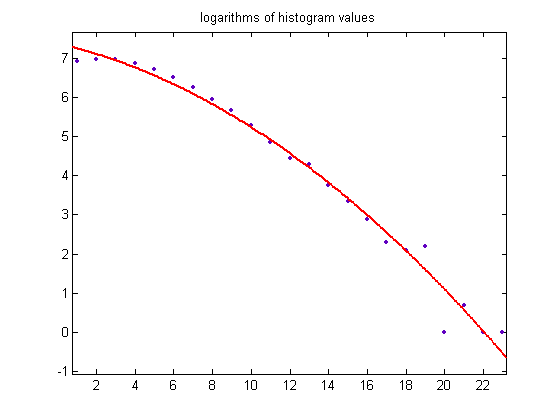
For a quadratic least-squares fit of the data, p1=-0.01004 with a 95% confidence interval of (-0.01375, -0.006341), p2=-0.1125 with a 95% confidence interval of (-0.204, -0.02096), p3=7.364 with a 95% confidence interval of (6.887, 7.841), SSE=2.233, R-squared=0.9821, and RMSE=0.3341.
Some of the best Weibull probability fits of the distributions are for m=35 through 41.
Generalized Dead Limbs with Eight Primary Attachment Points
In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((18, 17), 25). For c=1, odd integers divisible by 3 less than or equal to 99999999, eight primary attachment points, and m =25, the (e, m) value, e>18, is ((19, 20, 21,..., 46), 25). The respective numbers of (e, m) values are 31, 192, 831, 2683, 6599, 12880, 21933, 32106, 42274, 51286, 56370, 57003, 54074, 49346, 43031, 35975, 27471, 19936, 13368, 8669, 6174, 3741, 3483, 2518, 779, 197, 58, and 11. For a Weibull probability fit of the data, the scaling parameter is 14.0100 with a 95% confidence interval of (13.9989, 14.0211) and the shaping parameter is 3.5236 with a 95% confidence interval of (3.5166, 3.5305). A histogram of the data with the Weibull probability distribution is;
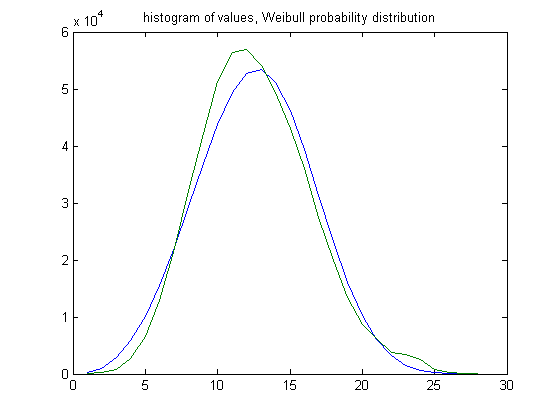
In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((21, 20), 30). For c=1, odd integers divisible by 3 less than or equal to 99999999, eight primary attachment points, and m =30, the (e, m) value, e>21, is ((22, 23, 24,..., 50), 30). The respective numbers of (e, m) values are 417, 1486, 3986, 8663, 16007, 24699, 35258, 44967, 52608, 57345, 58353, 56493, 51361, 43892, 36989, 30540, 21330 15267, 9917, 6383, 4671, 2454, 1734, 1201, 412, 193, 42, 12, and 6. For a Weibull probability fit of the data, the scaling parameter is 12.8853 with a 95% confidence interval of (12.8743, 12.8963) and the shaping parameter is 3.1607 with a 95% confidence interval of (3.1546, 3.1669). A histogram of data with the Weibull probability distribution is;
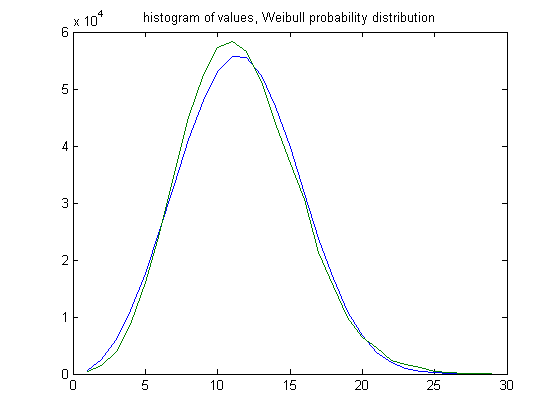
In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((24, 23), 35). For c=1, odd integers divisible by 3 less than or equal to 99999999, eight primary attachment points, and m =35, the (e, m) value, e>24, is ((25, 26, 27,..., 48), 35). The respective numbers of (e, m) values are 1590, 3832, 7850, 14024, 21083, 29015, 40003, 35543, 29765, 24653, 19616, 13632, 9217, 6126, 3898, 2848, 1442, 687, 493, 211, 80, 35, 9, and 2. For a Weibull probability fit of the data, the scaling parameter is 11.8853 with a 95% confidence interval of (11.8727, 11.8980) and the shaping parameter is 2.8047 with a 95% confidence interval of (2.7986, 2.8109). A histogram of the data with the Weibull probability distribution is;
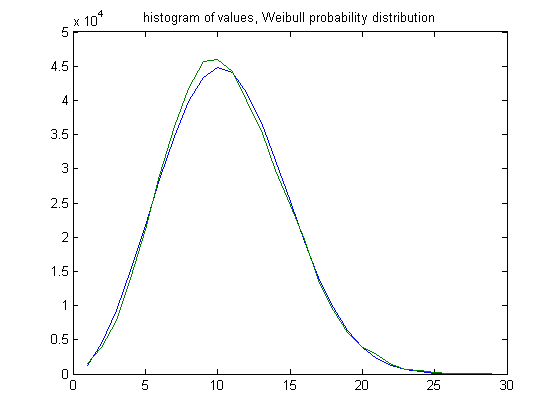
In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((27, 26), 40). For c=1, odd integers divisible by 3 less than or equal to 99999999, eight primary attachment points, and m =40, the (e, m) value, e>27, is ((28, 29, 30,..., 55), 40). The respective numbers of (e, m) values are 2954, 5739, 9673, 14322, 19609, 24408, 27902, 29741, 29955, 28843, 26756, 23582, 20166, 16812, 14626, 10879, 7543, 4980, 3083, 1920, 1428, 775, 385, 230, 115, 60, 21, and 3. For a Weibull probability fit of the data, the scaling parameter is 10.9974 with a 95% confidence interval of (10.9814, 11.0134) and the shaping parameter is 2.4825 with a 95% confidence interval of (2.4759, 2.4892). A histogram of the data with the Weibull probability distribution is;
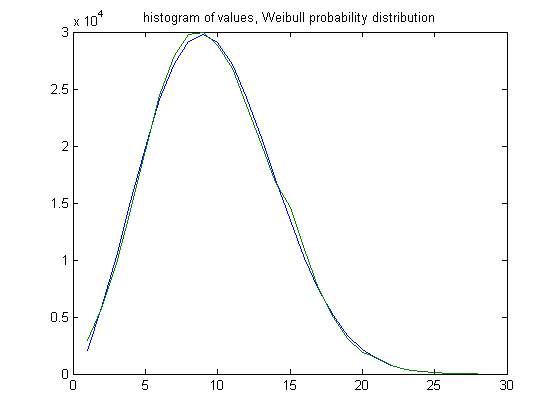
In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((30, 29), 45). For c=1, odd integers divisible by 3 less than or equal to 99999999, eight primary attachment points, and m =45, the (e, m) value, e>30, is ((31, 32, 33,..., 58), 45). The respective numbers of (e, m) values are 3562, 5891, 8708, 11695, 14151, 16278, 17295, 17218, 16229, 15505, 13857, 11819, 10237, 8585, 7420, 5590, 3604, 2438, 1432, 887, 647, 394, 204, 104, 41, 32, 11, 2, and 2. For a Weibull probability fit of the data, the scaling parameter is 10.1723 with a 95% confidence interval of (10.1507, 10.1939) and the shaping parameter is 2.2069 with a 95% confidence interval of (2.1992, 2.2147). A histogram of the data with the Weibull probability distribution is;
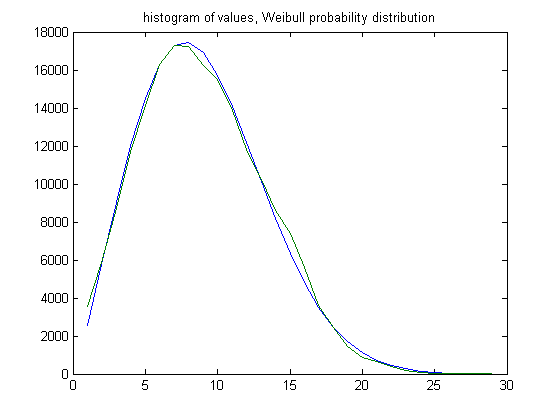
In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((33, 32), 50). For c=1, odd integers divisible by 3 less than or equal to 99999999, eight primary attachment points, and m =50, the (e, m) value, e>33, is ((34, 35, 36,..., 61), 50). The respective numbers of (e, m) values are 3226, 4588, 5979, 7235, 8383, 9007, 9090, 8593, 7967, 6994, 6049, 5334, 4346, 3709, 3292, 2338, 1649, 905, 522, 333, 250, 127, 96, 50, 22, 14, 2, and 1. For a Weibull probability fit of the data, the scaling parameter is 9.3360 with a 95% confidence interval of (9.3055, 9.3665) and the shaping parameter is 1.9950 with a 95% confidence interval of (1.9853, 2.0048). A histogram of the data with the Weibull probability distribution is;

In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((36, 35), 55). For c=1, odd integers divisible by 3 less than or equal to 99999999, eight primary attachment points, and m =55, the (e, m) value, e>36, is ((37, 38, 39,..., 66), 55). The respective numbers of (e, m) values are 2135, 2937, 3632, 3919, 4261, 4472, 4125, 3831, 3379, 2818, 2434, 1969, 1709, 1311, 1137, 830, 588, 355, 200, 122 ,74, 40, 29, 16, 10, 1, 2, 0, 1, and 1. For a Weibull probability fit of the data, the scaling parameter is 8.4738 with a 95% confidence interval of (8.4296, 8.5182) and the shaping parameter is 1.8345 with a 95% confidence interval of (1.8214, 1.8476). A histogram of the data with the Weibull probability distribution is;
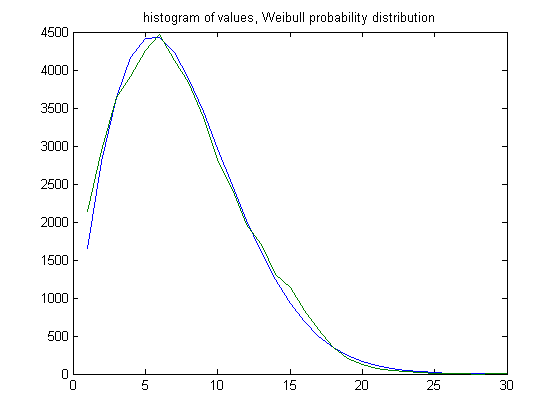
In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((39, 38), 60). For c=1, odd integers divisible by 3 less than or equal to 99999999, eight primary attachment points, and m =60, the (e, m) value, e>39, is ((40, 41, 42,..., 66), 60). The respective numbers of (e, m) values are 1229, 1558, 1757, 1912, 1964, 1830, 1726, 1547, 1317, 1101, 831, 693, 592, 434, 316, 230, 165, 94, 73, 35, 26, 21, 11, 6, 3, 1, and 1. For a Weibull probability fit of the data, the scaling parameter is 7.6835 with a 95% confidence interval of (7.6181, 7.7495) and the shaping parameter is 1.7312 with a 95% confidence interval of (1.7123, 1.7503). A histogram of the data with the Weibull probability distribution is;
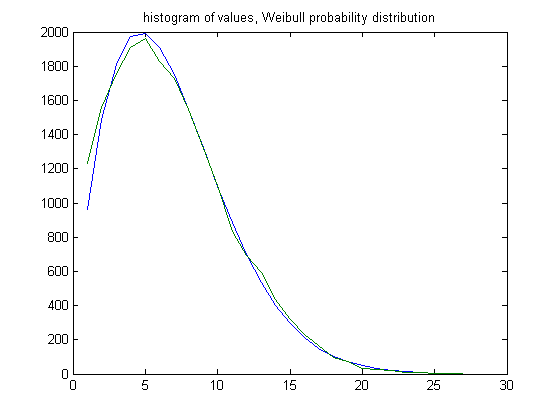
In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((42, 41), 65). For c=1, odd integers divisible by 3 less than or equal to 99999999, eight primary attachment points, and m =65, the (e, m) value, e>42, is ((43, 44, 45,..., 68), 65). The respective numbers of (e, m) values are 647, 784, 791, 841, 800, 780, 638, 553, 466, 387, 280, 224, 171, 138, 102, 48, 45, 35, 16, 13, 6, 3, 3, 2, 3, and 1. For a Weibull probability fit of the data, the shaping parameter is 6.9415 with a 95% confidence interval of (6.8432, 7.0412) and the shaping parameter is 1.6439 with a 95% confidence interval of (1.6157, 1.6725). A histogram of the data with the Weibull probability distribution is;

In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((44, 43), 70). For c=1, odd integers divisible by 3 less than or equal to 99999999, eight primary attachment points, and m =70, the (e, m) value, e>44, is ((45, 46, 47,..., 68), 70). The respective numbers of (e, m) values are 279, 325, 358, 357, 338, 332, 288, 231, 212, 149, 128, 83, 69, 51, 41, 37, 20, 10, 12, 5, 3, 1, and 3. For a Weibull probability fit of the data, the scaling parameter is 6.9273 with a 95% confidence interval of (6.7778, 7.0802) and the shaping parameter is 1.6413 with a 95% confidence interval of (1.5986, 1.6851). A histogram of the data with the Weibull probability distribution is;
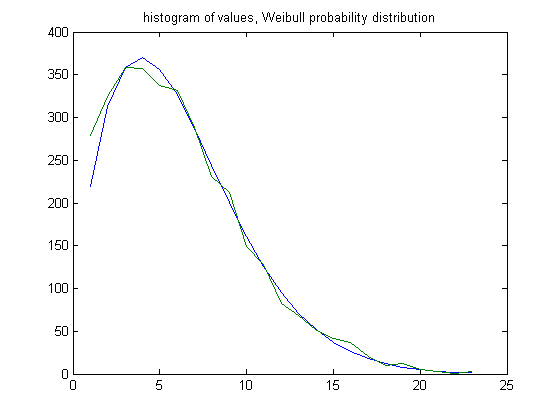
In the original definition of generalized dead limbs and for c=1 or -1, an (e, m) value is ((47, 46), 75). For c=1, odd integers divisible by 3 less than or equal to 99999999, eight primary attachment points, and m =75, the (e, m) value, e>47, is ((48, 49, 50,..., 71), 75). The respective numbers of (e, m) values are 155, 146, 157, 172, 157, 112, 95, 65, 76, 54, 50, 33, 30, 15, 4, 8, 12, 4, 5, 1, 0, 1, 0, and 1. For a Weibull probability fit of the data, the scaling parameter is 6.2982 with a 95% confidence interval of (6.0720, 6.5328) and the shaping parameter is 1.5388 with a 95% confidence interval of (1.4768, 1.6032). A histogram of the data with the Weibull probability distribution is;
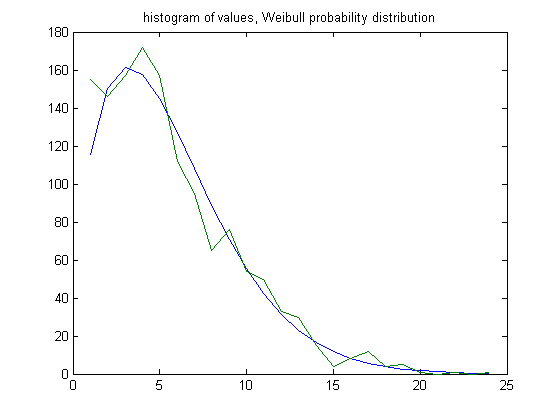
A plot of the logarithms of the histogram values is;
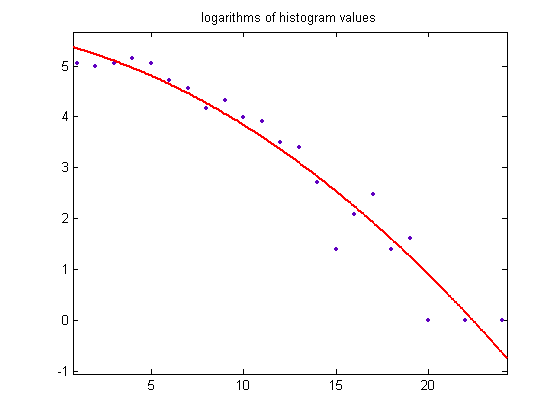
For a quadratic least-squares fit of the data, p1=-0.006695 with a 95% confidence interval of (-0.01141, -0.00198), p2=-0.0931 with a 95% confidence interval of (-0.2102, 0.024), p3=5.439 with a 95% confidence interval of (4,819, 6.06), SSE=3.675, R-squared=0.9449, and RMSE=0.4398.
A plot of the Weibull scaling parameters for m=8 through 90 is;
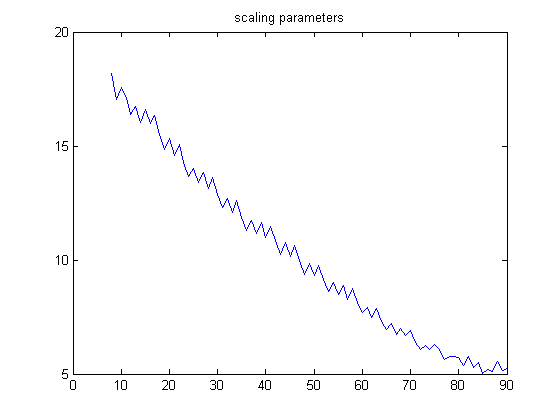
For a quadratic least-squares fit of the data, p1=0.00107 with a 95% confidence interval of (0.0009409, 0.001198), p2=-0.2627 with a 95% confidence interval of (-0.2756, -0.2498), p3=19.87 with a 95% confidence interval of (19.59, 20.15), SSE=7.32, R-squared=0.994, and RMSE=0.3025. A plot of the fit is;
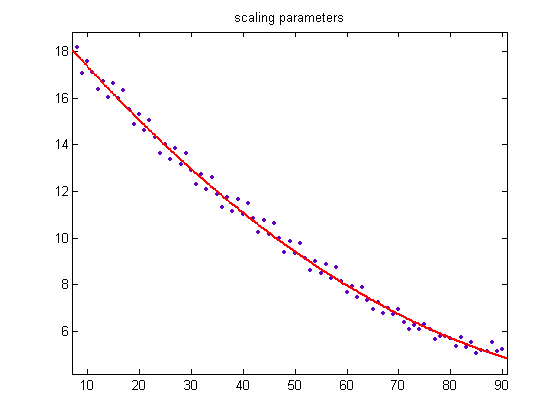
A plot of the shaping parameters is;

For a quadratic least-squares fit of the data, p1=0.0007334 with a 95% confidence interval of (0.0006984, 0.0007683), p2=-0.1133 with a 95% confidence interval of (-0.1168, -0.1098), p3=5.884 with a 95% confidence interval of (5.809, 5.96), SSE=0.5385, R-squared=0.9943, and RMSE=0.08205. A plot of the fit is;

The Number of Generalized Dead Limbs for 3n+c Cycles with Various Numbers of Attachment Points
As previously discussed, the attachment points for the known 3n+5 cycles are 2, 38, 1562, 1496, 374, 1436, and 1334 (some of these attachment points may be in the same cycle). A table of the respective numbers of generalized dead limbs containing the entire cycle or portions of it (determined using the attachment points) for different numbers (1, 2, and 3) of primary attachment points in the generalized dead limbs for odd integers divisible by 3 less than or equal to 99999999 is;
c=-1, cycle attachment points: 68 1 a. p. 1 2 a. p. 74 3 a. p. 603 c=5, cycle attachment points: 2 38 ([1562 1496 374*] [1436 1334]) 1 a. p. 1 1 1 1 0 0 1 2 a. p. 10 54 79 30 22 70 67 3 a. p. 74 453 438 271 121 432 459 c=7, cycle attachment points: 10 1 a. p. 1 2 a. p. 26 3 a. p. 340 c=11, cycle attachment points: [8 2*] [62 26] 1 a. p. 1 0 1 1 2 a. p. 21 2 67 25 3 a. p. 132 0 747 336 c=13, cycle attachment points: 4 (454 502 574 682 844) [1048 262* 358] 1 a. p. 1 1 1 1 1 1 1 1 1 2 a. p. 8 35 39 46 54 63 123 0 38 3 a. p. 97 177 242 334 318 422 771 0 387 c=17, cycle attachment points: [8 2*] [140 50 62] 1 a. p. 1 1 1 1 1 2 a. p. 19 0 72 34 64 3 a. p. 162 0 627 363 556 c=-17, cycle attachment points: 130 1 a. p. 1 2 a. p. 62 3 a. p 477 c=19, cycle attachment points: [28 10] 1 a. p. 1 1 2 a. p. 36 9 3 a. p. 255 123 c=-19, cycle attachment points: [374 230] 1 a. p. 1 1 2 a. p. 43 83 3 a. p. 353 518 c=23, cycle attachment points: (14 20) [1244 392 98* 110] 1 a. p. 1 1 1 1 1 1 2 a. p. 17 16 158 66 0 35 3 a. p. 226 130 1035 662 0 346 c=-23, cycle attachment points: ([11878 7486] 7330 [23704 5926* 12526] [19330 8134] [14686 12364] 9436 9052) 1 a. p. 1 1 1 1 0 1 1 1 1 1 0 0 2 a. p. 47 39 58 49 27 38 54 45 66 25 58 65 3 a. p. 269 246 279 221 136 198 272 283 323 206 249 295 c=25, cycle attachment points: 34 [88 22* 28] 1 a. p. 1 0 1 1 2 a. p. 29 53 0 20 3 a. p. 407 462 0 186 c=-25, cycle attachment points: [1502 452 242] 1 a. p. 1 1 1 2 a. p. 94 32 41 3 a. p. 618 301 316 c=29, cycle attachment points: [176 44*] [8 2*] ([788552 197138* 194366 79082 73934 41606 18794] [1707830 1441016 360254* 577232 144308* 36902 20306 7622]) 1 a. p. 1 1 1 0 1 1 0 1 1 1 0 1 1 0 1 1 0 0 1 2 a. p. 76 16 11 0 40 3 56 30 4 19 47 67 16 8 26 14 54 10 4 3 a. p. 699 163 96 0 204 14 291 127 45 79 174 271 101 34 92 45 253 50 25 c=-29, cycle attachment points: 226 1 a. p. 1 2 a. p. 62 3 a. p. 460 c=31, cycle attachment points: [106 58 52 34] 1 a. p. 1 1 1 1 2 a. p. 44 55 19 30 3 a. p. 435 483 167 249 c=-31, cycle attachment points: 380 1 a. p. 1 2 a. p. 85 3 a. p. 543
c=35, cycle attachment points: (68 [104 26*]) 1 a.p. 1 1 0 2 a.p. 38 34 28 3 a.p. 287 217 250 c=37, cycle attachment points: (46 58 76) 1 a.p. 0 1 1 2 a.p. 26 37 38 3 a.p. 190 234 381 c=41, cycle attachment points: [128 32* 8 2] 38 1 a.p. 1 1 1 1 0 2 a.p. 39 19 0 1 27 3 a.p. 318 179 0 0 295 c=43, cycle attachment points: [28 16 4*] 1 a.p. 1 1 1 2 a.p. 19 10 0 3 a.p. 159 80 0 c=47, cycle attachment points: (170 206 260) [44 20 38 26] [494 200 50* 98] 1 a.p. 1 1 1 0 1 1 1 1 1 1 1 2 a.p. 35 45 54 20 8 26 8 87 37 0 37 3 a.p. 265 362 481 166 97 195 86 561 279 0 262 c=49, cycle attachment points: [814 400 100* 178] 1 a.p. 1 1 1 1 2 a.p. 84 55 0 57 3 a.p. 620 402 0 482 c=-119, cycle attachment points: 622 1 a.p. 0 2 a.p. 91 3 a.p. 499 c=175, cycle attachment points: (412 [358 178] 292 286 202) [664 166* 106] [1222 502 232 58* 142] 1 a.p. 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 a.p. 44 35 23 26 32 33 47 6 7 60 21 16 6 10 3 a.p. 412 279 178 189 302 203 338 95 92 365 220 221 58 114 c=221, cycle attachment points: [320 80* 20 362] 1 a.p. 1 1 1 1 2 a.p. 32 0 0 37 3 a.p. 299 0 0 252 c=461, cycle attachment points: [200 50* 134 1106 530 314 290 224 56* 16 296 74*] 1 a.p. 1 1 0 1 1 1 1 1 0 1 0 1 2 a.p. 8 0 14 25 25 15 15 7 1 0 19 2 3 a.p. 76 0 44 145 132 152 94 71 0 0 94 0
The parentheses denote interrelated cycles, the brackets denote the attachments within a cycle, and the asterisks denote secondary attachment points. The number of generalized dead limbs containing a secondary attachment point usually does not increase as rapidly as for primary cycle attachment points
A plot of the number of generalized dead limbs containing the c=-1 cycle or a portion of it when the number of odd integers divisible by 3 is less than or equal to 9999999 versus the number of primary attachment points in the generalized dead limbs is;
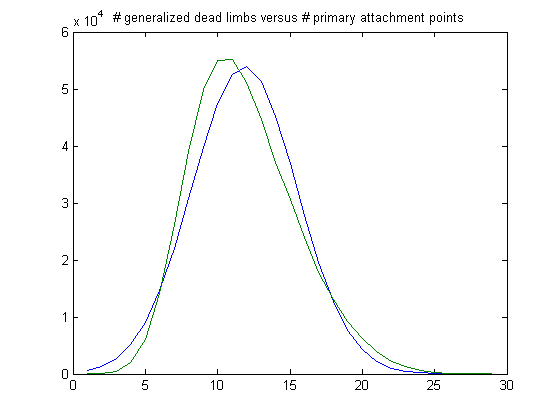
The sample size is 489621 and the largest value is 29. For a normal probability fit of the data, the mean is 11.8390 with a 95% confidence interval of (11.8288, 11.8491) and the standard deviation is 3.6188 with a 95% confidence interval of (3.6117, 3.6260). In the above plot, the actual data is skewed to the left.
A plot of the number of generalized dead limbs containing the c=5 cycles or portions of them when the number of odd integers divisible by 3 is less than or equal to 9999999 versus the number of primary attachment points in the generalized dead limbs is;
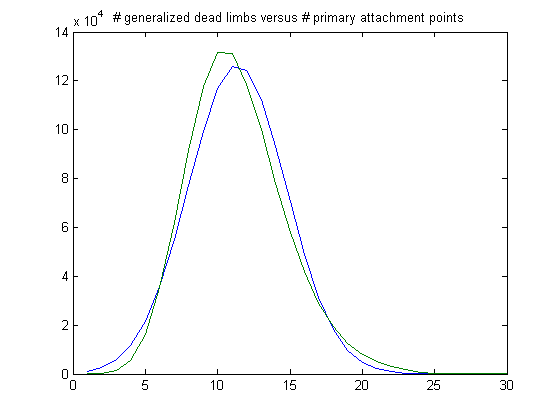
The sample size is 1069700 and the largest value is 30. For a normal probability fit of the data, the mean is 11.35779 with a 95% confidence interval of (11.3515, 11.3643) and the standard deviation is 3.3726 with a 95% confidence interval of (3.3681, 3.3771).
A plot of the number of generalized dead limbs containing the c=7 cycle or a portion of it when the number of odd integers divisible by 3 is less than or equal to 9999999 versus the number of primary attachment points in the generalized dead limbs is;

The sample size is 1202551 and the largest value is 30. For a normal probability fit of the data, the mean is 13.0050 with a 95% confidence interval of (12.9987, 13.0113) and the standard deviation is 3.5103 with a 95% confidence interval of (3.5059, 3.5148).
A plot of the number of generalized dead limbs containing the c=11 cycles or portions of them when the number of odd integers divisible by 3 is less than or equal to 3999999 versus the number of primary attachment points in the generalized dead limbs is;
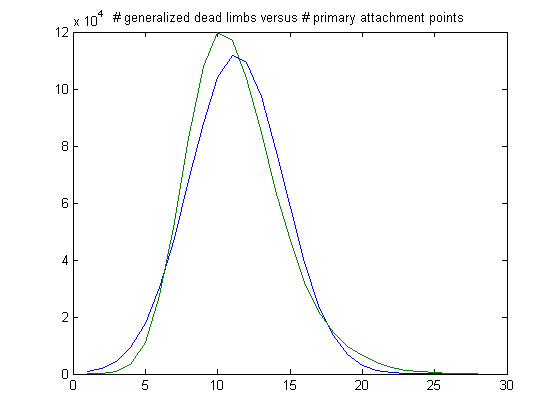
The sample size is 916791 and the largest value is 28. For a normal probability fit of the data, the mean is 11.2743 with a 95% confidence interval of (11.2676, 11.2809) and the standard deviation is 3.2605 with a 95% confidence interval of (3.2558, 3.2652).
A plot of the number of generalized dead limbs containing the c=13 cycles or portions of them when the number of odd integers divisible by 3 is less than or equal to 3999999 versus the number of primary attachment points in the generalized dead limbs is;

The sample size is 684366 and the largest value is 28. For a normal probability fit of the data, the mean is 11.0505 with a 95% confidence interval of (11.0426, 11.0583) and the standard deviation is 3.3025 with a 95% confidence interval of (3.2970, 3.3081).
A plot of the number of generalized dead limbs containing the c=17 cycles or portions of them when the number of odd integers divisible by 3 is less than or equal to 3999999 versus the number of primary attachment points in the generalized dead limbs is;

The sample size is 1223672 and the largest value is 28. For a normal probability fit of the data, the mean is 11.2171 with a 95% confidence interval of (11.2115, 11.2227) and the standard deviation is 3.1640 with a 95% confidence interval of (3.1601, 3.1680).
A plot of the number of generalized dead limbs containing the c=-17 cycle or a portion of it when the number of odd integers divisible by 3 is less than or equal to 9999999 versus the number of primary attachment points in the generalized dead limbs is;
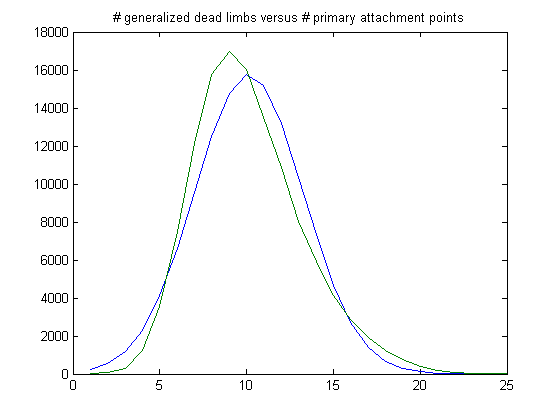
The sample size is 123603 and the largest value is 25. For a normal probability fit of the data, the mean is 10.1271 with a 95% confidence interval of (10.1097, 10.1445) and the standard deviation is 3.1255 with a 95% confidence interval of (3.1133, 3.1379).
A plot of the number of generalized dead limbs containing the c=19 cycles or portions of them when the number of odd integers divisible by 3 is less than or equal to 3999999 versus the number of primary attachment points in the generalized dead limbs is;
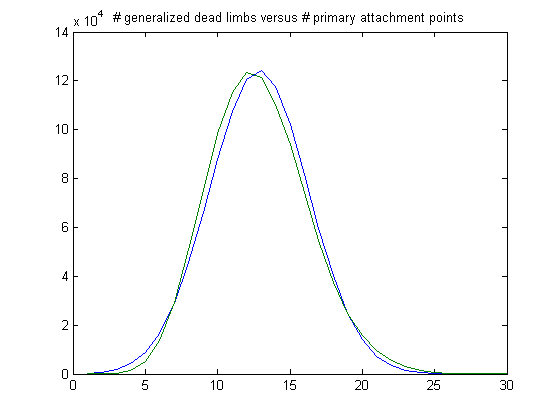
The sample size is 1066731 and the largest value is 30. For a normal probability fit of the data, the mean is 12.8548 with a 95% confidence interval of (12.8483, 12.8613) and the standard deviation is 3.4230 with a 95% confidence interval of (3.4184, 3.4276).
A plot of the number of generalized dead limbs containing the c=-19 cycles or portions of them when the number of odd integers divisible by 3 is less than or equal to 9999999 versus the number of primary attachment points in the generalized dead limbs is;
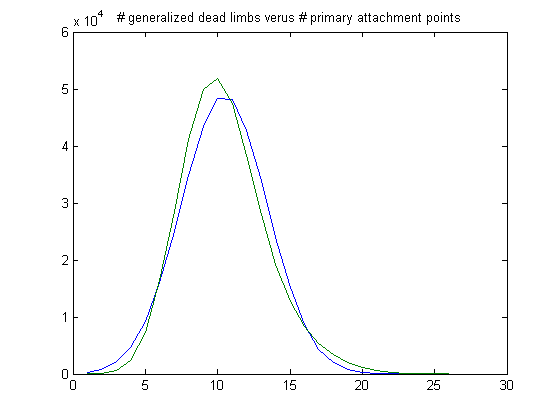
The sample size is 364984 and the largest value is 26. For a normal probability fit of the data, the mean is 10.4516 with a 95% confidence interval of (10.4420, 10.4613) and the standard deviation is 2.9758 with a 95% confidence interval of (2.9690, 2.9826).
A plot of the number of generalized dead limbs containing the c=23 cycles or portions of them when the number of odd integers divisible by 3 is less than or equal to 3999999 versus the number of primary attachment points in the generalized dead limbs is;
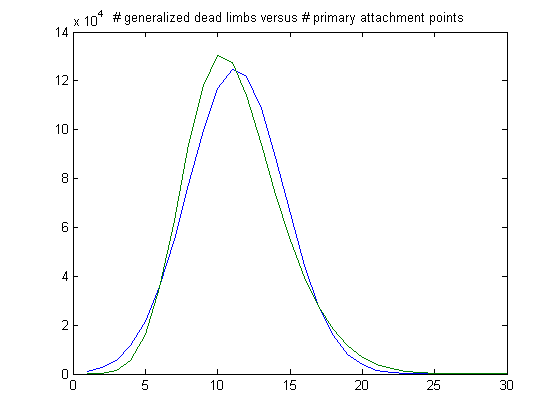
The sample size is 1039654 and the maximum value is 30. For a normal probability fit of the data, the mean is 11.2383 with a 95% confidence interval of (11.2319, 11.2447) and the standard deviation is 3.3140 with a 95% confidence interval of (3.3101, 3.3191).
A plot of the number of generalized dead limbs containing the c=-23 cycles or portions of them when the number of odd integers divisible by 3 is less than or equal to 9999999 versus the number of primary attachment points in the generalized dead limbs is;
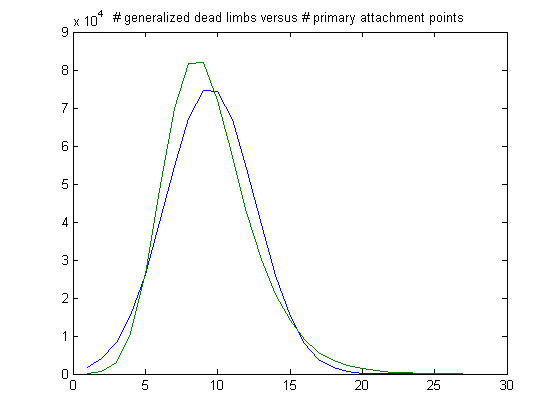
The sample size is 583261 and the largest value is 27. For a normal probability fit of the data, the mean is 9.4843 with a 95% confidence interval of (9.4764, 9.4923) and the standard deviation is 3.0833 with a 95% confidence interval of ( 3.0777, 3.0889).
A plot of the number of generalized dead limbs containing the c=25 cycles or portions of them when the number of odd integers divisible by 3 is less than or equal to 999999 versus the number of primary attachment points in the generalized dead limbs is;
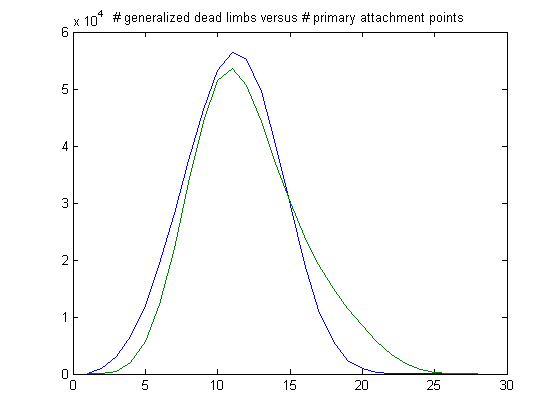
The sample size is 478156 and the largest value is 28. For a normal probability fit of the data, the mean is 12.1917 with a 95% confidence interval of (12.1810, 12.2024) and the standard deviation is 3.7749 with a 95% confidence interval of (3.7673, 3.7824).
A plot of the number of generalized dead limbs containing the c=-25 cycles or portions of them when the number of odd integers divisible by 3 is less than or equal to 9999999 versus the number of primary attachment points in the generalized dead limbs is;
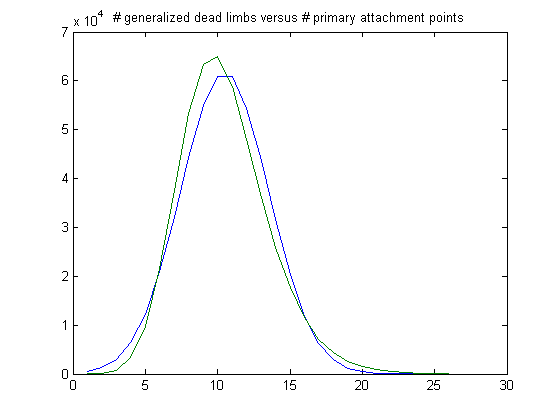
The sample size is 470456 and the largest value is 26. For a normal probability fit of the data, the mean is 10.4747 with a 95% confidence interval of (10.4660, 10.4834) and the standard deviation is 3.0416 with a 95% confidence interval of (3.0354, 3.0477).
A plot of the number of generalized dead limbs containing the c=-119 cycle or a portion of it when the number of odd integers divisible by 3 is less than or equal to 9999999 versus the number of primary attachment points in the generalized dead limbs is;
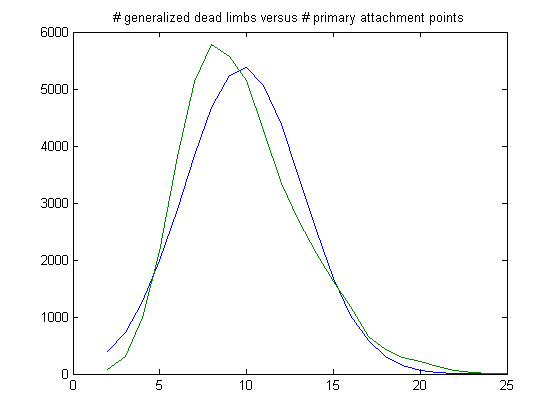
The sample size is 45997 and the largest value is 25. For a normal probability fit of the data, the mean is 9.8106 with a 95% confidence interval of (9.7705, 9.8328) and the standard deviation is 3.4105 with a 95% confidence interval of (3.3886, 3.4327).
A plot of the number of generalized dead limbs containing the c=175 cycles or portions of them when the number of odd integers divisible by 3 is less than or equal to 3999999 versus the number of primary attachment points in the generalized dead limbs is;
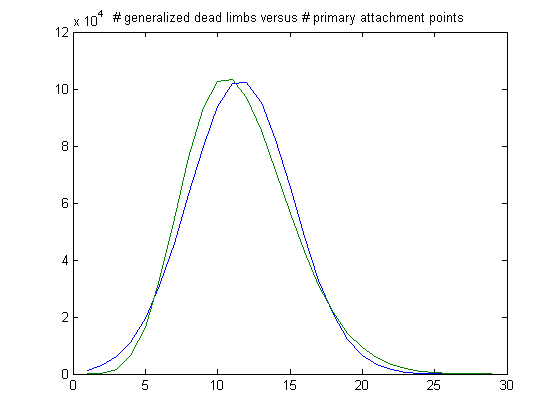
The sample size is 928904 and the largest value is 29. For a normal probability fit, the mean is 11.5746 with a 95% confidence interval of (11.5673, 11.5819) and the standard deviation is 3.5919 with a 95% confidence interval of (3.5868, 3.5971).
A plot of the number of generalized dead limbs containing the c=221 cycles or portions of them when the number of odd integers divisible by 3 is less than or equal to 3999999 versus the number of primary attachment points in the generalized dead limbs is;
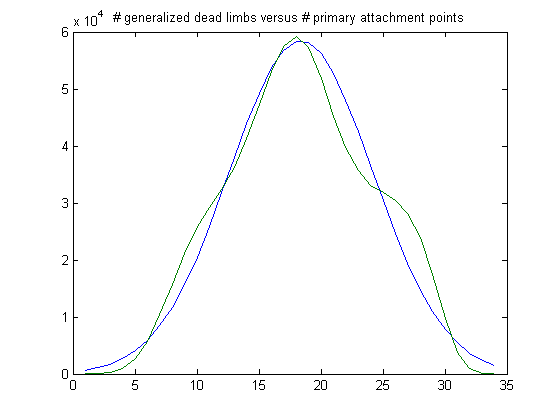
The sample size is 848161 and the largest value is 34. For a normal probability fit, the mean is 18.3817 with a 95% confidence interval of (18.3693, 18.3940) and the standard deviation is 5.7917 with a 95% confidence interval of (5.7830, 5.8005).
A plot of the number of generalized dead limbs containing the c=461 cycles or portions of them when the number of odd integers divisible by 3 is less than or equal to 999999 versus the number of primary attachment points in the generalized dead limbs is;
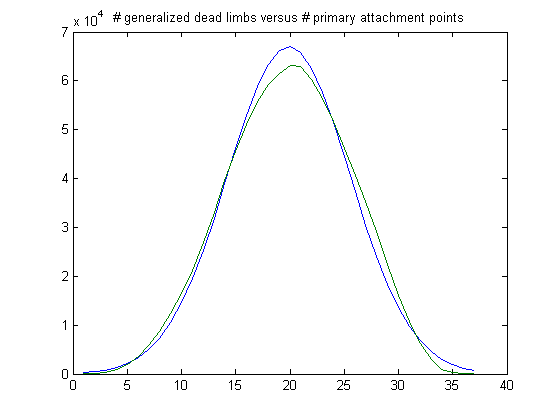
The sample size is 950302 and the largest value is 37. For a normal probability fit of the data, the mean is 19.8890 with a 95% confidence interval of (19.8776, 19.9003) and the standard deviation is 5.6552 with a 95% confidence interval of (5.6472, 5.6633).
The Number of Odd Integers Divisible by 3 Contained in Generalized Dead Limbs
Let d denote (U-U')/6 where U is the upper bound of the odd integers divisible by 3 and U'=U-6, U-12, U-18, ....(this is just a mapping from the odd integers divisible by 3 to the natural numbers). For an upper bound of 999 and a lower bound of 3 for the odd integers divisible by 3, a linear least-squares fit of the d values of the generalized dead limbs containing the c=-1 cycle or a portion of it is;
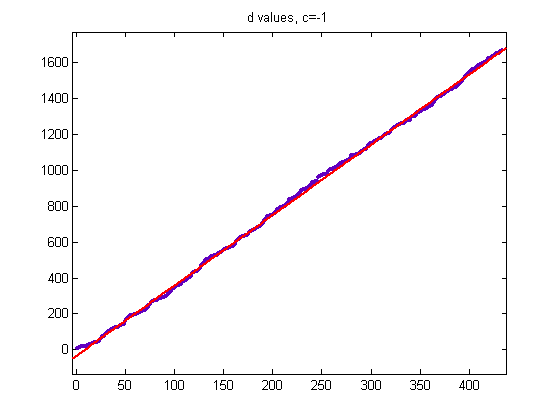
The slope is 3.921 with a 95% confidence interval of (3.912, 3.931), the intercept is -35.11 with a 95% confidence interval of (-37.44, -32.78), SSE=65500, R-squared=0.9994, and RMSE=12.31.
Six cycles for c=-1, 7, -17, -29, -31, and -119 use a large percentage of the odd integers divisible by 3. These cycles appear to be unique in that there are no other cycles for these c values and the cycles have only one attachment point apiece. For an upper bound of 99999999 for the odd integers divisible by 3 (and a lower bound of -819), the numbers of odd integers divisible by 3 that are covered by the generalized dead limbs 1, 2, 3, 4, 5, and 6 times are 8372669, 4684440, 831733, 64777, 2320, and 36 respectively. A plot of the logarithms of these values is;
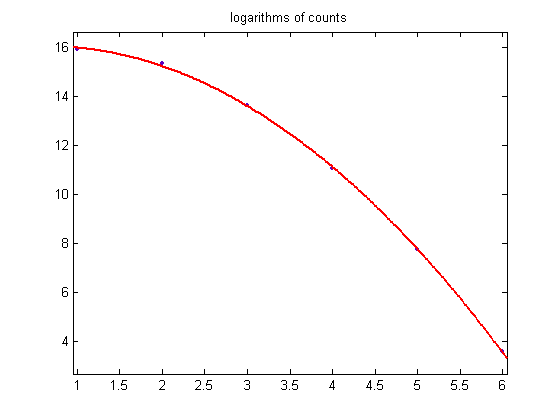
For a quadratic least-squares fit of the data, p1=-0.4344 with a 95% confidence interval of (-0.4784, -0.3905), p2=0.5506 with a 95% confidence interval of (0.2361, 0.8651), p3=15.89 with a 95% confidence interval of (15.41, 16.37), SSE=0.02139, R-squared=0.9998, and RMSE=0.08443. The number of odd integers divisible by 3 not used by any generalized dead limb is 2710829, so about 83.74% ((16666804-2710829)/16666804) of the odd integers divisible by 3 are covered. The numbers of odd integers divisible by 3 used by the generalized dead limbs of the c=-1, 7, -17, -29, -31, and -119 cycles individually are 4856981, 11912639, 1229913, 741308, 1313208, and 453623 respectively.
For an upper bound of 9999999 for the odd integers divisible by 3, the numbers of odd integers divisible by 3 that are covered by the generalized dead limbs 1, 2, 3, 4, 5, and 6 times are 837445, 474285, 84707, 6763, 232, and 3 respectively. A plot of the logarithms of these values is;
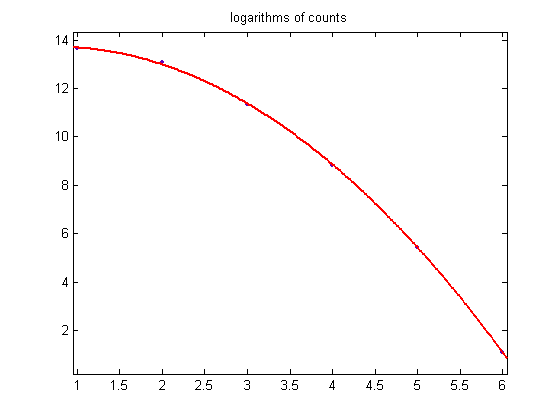
For a quadratic least-squares fit of the data, p1=-0.4553 with a 95% confidence interval of (-0.4881, -0.4225), p2=0.6702 with a 95% confidence interval of (0.4357, 0.9047), p3=13.46 with a 95% confidence interval of (13.1, 13.82), SSE=0.01189, R-squared=0.9999, and RMSE=0.06297. The number of odd integers divisible by 3 not used by any generalized dead limb is 263369, so about 84.20% ((1666804-263369)/1666804) of the odd integers divisible by 3 are covered. The numbers of odd integers divisible by 3 used by the generalized dead limbs of the c=-1, 7, -17, -29, -31, and -119 cycles individually are 489621, 1202551, 123603, 74168, 132426, and 45997 respectively.
For an upper bound of 999999 for the odd integers divisible by 3, the numbers of odd integers divisible by 3 that are covered by the generalized dead limbs for 1, 2, 3, 4, and 5 times are 83741, 48343, 8690, 717, and 24 respectively. A plot of the logarithms of these values is;

For a quadratic least-squares fit of the data, p1=-0.4624 with a 95% confidence interval of (-0.5467, -0.3782), p2=0.722 with a 95% confidence interval of (0.2067, 1.237), p3=11.11 with a 95% confidence interval of (10.43, 11.79), SSE=0.01074, R-squared=0.9998, and RMSE=0.07327. The number of odd integers divisible by 3 not used by any generalized dead limb is 25289, so about 84.84% ((166804-25289)/166804) of the odd integers divisible by 3 are covered. The numbers of odd integers divisible by 3 used by the generalized dead limbs of the c=-1, 7, -17, -29, -31, and -119 cycles individually are 49585, 121774, 12528, 7462, 13479, and 4657 respectively.
Generalized Dead Limbs for c=5 Cycles
For odd integers divisible by 3 less than or equal to 9999999 and greater than or equal to -819, a plot of the number of generalized dead limbs containing the c=5 cycle where (K+L, K)=(27, 17) and there are 3 cycle attachment points versus the number of primary attachment points (in the generalized dead limbs) is;
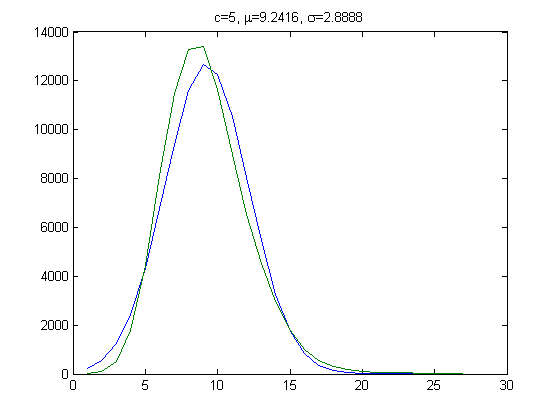
The mean of the normal probability distribution fit is 9.2416 with a 95% confidence interval of (9.2229, 9.2602) and the intercept is 2.8888 with a 95% confidence interval of (2.8757, 2.9027). The sample size is 92027 and the largest value is 27. For this cycle, two generalized dead limbs usually contain the same odd integer divisible by 3. (The path from the odd integer divisible by 3 to the cycle is deterministic, but different stopping points within the cycle are considered. There are 19 entry points into the cycle.) A linear least-squares fit of the d values contained in the generalized dead limbs where only one generalized dead limb contains an odd integer divisible by 3 is;
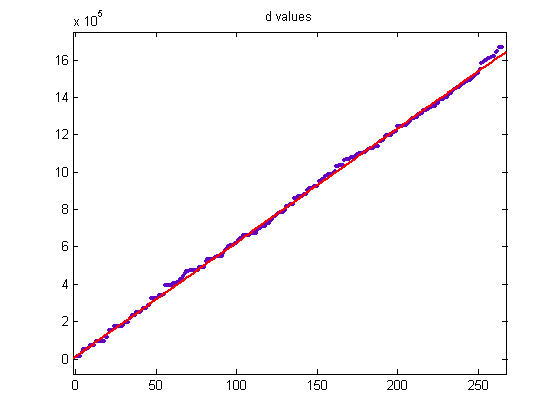
For a linear least-squares fit of the data, the slope is 6106 with a 95% confidence interval of (6083, 6129), the intercept is 13500 with a 95% confidence interval of (9958, 17050), SSE=5.613e+10, R-squared=0.9688, and RMSE=1.461e+4. The sample size is 265. A linear least-squares fit of the d values contained in the generalized dead limbs where two dead limbs contain the same odd integer divisible by 3 is;

For a linear least-squares fit of the data, the slope is 36.29 with a 95% confidence interval of (36.29, 36.29), the intercept is -843.5 with a 95% confidence interval of (-900.2, -786.7), SSE=4.405e+11, R-squared=1, and RMSE=3099..
For odd integers divisible by 3 less than or equal to 9999999 and greater than or equal to -819, a plot of the number of generalized dead limbs containing the c=5 cycle where (K+L, K)=(27, 17) and there are 2 cycle attachment points versus the number of primary attachment points (in the generalized dead limbs) is;
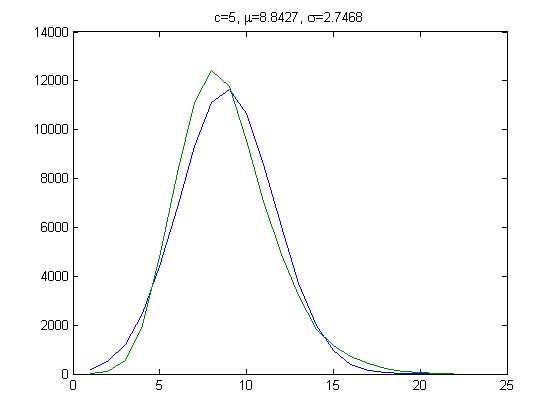
For a normal probability fit of the data, the mean is 8.8427 with a 95% confidence interval of (8.8237, 8.8617) and the standard deviation is 2.7468 with a 95% confidence interval of (2.7334, 2.7603). The sample size is 80280 and the largest value is 22. For this cycle, two generalized dead limbs usually contain the same odd integer divisible by 3. A linear least-squares fit of the d values contained in the generalized dead limbs where only one generalized dead limb contains an odd integer divisible by 3 is;
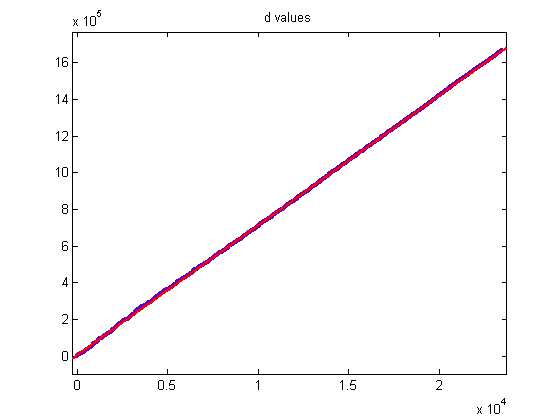
For a linear least-squares fit of the data, the slope is 70.71 with a 95% confidence interval of (70.7, 70.72), the intercept is 4011 with a 95% confidence interval of (3915, 4107), SSE=3.325e+11, R-squared=0.9999, and RMSE=3761. A linear least-squares fit of the d values contained in the generalized dead limbs where two dead limbs contain the same odd integer divisible by 3 is;
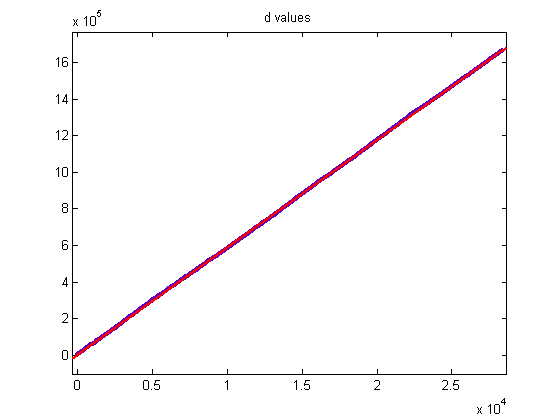
For a linear least-squares fit of the data, the slope is 58.78 with a 95% confidence interval of (58.78, 58.79), the intercept is -1663 with a 95% confidence interval of (-1733, -1593), SSE=2.588e+11, R-squared=1, and RMSE=3019.
For odd integers divisible by 3 less than or equal to 9999999 and greater than or equal to -819, a plot of the number of generalized dead limbs containing the c=5 cycle where (K+L, K)=(2, 1) versus the number of primary attachment points (in the generalized dead limbs) is;

For a normal probability fit of the data, the mean is 12.0087 with a 95% confidence interval of (11.9938, 12.0235) and the standard deviation is 3.3579 with a 95% confidence interval of (3.3474, 3.3684). The sample size is 197624 and the largest value is 28. A linear least-squares fit of the d values contained in the generalized dead limbs is;

For a linear least-squares fit of the data, the slope is 8.412 with a 95% confidence interval of (8.412, 8.412), the intercept is 6661 with a 95% confidence interval of (6640, 6683), SSE=1.174e+12, R-squared=1, and RMSE=2437.
For odd integers divisible by 3 less than or equal to 9999999 and greater than or equal to -819, a plot of the number of generalized dead limbs containing the c=5 cycle where (K+L, K)=(5, 3) versus the number of primary attachment points (in the generalized dead limbs) is;
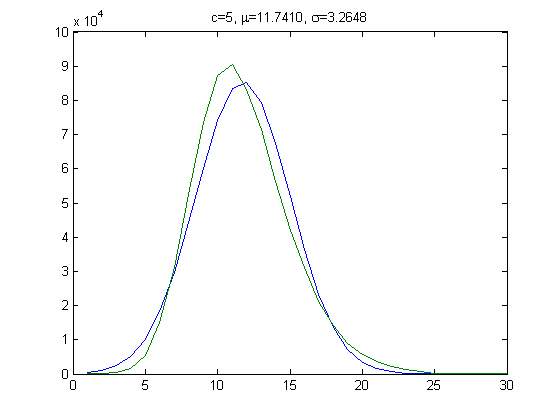
For a normal probability fit of the data, the mean is 11.7410 with a 95% confidence interval of (11.7333, 11.7486) and the standard deviation is 3.2648 with a 95% confidence interval of (3.2594, 3.2702). The sample size is 699769 and the largest value is 30. A linear least-squares fit of the d values contained in the generalized dead limbs is;

For a linear least-squares fit of the data, the slope is 2.374 with a 95% confidence interval of (2.734, 2.734), the intercept is 5307 with a 95% confidence interval of (5297, 5318), SSE=3.482e+12, R-squared=1, and RMSE=2231.
Using only the largest cycle attachment points reduces the number of generalized dead limbs that map to the same odd integer divisible by 3. A table of the reductions for various c values is;
| c=-1 1→1 |
| c=5 2→1 |
| c=7 1→1 |
| c=11 2→1 |
| c=13 4→2 |
| c=17 3→1 |
| c=-17 1→1 |
| c=19 2→1 |
| c=-19 3→2 |
| c=23 4→1 |
| c=-23 3→1 |
| c=25 6→5 |
| c=-25 3→1 |
| c=29 2→1 |
| c=-29 1→1 |
| c=31 4→1 |
| c=-31 1→1 |
| c=35 2→1 |
| c=37 1→1 |
| c=41 3→1 |
| c=43 3→1 |
| c=47 4→1 |
| c=49 4→1 |
| c=-119 1→1 |
| c=175 5→1 |
| c=221 3→1 |
| c=461 9→1 |
The numbers in the second column indicate the maximum number of generalized dead limbs that can map to the same odd integer divisible by 3 when all the cycle attachment points (of all the cycles) are used. The numbers in the third column indicate the maximum number of generalized dead limbs that can map to the same odd integer divisible by 3 when only the largest cycle attachment point (of a particular cycle) is used.
References
1) R. E. Crandall, On the "3x+1" Problem,
Mathematics of Computation, Vol. 32, No. 144, Oct. 1978, Pgs. 1281-1291.
(2) J. L. Simons, On the Nonexistence of 2-cycles for the 3n+1 Problem,
Mathematics of Computation, Dec. 8, 2004, Vol. 74, No. 251, pgs. 1565-1572.
(3) J. Simons and B. de Weger, Theoretical and computational bounds for
m-cycles of the 3n+1 problem, Acta Arith. 2005.